Informazioni su questo graficatore di disuguaglianze

Questa calcolatrice vi aiuterà a trovare la soluzione e il grafico di qualsiasi disuguaglianza generale, mostrando tutti i passaggi. È necessario fornire una disuguaglianza valida di una sola variabile (x), digitandola nell'apposita casella.

Ad esempio, è possibile fornire una semplice disuguaglianza lineare come '3x - 1 < 1/3', oppure qualcosa come '2x-x^2 <= 3/4', che corrisponde a una disuguaglianza quadratica.

Una volta indicata la disequazione che si vuole rappresentare, si può cliccare sul pulsante "Risolvi", in modo che vengano presentate le soluzioni, con tutti i passaggi, nel caso in cui sia possibile trovare le soluzioni.

Risolvere equazioni generali e disuguaglianze generali è in generale un compito difficile, tranne che per un insieme specifico di strutture che si prestano a un trattamento sistematico.

Alcuni dei pochi tipi che consentono una soluzione esatta sono disuguaglianze lineari E disuguaglianze polinomiali .

Un tipo importante di disequazioni che vi piacerà risolvere è il caso delle disequazioni razionali, in cui è possibile identificare un quoziente di polinomi. Queste disequazioni sono interessanti perché presentano potenziali divisioni per zero che devono essere affrontate. L'idea di una disequazione razionale può essere facilmente estesa al quoziente di funzioni in generale, non necessariamente polinomiali

Come si fa il grafico di una disuguaglianza

La risposta più semplice è: per poter rappresentare graficamente una disuguaglianza, è necessario sapere come risolverla. La soluzione grafica di una disuguaglianza viene solitamente rappresentata come un intervallo o più intervalli uniti sull'asse delle ascisse.

Quindi, detto questo, il grafico di una disuguaglianza inizia con la sua risoluzione, che consiste nel trovare un insieme di valori sulla retta reale che soddisfino la disuguaglianza fornita.

Si può potenzialmente presentare il grafico come un intervallo a sé stante, oppure si possono tracciare le soluzioni della disequazione insieme al grafico dell'espressione che è alla base della disequazione: ricordiamo che per risolvere disuguaglianze , si passano tutti i termini da una parte (che fornisce l'espressione di base) e si risolve un'equazione ausiliaria

Fasi di risoluzione e rappresentazione grafica delle disuguaglianze

• Passo 1: Passa tutti i termini da un lato, in modo da avere un'espressione da un lato e zero dall'altro
• Passo 2: Dalla disuguaglianza (una volta che tutto è da una parte e zero dall'altra), costruisci un'equazione ausiliaria
• Passaggio 3: Risolvi questa equazione, con un metodo adatto alla sua struttura (diversi tipi di equazioni richiederanno tecniche e approcci specifici)
• Passaggio 4: Sulla base delle soluzioni REALI delle equazioni ausiliarie (reali rispetto a soluzioni complesse), costruisci i tuoi punti critici e ordinali in ordine crescente
• Passaggio 5: È inoltre necessario cercare i punti in cui l'espressione non è definita. Un caso notevole di ciò si verifica con le disuguaglianze razionali, in cui hai un denominatore che è un polinomio, quindi l'espressione sarà indefinita sugli zeri del denominatore. Quindi aggiungi gli zeri del denominatore all'elenco dei punti critici
• Passaggio 6: Con i tuoi punti critici, costruisci intervalli utilizzando punti critici consecutivi (usando -∞ e ∞ come punti critici iniziali e finali)
• Passaggio 7: Per ogni intervallo analizza il segno dell'espressione e verifica se è compatibile con il segno della disuguaglianza. Se lo è, allora l’intervallo farà parte della soluzione complessiva alla disuguaglianza

L'uso dei punti critici per l'analisi è di estrema importanza, perché in questo modo si è sicuri che l'espressione non cambi segno all'interno di ogni intervallo, in modo che il problema si riduca a valutare se la disuguaglianza è risolta per ognuno di questi intervalli critici.

Per renderlo un po' più tangibile, si ha una disuguaglianza data e poi si passa tutto da una parte, in modo da avere qualcosa della forma \(f(x) \le 0\). Ad esempio, potrebbe essere qualcosa come \(x^2 - x + 1 \le 0\).

Quindi si prende \(f(x) \le 0\) e si trova l'equazione ausiliaria \(f(x) = 0\). Si prende l'espressione \(f(x)\) e si trovano i suoi zeri come punti critici. Ma non basta fare questo, bisogna anche vedere se \(f(x)\) è indefinito da qualche parte (divisioni per zero, ecc.). Forse è definita ovunque, come nel caso di \(x^2 - x + 1\), ma se si trovano punti in cui l'espressione è indefinita, li si aggiunge all'elenco dei punti critici.

Quindi si costruiscono intervalli basati su punti critici consecutivi. Per la disequazione \(f(x) \le 0\), si prenderanno come parte delle soluzioni gli intervalli in cui il valore dell'espressione è negativo. Se la disequazione originale fosse stata \(f(x) \ge 0\), si prenderanno come parte delle soluzioni gli intervalli in cui il valore dell'espressione è positivo

Come funziona questo grafico della disuguaglianza

La nostra calcolatrice di disuguaglianze online si occuperà di uno dei processi più complicati dell'algebra di base, ovvero trovare le soluzioni di una disuguaglianza e tracciarne il grafico. Un grande vantaggio della nostra calcolatrice è che mostra tutti i passaggi, quando possibile.

In primo luogo, il grapher risolve la disuguaglianza risolvendo prima un'equazione ausiliaria adatta. Questo processo richiede l'individuazione di specifiche strutture note, poiché tutte le strutture richiedono probabilmente approcci diversi. Ad esempio, per risolvere una disequazione razionale (che coinvolge il quoziente di due polinomi), come ad esempio

\[\displaystyle \frac{x^2-2x}{x-1} \ge 4 \]

si richiederà un approccio diverso da quello utilizzato per risolvere una disuguaglianza quadratica come \(x^2 + 3x < 1\), ad esempio, e questa calcolatrice si occuperà di tutti questi dettagli

Se non viene individuata alcuna struttura tradizionale o comunemente conosciuta, verranno utilizzate diverse sostituzioni comunemente utilizzate, come ad esempio \(u = \sqrt x\) o \(u = \sin x\). Se non funziona nulla, il calcolatore cercherà di trovare le soluzioni per ispezione e per via numerica, in modo da avere almeno un'idea delle soluzioni.

Come si presenta un grafico di disuguaglianza?

Come abbiamo detto sopra, non è scritto sulla pietra, ma il modo più comune è quello di graficare l'espressione sottostante della disuguaglianza ed evidenziare i valori di x che soddisfano la disuguaglianza. Questo è forse il formato grafico migliore ed è quello utilizzato da questo grafico.

È anche possibile disegnare un oggetto intervallo indipendente, ma questo è forse meno significativo, in quanto perde la prospettiva di ciò che sta effettivamente accadendo con la disuguaglianza stessa.

Esempio: grafico delle disuguaglianze

Tracciare il grafico della seguente disuguaglianza: \(\frac{1}{x}+x > 1\)

Soluzione: Ci viene data la seguente disuguaglianza che deve essere risolta:

\[\frac{1}{x}+x > 1\]

Dobbiamo mettere da parte tutti i termini della disuguaglianza:

\[x+\frac{1}{x}-1>0\]

Risoluzione dell'equazione ausiliaria

Dalla disuguaglianza di cui sopra, si ottiene l'equazione associata che deve essere risolta per prima:

\[x+\frac{1}{x}-1=0\]

Analisi dei punti critici

Dobbiamo organizzare i punti critici trovati (dalle radici reali del numeratore e del denominatore) in ordine crescente, definire intervalli con tutti i punti critici consecutivi e valutare il segno della dimensione sinistra della disuguaglianza su ciascuno di questi intervalli.

L'unico punto critico trovato è \(0\).

Su questa base, dobbiamo analizzare i seguenti intervalli:

- Per l'intervallo \(\left(-\infty, 0\right)\): il numeratore è positivo e il denominatore è negativo, quindi il lato sinistro è negativo, il che implica che \(\left(-\infty, 0\right)\) non fa parte della soluzione.

- Per l'intervallo \(\left(0, \infty\right)\): il numeratore è positivo e il denominatore è positivo, quindi il lato sinistro è positivo, quindi \(\left(0, \infty\right)\) fa parte della soluzione.

Soluzione alla disuguaglianza

Sulla base della disuguaglianza fornita e analizzando i punti critici, troviamo che la soluzione della disuguaglianza è: \(x > 0\).

Utilizzando la notazione per intervalli, la soluzione si scrive come:

\[\left(0,\infty\right)\]

Il seguente risultato è stato ottenuto con il grapher delle disuguaglianze:

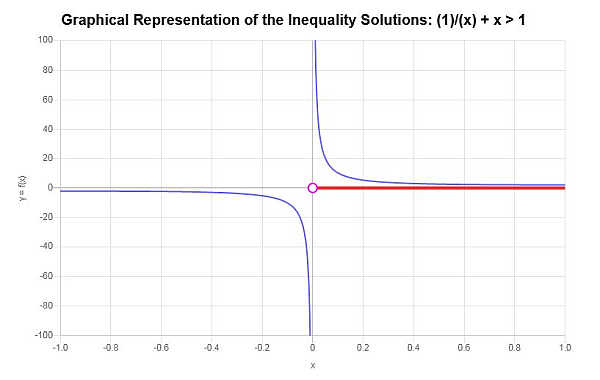
che conclude il calcolo.

Esempio: grafici di disuguaglianze polinomiali

Trovare il grafico della disuguaglianza: \(x^2 - 2x \ge 4\)

Soluzione:

Dobbiamo mettere da parte tutti i termini della disuguaglianza:

\[x^2-2x-4\ge0\]

Risoluzione dell'equazione ausiliaria

Dalla disuguaglianza di cui sopra, si ottiene l'equazione associata che deve essere risolta per prima:

\[x^2-2x-4=0\]

Usando la formula quadratica

Per un'equazione quadratica della forma \(a x^2 + bx + c = 0\), le radici vengono calcolate utilizzando la seguente formula:

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a}\]

In questo caso, abbiamo che l'equazione da risolvere è \(\displaystyle x^2-2x-4 = 0\), il che implica che i coefficienti corrispondenti sono:

\[a = 1\] \[b = -2\] \[c = -4\]

Innanzitutto, calcoleremo il discriminante per valutare la natura delle radici. La discriminante è calcolata come:

\[\Delta = b^2 - 4ac = \displaystyle \left( -2\right)^2 - 4 \cdot \left(1\right)\cdot \left(-4\right) = 20\]

Poiché in questo caso otteniamo che il discriminante è \(\Delta = \displaystyle 20 > 0\), che è positivo, sappiamo che l'equazione ha due radici reali diverse.

Ora, inserendo questi valori nella formula per le radici otteniamo:

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a} = \displaystyle \frac{2 \pm \sqrt{\left(-2\right)^2-4\left(1\right)\left(-4\right)}}{2\cdot 1} = \displaystyle \frac{2 \pm \sqrt{20}}{2}\]

allora, troviamo che:

\[ {x}_1 = \frac{2}{2}-\frac{1}{2}\sqrt{20}=\frac{2}{2}-\sqrt{5}=1-\sqrt{5}=-\sqrt{5}+1 \] \[{x}_2 = \frac{2}{2}+\frac{1}{2}\sqrt{20}=\frac{2}{2}+\sqrt{5}=1+\sqrt{5}=\sqrt{5}+1\]

In questo caso, l'equazione quadratica \( \displaystyle x^2-2x-4 = 0 \), ha due radici reali, quindi:

\[\displaystyle x^2-2x-4 = \left(x+\sqrt{5}-1\right)\left(x-\sqrt{5}-1\right)\]

quindi il polinomio originale viene scomposto come \(\displaystyle p(x) = x^2-2x-4 = \left(x+\sqrt{5}-1\right)\left(x-\sqrt{5}-1\right) \), che completa la fattorizzazione.

Analisi dei punti critici

L'elenco dei punti critici trovati è organizzato in ordine crescente: \(-\sqrt{5}+1\), \(\sqrt{5}+1\).

Su questa base, dobbiamo analizzare i seguenti intervalli:

- Per l'intervallo \(\left(-\infty, -\sqrt{5}+1\right)\): il lato sinistro è positivo, quindi \(\left(-\infty, -\sqrt{5}+1\right)\) fa parte della soluzione.

- Per l'intervallo \(\left(-\sqrt{5}+1, \sqrt{5}+1\right)\): il lato sinistro è negativo, quindi \(\left(-\sqrt{5}+1, \sqrt{5}+1\right)\) non fa parte della soluzione.

- Per l'intervallo \(\left(\sqrt{5}+1, \infty\right)\): il lato sinistro è positivo, il che implica che \(\left(\sqrt{5}+1, \infty\right)\) fa parte della soluzione.

Soluzione alla disuguaglianza

In base alla disuguaglianza fornita e analizzando i punti critici, troviamo che la soluzione della disuguaglianza è: \(x \le -\sqrt{5}+1\) o \(x \ge \sqrt{5}+1\).

Utilizzando la notazione per intervalli, la soluzione si scrive come:

\[\left(-\infty,-\sqrt{5}+1\right] \cup \left[\sqrt{5}+1,\infty\right)\]

Graficamente:

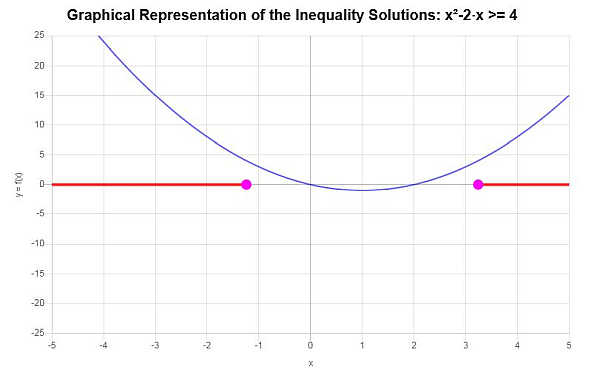
che conclude il calcolo.

Altri calcolatori di algebra

Man mano che si procede nell'apprendimento dell'Algebra e del Calcolo, ci si è probabilmente resi conto che Risolvere le equazioni giocano un ruolo fondamentale. E man mano che si impara, ci si rende conto che a volte abbiamo meno informazioni e finiamo per affrontare il problema del Risolvere le disuguaglianze .

In sostanza, la risoluzione delle disuguaglianze non è più difficile di quella delle equazioni, ma richiede solo qualche passo più organizzato. Il problema principale è che non possiamo risolvere la maggior parte delle equazioni, almeno in modo esatto.

E anche se risolviamo le equazioni numericamente, non disponiamo ancora di modi validi per assicurarci di aver trovato TUTTE le soluzioni a tutte le equazioni possibili. Alcune equazioni degne di nota che possono essere risolte e che compaiono continuamente nelle applicazioni sono le seguenti equazioni polinomiali che si può risolvere con i metodi più comuni (ma solo per polinomi di grado inferiore)

Uno dei tipi di disuguaglianze più comunemente richiesti che devi risolvere nei tuoi test di matematica sono le disuguaglianze razionali, perché sono le disuguaglianze semplici più difficili per le quali puoi garantire di trovare una soluzione (a condizione che i gradi coinvolti siano sufficientemente bassi, o i polinomi sono abbastanza semplici).