Calculatrice d'équations de radicaux
Instructions : Utilisez cette calculatrice d'équations de radicaux pour résoudre toute équation impliquant des radicaux que vous fournissez, en montrant toutes les étapes du processus. Veuillez saisir l'équation de radicaux que vous souhaitez résoudre dans le champ ci-dessous.
Résolution d'équations radicales
Ce résolveur d'équations radicales vous permet de traiter les équations radicales que vous fournissez, en les manipulant algébriquement tout en vous montrant toutes les étapes du processus.
Ce solveur accepte toute équation valide impliquant des racines, qu'il s'agisse d'une équation très simple comme "sqrt(x) = 1" ou d'une équation beaucoup plus difficile à résoudre comme "sqrt(x+3) = x^2 - 1".
Une fois qu'une équation de radicaux valide a été fournie, vous avez pratiquement terminé et tout ce qu'il vous reste à faire est de cliquer sur "Solve" pour obtenir toutes les étapes du processus indiqué.
La solution de l'équation des radicaux s'appuie fortement sur l'efficacité des systèmes d'information et de communication manipulation algébrique de l'expression afin de se débarrasser de la partie radicale.

Qu'est-ce que l'équation radicale ?
Une équation de radicaux, en termes extrêmement simples, est un type d'équation de radicaux équation mathématique dans laquelle l'inconnue (généralement x) se trouve à l'intérieur d'un radical. Par exemple
\[\displaystyle \sqrt x = x^2 \]est une équation radicale, à cause du terme \( \sqrt x\), mais l'équation
\[\displaystyle 2 x = x^2 \]par exemple, n'est PAS une équation de radicaux, parce qu'il n'y a pas d'insider de radical dans l'équation.
Comment résoudre les équations radicales
Résoudre des équations de radicaux n'est pas difficile si vous suivez les étapes suivantes :
- Étape 1 : Tout d'abord, assurez-vous qu'il s'agit bien d'une équation à radicaux. Un autre type d'équation sera probablement résolu différemment
- Étape 2 : Simplifier et regrouper les radicaux autant que possible, l'idéal étant que tout soit concentré dans un seul radical
- Étape 3 : Appliquez une puissance (généralement une puissance de 2) pour éliminer les radicaux. Si vous vous y êtes bien pris et que l'équation peut être résolue, vous réduirez l'équation d'origine à une Equation polynomiale .
- Étape 4 : Résoudre la fonction auxiliaire et vérifier laquelle des solutions auxiliaires (s'il y en a) est une solution à l'équation originale
Parfois, malgré un regroupement et une simplification appropriés, il ne sera pas possible d'éliminer complètement les radicaux, ou cela conduira à une équation encore plus compliquée.
Simplification des équations radicales
Comme nous l'avons mentionné plus haut, la réussite du calcul d'équations impliquant des racines dépend fortement de la capacité à simplifier les radicaux . Mais parfois, cela ne suffit pas, car la simplification de tous les radicaux ne les fera pas disparaître. La méthode la plus courante consiste à réduire les radicaux, puis à appliquer le carré (puissance de 2) pour annuler le radical.
Mais la mise au carré pour se débarrasser du radical est une arme à double tranchant, car en mettant au carré, tout signe pertinent peut disparaître. C'est pourquoi, lorsque l'on "élimine" le radical et que l'on trouve les solutions d'une équation auxiliaire, il FAUT vérifier que les solutions auxiliaires sont également des solutions de l'équation originale. Souvent, ce n'est pas le cas.

Une autre façon de voir le processus d'élimination du radical est d'utiliser une substitution appropriée. Par exemple, pour l'équation du radical :
\[\displaystyle \sqrt x = x \]vous pouvez définir \(u = \sqrt x\), puis \(u^2 = (\sqrt x)^2 = x\), de sorte que l'équation originale se transforme en l'équation auxiliaire suivante :
\[\displaystyle \sqrt x = x \Rightarrow u = u^2\]qui est une équation polynomiale que nous pouvons résoudre. Ainsi, l'utilisation d'une substitution permet de passer d'une équation que l'on ne sait pas résoudre à résolution d'une équation polynomiale que nous savons qui résoudre.
Pourquoi s'intéresser aux équations de radicaux ?
Les équations radicales apparaissent fréquemment en algèbre et en calcul, car elles sont à la base de la modélisation d'un grand nombre de phénomènes différents.
Les fonctions radicales sont intéressantes en raison de leurs propriétés et de leur type de croissance lente lorsque x s'approche de l'infini.

Exemple : résolution d'équations impliquant un radical
Résolvez la question suivante : \(\sqrt{x} = 2x\)
Solution :
L'équation suivante nous est fournie. Nous devons résoudre cette équation qui n'a qu'une seule variable, \(x\), et l'objectif est donc de trouver \(x\) :
\[\sqrt{x}=x^2\]Observez que le degré du polynôme donné est \(\displaystyle deg(p) = 4\), son coefficient directeur est \(\displaystyle a_{4} = -1\) et son coefficient constant est \(\displaystyle a_0 = 0\).
Tentative de racines rationnelles
Candidats Aux Racines Rationnelles : Puisque le premier terme avec un coefficient non nul dans \(p(x)\) est \(x\), nous pouvons factoriser ce terme pour obtenir
\[\displaystyle p(x) = -x^4+x = x \left(-x^3+1 \right) \]mais le terme entre parenthèses a un degré supérieur à 2, il n'y a donc pas de formule élémentaire pour le factoriser. Nous devons tester les éventuelles racines rationnelles.
La tâche suivante consiste à trouver les nombres entiers qui divisent le coefficient principal \(a_{3}\) et le coefficient constant \(a_0\), qui seront utilisés pour construire nos candidats aux zéros de l'équation polynomiale.
les diviseurs de \(a_{3} = -1\) sont : \(\pm 1\).
les diviseurs de \(a_0 = 1\) sont : \(\pm 1\).
Par conséquent, en divisant chaque diviseur du coefficient constant \(a_0 = 1\) par chaque diviseur du coefficient directeur \(a_{3} = -1\), nous trouvons la liste suivante de candidats à être des racines :
\[\pm \frac{ 1}{ 1}\]Maintenant, tous les candidats doivent être testés pour voir s'ils constituent une solution. Les résultats suivants sont obtenus en testant chaque candidat :
\[\begin{array}{ccccclcc} x & = & \displaystyle -1 &:& & \displaystyle -\left(-1^3\right)+1 & = & \displaystyle 2 \ne 0 \\\\ x & = & \displaystyle 1 &:& & \displaystyle -1^3+1 & = & \displaystyle 0 \\\\ \end{array}\]Division Polynomiale : Comme nous n'avons pas assez de racines parmi les candidats rationnels, nous allons diviser \(\displaystyle -x^3+1\) par le produit des facteurs dérivés des racines rationnelles, soit \(\displaystyle \left(x-1\right) \).
Étape 1 : Le premier terme du dividende \(\displaystyle p(x) = -x^3+1\) est \(\displaystyle -x^3\), tandis que le premier terme du diviseur \(\displaystyle s(x) = x-1\) est égal à \(\displaystyle x\).
Ainsi, le terme que nous devons multiplier par \(x\) pour obtenir le premier terme du dividende est \(\displaystyle \frac{ -x^3}{ x} = -x^2\), nous ajoutons donc ce terme au quotient. Nous le multiplions également par le diviseur pour obtenir \(\displaystyle -x^2 \cdot \left(x-1\right) = -x^3+x^2\), que nous devons soustraire au dividende :
\[\def\arraystretch{1.5}\begin{array}{rcccc} &\displaystyle -x^2 & \displaystyle & \displaystyle &\\[0.3em] \hline x-1\,) & \displaystyle -x^3 & \displaystyle & \displaystyle & \displaystyle +1\\[0.3em] \displaystyle &\displaystyle x^3 & \displaystyle -x^2 & \displaystyle & \displaystyle \\[0.3em] \hline \displaystyle &\displaystyle & \displaystyle -x^2 & \displaystyle & \displaystyle +1\\[0.3em] \end{array}\]Étape 2 : Maintenant, le premier terme du reste actuel \(\displaystyle -x^2+1\) est \(\displaystyle -x^2\), et nous savons que le premier terme du diviseur est \(\displaystyle x\).
Ainsi, le terme que nous devons multiplier par \(x\) pour obtenir le premier terme du reste actuel est \(\displaystyle \frac{ -x^2}{ x} = -x\), nous ajoutons donc ce terme au quotient. Nous le multiplions également par le diviseur pour obtenir \(\displaystyle -x \cdot \left(x-1\right) = -x^2+x\), que nous devons soustraire au reste actuel :
\[\def\arraystretch{1.5}\begin{array}{rcccc} &\displaystyle -x^2 & \displaystyle -x & \displaystyle &\\[0.3em] \hline x-1\,) & \displaystyle -x^3 & \displaystyle & \displaystyle & \displaystyle +1\\[0.3em] \displaystyle &\displaystyle x^3 & \displaystyle -x^2 & \displaystyle & \displaystyle \\[0.3em] \hline \displaystyle &\displaystyle & \displaystyle -x^2 & \displaystyle & \displaystyle +1\\[0.3em] \displaystyle &\displaystyle & \displaystyle x^2 & \displaystyle -x & \displaystyle \\[0.3em] \hline \displaystyle &\displaystyle & \displaystyle & \displaystyle -x & \displaystyle +1\\[0.3em] \end{array}\]Étape 3 : Maintenant, le premier terme du reste actuel \(\displaystyle -x+1\) est \(\displaystyle -x\), et nous savons que le premier terme du diviseur est \(\displaystyle x\).
Ainsi, le terme que nous devons multiplier par \(x\) pour obtenir le premier terme du reste actuel est \(\displaystyle \frac{ -x}{ x} = -1\), nous ajoutons donc ce terme au quotient. Nous le multiplions également par le diviseur pour obtenir \(\displaystyle -1 \cdot \left(x-1\right) = -x+1\), que nous devons soustraire au reste actuel :
\[\def\arraystretch{1.5}\begin{array}{rcccc} &\displaystyle -x^2 & \displaystyle -x & \displaystyle -1&\\[0.3em] \hline x-1\,) & \displaystyle -x^3 & \displaystyle & \displaystyle & \displaystyle +1\\[0.3em] \displaystyle &\displaystyle x^3 & \displaystyle -x^2 & \displaystyle & \displaystyle \\[0.3em] \hline \displaystyle &\displaystyle & \displaystyle -x^2 & \displaystyle & \displaystyle +1\\[0.3em] \displaystyle &\displaystyle & \displaystyle x^2 & \displaystyle -x & \displaystyle \\[0.3em] \hline \displaystyle &\displaystyle & \displaystyle & \displaystyle -x & \displaystyle +1\\[0.3em] \displaystyle &\displaystyle & \displaystyle & \displaystyle x & \displaystyle -1\\[0.3em] \hline \displaystyle & & & & 0\\[0.3em] \end{array}\]Par conséquent, le quotient est \(\displaystyle q(x) = -x^2-x-1\), et le reste est \(\displaystyle r(x) = 0\).
Donc après avoir divisé, nous avons avancé dans la factorisation avec
\[\displaystyle p(x) = -x^4+x = - x \left(x-1\right) \left(-x^2-x-1\right)\]Mais maintenant, puisque le quotient trouvé \(\displaystyle -x^2-x-1\) est quadratique, nous pouvons trouver ses racines pour voir si nous pouvons le factoriser sur le corps réel.
Nous devons résoudre l'équation quadratique suivante \(\displaystyle -x^2-x-1=0\).
Utilisation de la formule quadratique
Pour une équation quadratique de la forme \(a x^2 + bx + c = 0\), les racines sont calculées à l'aide de la formule suivante :
\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a}\]Dans ce cas, l'équation à résoudre est \(\displaystyle -x^2-x-1 = 0\), ce qui implique que les coefficients correspondants sont :
\[a = -1\] \[b = -1\] \[c = -1\]Tout d'abord, nous allons calculer le discriminant pour évaluer la nature des racines. Le discriminant est calculé comme suit :
Puisque dans ce cas le discriminant est \(\Delta = \displaystyle -3 < 0\), qui est négatif, nous savons que l'équation donnée a deux racines complexes conjuguées différentes.
En introduisant ces valeurs dans la formule des racines, nous obtenons :
\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a} = \displaystyle \frac{1 \pm \sqrt{\left(-1\right)^2-4\left(-1\right)\left(-1\right)}}{2\cdot -1} = \displaystyle \frac{1 \pm \sqrt{-3}}{-2}\]donc, nous trouvons que :
\[\displaystyle {x}_1 = \frac{1 - i \sqrt{3}}{-2} = -\frac{1}{2}+\frac{1}{2}\sqrt{3}i\] \[\displaystyle {x}_2 = \frac{1 + i \sqrt{3}}{-2} = -\frac{1}{2}-\frac{1}{2}\sqrt{3}i\]Ainsi, après avoir trouvé les racines de la dernière partie quadratique, nous trouvons deux racines complexes, de sorte que nous ne pouvons pas factoriser le terme \(-x^2-x-1\) dans le domaine réel, et nous terminons donc le processus avec \(\displaystyle p(x) = -x^4+x = - x \left(x-1\right) \left(-x^2-x-1\right)\).
Conclusion : Par conséquent, la factorisation finale que nous obtenons est :
\[\displaystyle p(x) = -x^4+x = - x\left(x-1\right)\left(-x^2-x-1\right)\]Les racines trouvées en utilisant le processus de factorisation sont \(0\), \(1\), \(-\frac{1}{2}+\frac{1}{2}\sqrt{3}i\), et \(-\frac{1}{2}-\frac{1}{2}\sqrt{3}i\) .
Par conséquent, la résolution de \(x\) pour l'équation polynomiale donnée conduit aux solutions \(x = \, \)\(0\), \(1\), \(-\frac{1}{2}+\frac{1}{2}\sqrt{3}i\), \(-\frac{1}{2}-\frac{1}{2}\sqrt{3}i\), en utilisant les méthodes de factorisation.
Vérification des solutions auxiliaires
Le test de ces solutions à partir de l'équation polynomiale auxiliaire montre que toutes les solutions candidates ne sont pas en fait une solution de l'équation originale. Les seules solutions réelles de l'équation originale sont les suivantes :
\[x_1=0 \]\[x_2=1 \]
Par conséquent, la résolution de \(x\) pour l'équation donnée conduit aux solutions \(x=0,\,\,x=1\).
Graphiquement
La représentation graphique des solutions obtenues est la suivante :
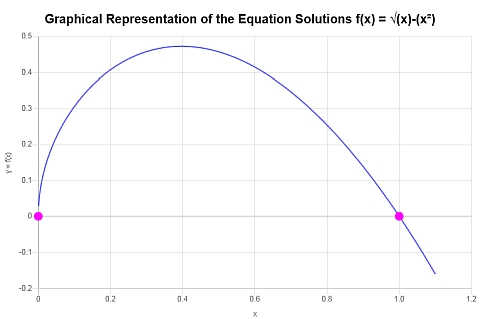
qui conclut le calcul.
Autres résolveurs d'équations utiles
Lors de la résolution d'équations de radicaux, contrairement au cas où vous devez Résoudre des équations linéaires ou lorsque vous devez résoudre une équation quadratique appartient à la catégorie des équations qui nécessitent une manipulation algébrique astucieuse afin de résoudre x.
En d'autres termes, il n'y aura pas de solution du type "faites comme ça et ça marchera toujours". Le type de manipulation que vous effectuerez dépendra de la structure de l'équation et peut varier considérablement d'un cas à l'autre.
simplifier les expressions est toujours une bonne pratique, car elle permet de réduire les termes qui peuvent encombrer la structure globale de l'équation.



