Álgebra Tutoriales

Encontrar el gráfico de registro

La forma de encontrar el gráfico logarítmico es común a todas las funciones logarítmicas. Esto se debe a que todas las funciones logarítmicas tienen esencialmente la misma forma, al menos estructuralmente, solo depende de la base del logaritmo.

Primero, recordemos la función logarítmica con base \(a\), \(\log_a x\). Las bases más típicas que se utilizan son para \(a = 10\), en cuyo caso escribimos simplemente \(\log x\), y el caso donde \(a = e\), en cuyo caso escribimos \(\ln x\), y lo llamamos el registro natural.

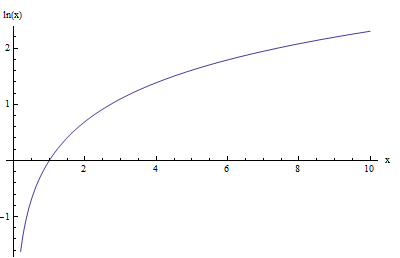
Por ejemplo, el gráfico de la función logarítmica natural, \(\ln x\) se muestra a continuación:

Ahora, veamos qué sucede cuando graficamos juntos \(\log x\) y \(\ln x\) (este es el registro base 10 y el registro natural):

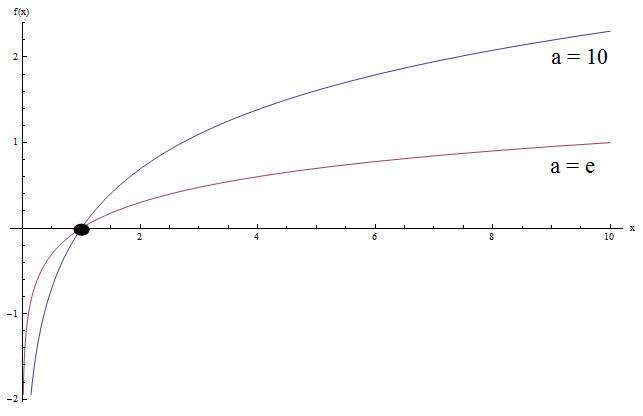
¿Ves alguna similitud? Bueno, hay algunos.

Observe que ambas gráficas tienen la misma forma cóncava general. Además, ambas gráficas cruzan el eje y en \(x = 1\) (lo cual no es una sorpresa ya que \(\log_a 1 = 0\) para todas las bases, con \(a > 0\)).

Otra cosa es que ambos gráficos se acercan al infinito negativo cuando \(x\) se acerca a 0, y al infinito cuando \(x\) se acerca al infinito.

¿Qué pasa si intentamos graficar funciones logarítmicas con \(0 < a < 1\) ?. Mira el ejemplo a continuación:

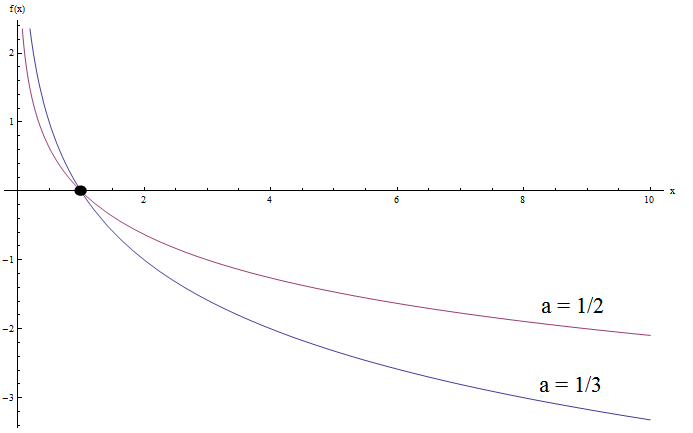
Funciones de registro con base inferior a 1

¿Ves alguna similitud ahora? Por supuesto.

Observe que ambas gráficas tienen la misma forma convexa general. Además, ambas gráficas vuelven a cruzar el eje y en \(x = 1\), que es lo esperado.

Pero ahora ambos gráficos se acercan al infinito cuando \(x\) se acerca a 0, y al infinito negativo cuando \(x\) se acerca al infinito. Es una especie de comportamiento opuesto a cuando la base \(a\) es mayor que 1.

¿Cómo se hace un gráfico logarítmico?

Basándonos en lo que encontramos en los ejemplos anteriores, podemos incluir algunas reglas que puede usar cuando desee hacer gráficos de registro:

Suponga que desea graficar la función \(y = \log_a x\), para \(a > 0\). Luego:

Paso 1 : SIEMPRE, la función logarítmica cruza el eje y en \(x = 1\).

Paso 2 : Si \(a > 1\), entonces el gráfico es creciente y cóncavo. También:

\[\lim_{x\to 0^+} \log_a x = -\infty, \,\, \lim_{x\to \infty} \log_a x = \infty\]

Paso 3 : Si \(0 < a < 1\), entonces la gráfica es decreciente y convexa. También:

\[\lim_{x\to 0^+} \log_a x = \infty, \,\, \lim_{x\to \infty} \log_a x = -\infty\]

Fácil, ¿verdad?

Más acerca de los gráficos de registro

Primero que todo, saber cómo graficar una función es una habilidad crucial, considerando que la gráfica de una función te da MUCHA información al respecto.

En las secciones anteriores aprendimos cómo la base de un registro afecta el gráfico. Lo interesante es que la forma y el comportamiento del gráfico logarítmico depende solo de si \(a > 1\) y \(0 < a < 1\).

¿Puede un registro ser igual a un número negativo?

Bueno, tenemos que especificar qué queremos decir con eso. Primero, la base de la función logarítmica no puede ser negativa. Además, el argumento de una función logarítmica tampoco puede ser negativo.

PERO, el logaritmo de un número puede ser absolutamente negativo. Por ejemplo: \(\ln(1/e) = -1\).

¿Cómo grafica las funciones logarítmicas inversas?

Bueno, lo primero que debe saber es que la inversa de una función logarítmica siempre será una función exponencial.

Entonces, graficar la inversa de una función logarítmica es tan fácil como saber cuál es la exponencial correspondiente y graficarla.

También hay otros métodos. Puede dibujar el gráfico logarítmico original y dibujar un gráfico que sea simétrico a este gráfico logarítmico dado, con respecto a los 45 ^o línea recta \(y = x\).

O use el gráfico original y cambie el valor de \(x\) por el valor de \(y\).

Este tutorial está orientado a las propiedades gráficas de la función logarítmica. Para el definición y reglas básicas de registro, verifique esta .