Ecuaciones literales
Las ecuaciones literales son ecuaciones donde hay símbolos que no son variables, pero representan una constante. Entonces es como una ecuación, pero algunos de los números en lugar de ser números se expresan como constantes genéricas.
En este tutorial, aprenderá cómo manejar ecuaciones literales y cómo operar con ellas.
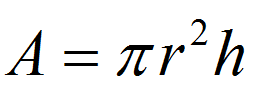
¿Qué es una ecuación literal?
La primera tarea que tenemos a mano es especificar qué es una ecuación literal. Cuando decimos "literal", nos referimos a "letras". Sí, del latín literal proviene de "letras"
Entonces, una ecuación literal es una ecuación que involucra muchas "letras", a diferencia de números. Se supone que esas letras no son variables, se supone que representan números, en términos de una constante genérica.
Por lo tanto, para identificar una ecuación literal, debemos ver muchas letras, de las cuales una (o potencialmente más) es la real.
variable
.
Como en cualquier otra ecuación, la idea es resolver para la variable (lo que significa aislar la variable en un lado de la ecuación).
Por ejemplo, considere la fórmula para volumen de un cilindro de radio \(r\) y altura \(h\):
\[V = \pi r^2 h\]Esta es una ecuación literal. ¿Por qué? Porque tenemos una ecuación con muchas letras.
La pregunta es qué es la variable y cuáles son las constantes. En verdad, eso es subjetivo, hasta cierto punto.
Por ejemplo, se podría argumentar que \(V\) es la variable, y \(r\) y \(h\) son los literales (o constantes), y tendría sentido.
Pero se podría decir que, por ejemplo, se nos da el volumen \(V\) y la altura \(h\), y necesitas encontrar el radio \(r\). En ese caso tenemos la misma ecuación literal, pero la variable sería \(r\).
Es relevante saber cuál es la variable en una ecuación literal, para saber qué estamos resolviendo.
Estrategias para lidiar con una ecuación literal
Entonces, tenemos una ecuación literal, ¿ahora qué? Bueno, como cualquier otra ecuación, deberíamos intentar resolverla.
Esto significa que necesitamos aislar la variable en un lado de la ecuación y poner todo lo demás, usando todas las reglas algebraicas disponibles, en el otro lado.
Esto significa, en términos prácticos, que estamos expresando la variable en términos (o como una función) de las constantes (literales).
El proceso de resolver ecuaciones literales es el mismo que el de resolver ecuaciones regulares:
Sumamos, restamos, multiplicamos o dividimos términos en ambos lados de la igualdad para aislar la variable.
No hay una forma de hacer la solución, depende de las características y la estructura de la ecuación.
Ejemplos de resolución de ecuaciones literales
La forma más rápida de aprender una habilidad en matemáticas es PRACTICAR. Aquí vamos.
EJEMPLO 1:
Volvamos al ejemplo del cilindro. Para un cilindro con volumen dado \(V\) y altura \(h\), encuentre su radio \(r\)
RESPONDER:
Sabemos que la fórmula para el volumen de un cilindro es
\[\large V = \pi r^2 h\]Para la ecuación literal anterior, tenemos que la variable (la que queremos resolver) es \(r\) y las constantes (valores dados) son \(V\) y \(h\).
El proceso de resolución de \(r\) se muestra a continuación:
\[\large V = \pi r^2 h\] \[\large \displaystyle \Rightarrow \frac{V}{\pi h} = r^2\] \[\large \displaystyle \Rightarrow \sqrt{\frac{V}{\pi h}} = r\]Por tanto, la ecuación literal está resuelta, porque tenemos \(r\) aislado en un lado de la igualdad y el resto en el otro lado.
EJEMPLO 2:
Resuelve la siguiente ecuación literal:
\[\large m n = \frac{x-y}{k} \]para \(x\).
RESPONDER:
En este caso, se nos dice explícitamente que la variable es \(x\), por lo que todas las demás letras son constantes a los efectos de resolver la ecuación.
Se obtiene lo siguiente al resolver para \(x\):
\[\large m n = \displaystyle \frac{x-y}{k} \] \[\large m n k = x-y \] \[\large m n k+y = x \]que finaliza el cálculo.
Más sobre la resolución de ecuaciones literales
¿Por qué hablamos de la diferencia entre ecuaciones literales y ecuaciones regulares? En realidad, no hacemos ruido. Una ecuación literal es una ecuación, ante todo.
El ejercicio conceptual consiste en darnos cuenta de que, independientemente de que tengamos un número o una constante que represente un número genérico, el proceso de resolver la ecuación es idéntico. Ese es el concepto clave.
Cómo resolver ecuaciones literales con fracciones
Entonces, ¿qué sucede si encuentra fracciones cuando resuelve una ecuación literal con fracciones? Bueno, lo mismo que harías con una ecuación regular: si quieres eliminar algo que está en el denominador, multiplicas ambos lados de la ecuación por él, y si quieres eliminar algo que está en el numerador, divides ambos lados de la ecuación por él.
¿Existe alguna estrategia que funcione mejor?
Realmente no. Dependiendo del tipo de ecuación que tenga, puede utilizar algunas estrategias específicas para facilitar su trabajo. Por ejemplo, si tiene un ecuación logarítmica (una ecuación en la que la variable está dentro de un logaritmo), es mejor hacer un uso eficiente de la reglas de registro para resolver esas ecuaciones de manera eficiente.