Calculadora de prueba z de dos medias

Esta calculadora permite ejecutar una prueba z para dos medias, mostrando todos los pasos. La prueba z es muy similar a una prueba t , pero con una clara diferencia que para el caso de un Prueba Z necesitamos saber la desviación estándar de la población correspondiente.

Para esta prueba, debe proporcionar dos muestras, más la desviación estándar de la población correspondiente para cada grupo. Quizás se pregunte qué sucede si no tengo esas desviaciones estándar de población: la respuesta es simple: entonces NO PUEDE ejecutar la prueba z para dos medios.

Una vez que haya proporcionado todos los datos requeridos, todo lo que tiene que hacer es hacer clic en "Calcular", y se le mostrarán todos los pasos del proceso.

¿qué es una prueba z de dos muestras?

Una prueba z de dos muestras es un tipo de prueba z que compara las medias de dos grupos. Puede proporcionar los datos de la muestra (junto con las desviaciones estándar de la población), o puede ejecutar un Prueba z para dos medias con datos resumidos , para lo cual debe proporcionar las medias de la muestra en lugar de los datos de la muestra.

Cuál de los dos procesos ejecutará, la prueba z para datos de muestra o para datos resumidos, dependerá en gran medida de la información que tenga disponible.

Prueba z para fórmula de dos medias

Hay una expresión simple para la fórmula utilizada en esta prueba. La fórmula de la prueba z es

\[z = \displaystyle{\frac{\bar X_1 - \bar X_2}{\sqrt{\displaystyle{\frac{\sigma_1^2}{n_1}} + \displaystyle{\frac{\sigma_2^2}{n_2}} }}} \]

La ventaja en este caso es que no necesitamos tratar con grados de libertad, como en el caso del prueba t para dos medias , y con pruebas t en general.

¿cómo hacer una prueba z de 2 muestras en esta calculadora?

• Paso 1: Identifique las muestras que desea comparar. Por lo general, querrá realizar algunos análisis estadísticos descriptivos para asegurarse de que las muestras tengan una forma de campana razonable.
• Paso 2: También debe identificar las desviaciones estándar de la población \(\sigma_1\) y \(\sigma_2\). Si no los tiene, no puede ejecutar una prueba z
• Paso 3: A partir de las muestras, debe encontrar las medias muestrales \(\bar X_1\) y \(\bar X_2\)
• Etapa 4: Ahora, solo ingrese su información en la fórmula \(z = \displaystyle{\frac{\bar X_1 - \bar X_2}{\sqrt{\displaystyle{\frac{\sigma_1^2}{n_1}} + \displaystyle{\frac{\sigma_2^2}{n_2}} }}}\)
• Paso 5: Una vez que tenga la estadística z, a la que llama, \(z_{obs}\), necesita calcular el valor p
• Paso 6: Para las pruebas de cola izquierda, calcula \(p = \Pr(Z < z_{obs})\). Para pruebas de cola derecha, calcula \(p = \Pr(Z > z_{obs})\) y para pruebas de dos colas, calcula \(p = \Pr(|Z| > z_{obs})\)
• Paso 7: Una vez que tiene el valor p, llega a una conclusión basada en el valor elegido del nivel de significancia \(\alpha\): si \(p < \alpha\), rechaza la hipótesis nula, y de lo contrario, no tiene suficiente evidencia para rechazar la nula hipótesis

Un punto importante: si no rechaza la hipótesis nula Ho, eso no significa que acepta la hipótesis nula, simplemente significa que no pudo encontrar suficiente evidencia para rechazarla.

¿en qué se diferencia esto de la prueba z para dos proporciones?

Son similares en el sentido de que ambas son pruebas z, que usan el distribución normal para determinar todas las probabilidades asociadas.

La diferencia es que están midiendo cosas diferentes: la prueba z para dos medias compara las medias de dos grupos, donde estas variables se miden a nivel de intervalo o razón, mientras que la prueba z para dos proporciones comparará la proporción de un cierta característica asociada con los datos.

¿cómo hacer una prueba z de dos muestras en excel?

Excel tiene funciones internas que le permiten ejecutar una prueba z y muchos otros procedimientos, pero no le muestra todos los pasos del proceso como lo hace esta calculadora.

Al final, es posible que pueda obtener una respuesta numérica de Excel u otra calculadora, pero no tendrá los pasos para encontrar la prueba z en una calculadora normal.

Un ejemplo de una prueba z de dos medias

Una instructora está probando un método de enseñanza y obtiene una muestra de 10 estudiantes que se someten a un método y otra muestra de 11 estudiantes que se someten al otro método. Las calificaciones obtenidas después de enseñar usando esos métodos son:

Grupo 1: 89, 78, 90, 100, 90, 92, 90, 80, 89, 93

Grupo 2: 91, 89, 91, 95, 92, 93, 91, 87, 90, 94, 90

Además, sabe que la desviación estándar de la población de las puntuaciones para el primer método es 3,4, mientras que para el segundo es 4,1. ¿Puede el instructor concluir que existe una diferencia significativa entre los métodos? Use un nivel de significancia de .05

Solución:

Se ha proporcionado la siguiente información de muestra:

Muestra 1	Muestra 2
89	91
78	89
90	91
100	95
90	92
92	93
90	91
80	87
89	90
93	94
	90

Para realizar una prueba z de dos muestras independientes, necesitamos calcular estadísticas descriptivas de las muestras:

	Muestra 1	Muestra 2
	89	91
	78	89
	90	91
	100	95
	90	92
	92	93
	90	91
	80	87
	89	90
	93	94
		90
Promedio	89.1	91.1818
norte	10	11

En resumen, se utilizarán los siguientes estadísticos descriptivos en el cálculo del estadístico z:

Se ha proporcionado la siguiente información:

Sample Mean 1 \((\bar X_1)\) =	\(89.1\)
Population Standard Deviation 1\((\sigma_1)\) =	\(3.4\)
Sample Size 1\((n_1)\) =	\(10\)
Sample Mean 2 \((\bar X_2)\) =	\(91.1818\)
Population Standard Deviation 2 \((\sigma_2)\) =	\(4.1\)
Sample Size 2\((n_2)\) =	\(11\)
Significance Level \((\alpha)\)	\(0.05\)

(1) Hipótesis Nula y Alternativa

Se deben probar las siguientes hipótesis nula y alternativa:

\[ \begin{array}{ccl} H_0: \mu_1 & = & \mu_2 \\\\ \\\\ H_a: \mu_1 & \ne & \mu_2 \end{array}\]

Esto corresponde a una prueba de dos colas, y se utilizará una prueba z para dos medias, con desviaciones estándar de población conocidas.

(2) Región De Rechazo

Según la información proporcionada, el nivel de significancia es \(\alpha = 0.05\) y el valor crítico para una prueba de dos colas es \(z_c = 1.96\).

La región de rechazo para esta prueba de dos colas es \(R = \{z: |z| > 1.96\}\)

(3) Estadísticas De Prueba

El estadístico z se calcula de la siguiente manera:

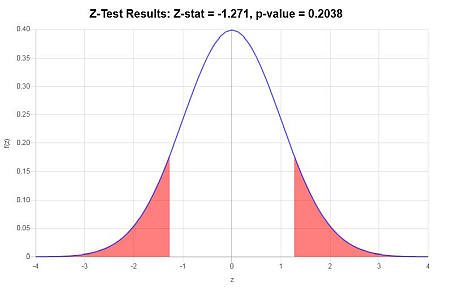
\[ \begin{array}{ccl} z & = & \displaystyle \frac{\bar X_1 - \bar X_2}{\sqrt{ {\sigma_1^2/n_1} + {\sigma_2^2/n_2} }} \\\\ \\\\ & = & \displaystyle \frac{ 89.1 - 91.1818}{\sqrt{ {3.4^2/10} + {4.1^2/11} }} \\\\ \\\\ & = & -1.271 \end{array}\]

(4) Decisión sobre la hipótesis nula

Dado que se observa que \(|z| = 1.271 \le z_c = 1.96\), se concluye que no se rechaza la hipótesis nula.

Usando el enfoque del valor P: El valor p es \(p = 0.2038\), y dado que \(p = 0.2038 \ge 0.05\), se concluye que no se rechaza la hipótesis nula.

(5) Conclusión

Se concluye que la hipótesis nula Ho no es rechazado. Por lo tanto, no hay evidencia suficiente para afirmar que la media poblacional \(\mu_1\) es diferente de \(\mu_2\), en el nivel de significancia \(\alpha = 0.05\).

Intervalo De Confianza

El intervalo de confianza del 95 % para \(\mu_1-\mu_2\) es \(-5.293 < \mu_1 - \mu_2 < 1.129\).

Gráficamente

Más calculadoras de pruebas estadísticas

Estrechamente relacionado con esta calculadora, tienes la calculadora para un Prueba z para dos muestras con datos resumidos , que básicamente realiza el mismo procedimiento, pero recibe el resumen de estadísticas descriptivas ya conocido.

Dentro de la familia de pruebas z , tenemos la prueba z para una media, y la Prueba Z para dos proporciones .

Además, te puede interesar un calculadora de fracciones mixtas , dependiendo de su entorno de aprendizaje. En entornos más elementales, los números mixtos se tratan como entidades importantes, mientras que en entornos más avanzados, los números mixtos solo se presentan en su notación de fracción.