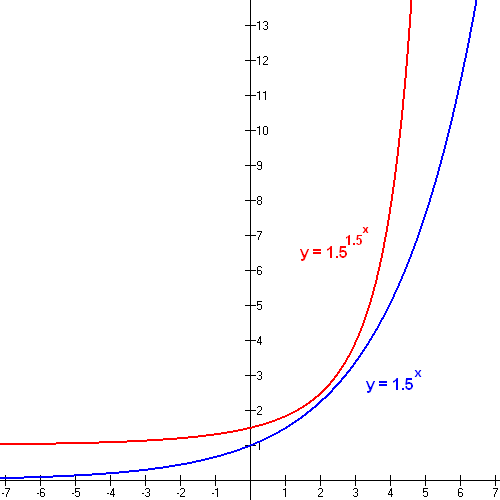
Calculadora de crecimiento exponencial
Instrucciones: Utilice esta calculadora de crecimiento exponencial paso a paso con pasos para encontrar la función que describe el crecimiento exponencial para los parámetros dados. Debe proporcionar el valor inicial \(A_0\), tasa de aumento por período (que puede ser anual o continuo).
La calculadora de crecimiento exponencial
Utilice esta calculadora de crecimiento exponencial para especificar una función que crece proporcionando su valor inicial y su tasa de crecimiento (o tasa de decrecimiento). Para hacer una tasa de crecimiento válida, proporcione una tasa positiva.
Además, tienes la opción de decidir cómo está actuando esta tasa, ya sea anual o continua. Luego hace clic en "Calcular" para obtener todos los pasos que se muestran.
El crecimiento exponencial es un comportamiento algebraico que tiene muchos usos en la vida real, desde las finanzas hasta la economía, desde las ciencias sociales hasta la biología. Representa un crecimiento que se agrava cada período por una determinada tasa (o porcentaje).
Una forma de ver es que el tasa de cambio es proporcional al tamaño de la función.
Fórmula de crecimiento exponencial
Se dice que una función \(f(t)\) tiene un comportamiento de crecimiento exponencial si se puede expresar como:
\[f(t) = A_0 (1 + r)^t \]Para la fórmula anterior, \(r\) corresponde a la tasa de crecimiento, expresada como un número decimal o como un porcentaje (son equivalentes).
Por lo general, se le proporcionará la tasa de crecimiento compuesto y el valor inicial \(A_0\), pero a veces se le proporcionará información sobre la función y tendrá que inferir los parámetros \(r\) y \(A_0\).
Para la fórmula de crecimiento exponencial anterior, hay un caso especial en el que la tasa se capitaliza continuamente, en cuyo caso la fórmula se convierte en
\[f(t) = A_0 e^{rt} \]Típicamente, crecimiento exponencial Las funciones representan dinero, pero como mencionamos antes, pueden representar una variedad de fenómenos, como el crecimiento de la población.
Este tipo de fenómenos se pueden ver reflejados en la curva exponencial, que comienza relativamente plana, pero aumenta rápidamente.
Aplicaciones de crecimiento exponencial
Puedes usar esto Calculadora de función exponencial para diferentes tipos de modelos, siempre que conozca los parámetros que se requieren.
Un modelo típico de este tipo implica poblaciones específicas que crecen rápidamente. Esto puede sucederle a las bacterias, los insectos e incluso a la población humana. Por lo general, a medida que las poblaciones crecen rápidamente, la competencia por los recursos se vuelve más estricta y el crecimiento deja de ser exponencial.
Observe que esta calculadora también le proporcionará la gráfica de la función exponencial resultante.
¿cómo se relacionan el crecimiento exponencial y el decaimiento exponencial?
El crecimiento exponencial y el decaimiento exponencial son absolutamente análogos, y la principal diferencia es que la tasa \(r\) en el crecimiento exponencial es positiva y es negativa en el decaimiento exponencial.
También puedes usar esto Calculadora De Decaimiento Exponencial para el comportamiento exponencial inverso pero análogo, que corresponde al decaimiento exponencial, donde la tasa de crecimiento ahora es negativa.
Entonces, ¿cómo sé si es crecimiento o decadencia? Simple, solo observa la tasa, y si es positiva, entonces tiene crecimiento y si es negativa, entonces tiene decadencia.
Tanto la calculadora de crecimiento exponencial como la de decrecimiento te mostrarán todos los pasos, que esencialmente consisten en resolver dos ecuaciones simultáneas con dos incógnitas.
.Crecimiento exponencial desde dos puntos
Ahora, es posible que desee calcular una función exponencial de dos puntos por donde se sabe que pasa.
Pero, ¿cómo encuentras la tasa de crecimiento exponencial con dos puntos? Empiezas con una ecuación exponencial genérica de la forma \(f(t) = A_0 e^{r t}\). Esta ecuación tiene dos incógnitas que son \(A_0\) y \(k\).
Entonces, reemplazando dos puntos \((t_1, y_1)\) y \((t_2, y_2)\) en \(f(t) = A_0 e^{r t}\), tendrás dos ecuaciones con dos incógnitas, que se podrán resolver siempre que \(t_1 \ne t_2\), lo cual tiene sentido, porque no queremos dos puntos con el misma coordenada x.