So finden Sie die Reichweite
Das Erlernen des Ermittelns des Funktionsbereichs kann sich in Algebra und Analysis als sehr wichtig erweisen, da Sie damit beurteilen können, welche Werte von einer Funktion erreicht werden. Mit anderen Worten, Sie können den Satz aller Bilder über die Funktion finden
Die Aufgabe, herauszufinden, welche Punkte von einer Funktion erreicht werden können, ist sehr nützlich. Beispielsweise haben Sie möglicherweise eine Produktionsfunktion \(q(x)\), mit der Sie die für \(x\) Eingabeeinheiten erhaltene Ausgabemenge angeben können.
Wir möchten wissen, wie viele Eingabeeinheiten benötigt werden, um \(b\) Ausgabeeinheiten zu erzeugen. Mit anderen Worten, wir müssen \(x\) finden, damit \(q(x) = b\), eine andere Möglichkeit zu fragen, ob \(b\) im Bereich der Funktion \(q(x)\) liegt oder nicht.
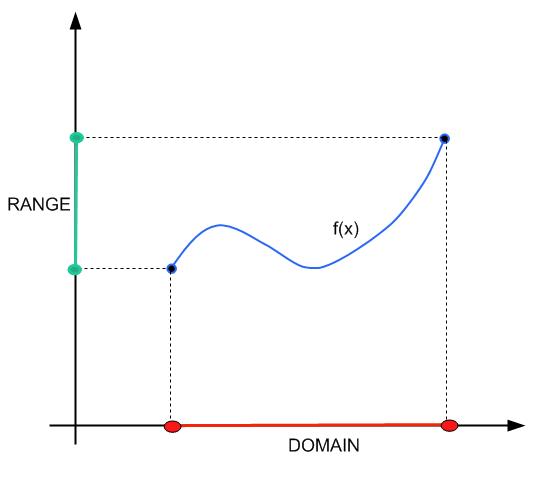
In diesem Tutorial konzentrieren wir uns mehr auf die Mechanik der Ermittlung des Bereichs. Für eine konzeptionellere Herangehensweise an Domäne und Reichweite können Sie Sehen Sie dieses Tutorial .
Der algebraische Weg, den Bereich einer Funktion zu finden
Genauso wie wir gelernt haben, wie man die Domäne berechnet, gibt es kein einziges Rezept, um den Bereich zu finden, es hängt wirklich von der Struktur der Funktion \(f(x)\) ab.
Es gibt jedoch eine algebraische Technik, die immer angewendet wird. Auf diese Weise finden Sie die Reichweite. Passt auf:
Angenommen, wir müssen den Bereich einer bestimmten Funktion \(f(x)\) ermitteln. Dann betrachten wir eine generische reelle Zahl \(y\) und versuchen, die folgende Gleichung für \(x\) zu lösen:
\[f(x) = y\]Wir müssen bestimmen, für welche Werte von \(y\) die obige Gleichung für \(x\) gelöst werden kann. Das ist es. Das kann natürlich schwierig sein, abhängig von der Struktur der Funktion \(f(x)\), aber es ist das, was Sie tun müssen.
Dies ist also der algebraische Weg, wie man den Bereich einer Funktion ohne grafische Darstellung findet.
BEISPIEL 1
Finden Sie den Bereich der Funktion \(\displaystyle f(x) = \frac{x+1}{x-3}\):
ANTWORTEN:
Wir gehen algebraisch vor: Sei \(y\) eine Zahl und lösen in der folgenden Gleichung nach \(x\): \(f(x) = y\). Der Wert \(y\) liegt im Bereich, wenn \(f(x) = y\) für \(x\) gelöst werden kann.
In diesem Fall haben wir:
\[\large f(x) = y \Leftrightarrow \frac{x+1}{x-3} = y\] \[\Rightarrow \,\,\,x+1 = y\left( x-3 \right)\] \[\Rightarrow \,\,\,x+1 = yx-3y\] \[\Rightarrow \,\,\,x-yx=-1-3y\] \[\Rightarrow \,\,\,x\left( 1-y \right)=-1-3y\] \[\Rightarrow \,\,\,x=\frac{3y+1}{y-1}\]Wann wird \(x\) gut definiert sein? Fast für alle \(y\), außer wenn \(y = 1\), weil wir in diesem Fall eine Division durch \(0\) haben. Daher ist der Bereich von \(f\) in diesem Fall die gesamte reelle Linie mit Ausnahme von 1.
Wenn wir die Intervallnotation verwenden, können wir \(Range(f) = (-\infty, 1) \cup (1, +\infty)\) schreiben.
BEISPIEL 2
Finden Sie den Bereich der Funktion \(f(x) = x^2 - 4x + 3\):
ANTWORTEN:
Wir gehen wieder algebraisch vor, damit Sie den Drill kennen: Sei \(y\) eine Zahl und wir lösen in der folgenden Gleichung nach \(x\): \(f(x) = y\). Der Wert \(y\) liegt im Bereich, wenn \(f(x) = y\) für \(x\) gelöst werden kann.
In diesem Fall haben wir:
\[\large f(x) = y \Leftrightarrow x^2 - 4x + 3 = y\] \[\Rightarrow \,\,\, x^2 - 4x + 3 - y = 0 \text{ (This is a quadratic equation in x)}\] \[\Rightarrow \displaystyle \,\,\, x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\] \[\Rightarrow \displaystyle \,\,\, x = \frac{-(-4) \pm \sqrt{(-4)^2 - 4(1)(3-y)}}{2(1)}\] \[\Rightarrow \displaystyle \,\,\, x = \frac{4 \pm \sqrt{16 - 4(3-y)}}{2}\] \[\Rightarrow \displaystyle \,\,\, x = \frac{4 \pm \sqrt{16 - 12 + 4y}}{2}\] \[\Rightarrow \displaystyle \,\,\, x = \frac{4 \pm \sqrt{4 + 4y}}{2}\] \[\Rightarrow \displaystyle \,\,\, x = 2 \pm \sqrt{1+y}\]Wenn Sie diesen endgültigen Ausdruck sehen, wann wird \(x\) gut definiert sein? Wir müssen haben, dass das Argument der Quadratwurzel nicht negativ sein muss, also brauchen wir:
\[1+y \ge 0\]was bedeutet, dass \(y \ge -1\). Wenn wir die Intervallnotation verwenden, können wir \(Range(f) = [-1, +\infty)\) schreiben.
In diesem Beispiel hätten wir es mit der Tatsache lösen können, dass \(f(x) = x^2 - 4x + 3\) eine quadratische Funktion ist und sein Graph eine Parabel ist, die sich nach oben öffnet.
Der minimale Punkt dieser Parabel wird am Scheitelpunkt erreicht. Die x-Koordinate des Scheitelpunkts ist:
\[\displaystyle x_V = \frac{-b}{2a} =\frac{-(-4)}{2(1)} =\frac{4}{2} = 2\]Die y-Koordinate des Scheitelpunkts wird nun einfach durch Einfügen des Werts \(x_V = 2\) in die quadratische Funktion ermittelt:
\[y_V = f(x_V) = 2^2 - 4(2) + 3 = -1\]Da der von der Parabel erreichte Mindestwert \(-1\) ist, schließen wir, dass der Bereich \([-1, +\infty)\) ist, was der gleichen Schlussfolgerung entspricht wie der algebraisch gefundene.
Das Diagramm der Funktion \(f(x) = x^2 - 4x + 3\) macht es noch deutlicher:
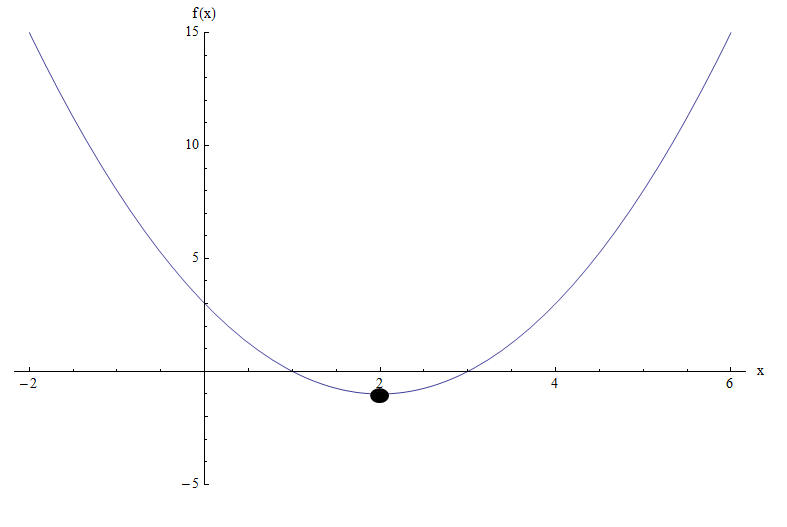
Wir können sehen, dass basierend auf dem Diagramm das Minimum bei \(x = 2\) erreicht wird, was genau das ist, was an der x-Koordinate des Scheitelpunkts gefunden wurde.
Das Risiko bei der Verwendung des Diagramms zum Ermitteln des Bereichs besteht darin, dass Sie möglicherweise die kritischen Punkte im Diagramm falsch interpretieren und eine ungenaue Bewertung der Stelle abgeben, an der die Funktion ihr Maximum oder Minimum erreicht.
Andere Strategien zum Ermitteln der Reichweite einer Funktion
Wie wir im vorherigen Beispiel gesehen haben, können wir manchmal den Bereich einer Funktion finden, indem wir nur ihren Graphen betrachten.
Angenommen, Sie möchten den Bereich der Funktion \(f(x) = x + 3\) ermitteln. Die Grafik ist unten dargestellt:
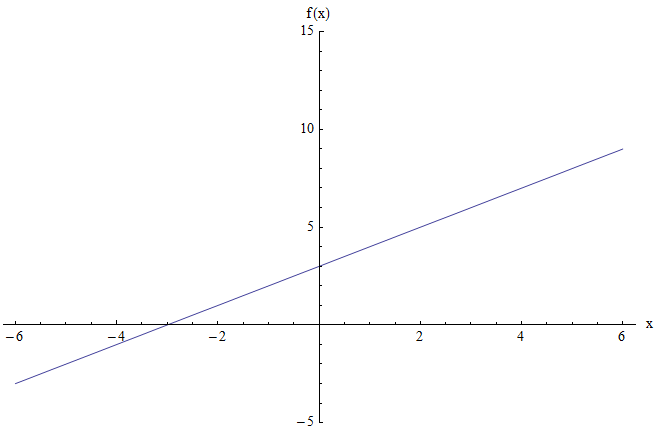
Die obige Grafik zeigt keine minimalen oder maximalen Punkte. Wenn \(x\) groß und positiv ist, ist der Wert der Funktion ebenfalls groß und positiv. Und analog ist, wenn \(x\) sehr negativ ist, der Wert der Funktion auch sehr negativ.
Die Intuition ist, dass die Funktion so negativ und so positiv sein kann, wie wir wollen, indem sie ausreichend große (positive oder negative) \(x\) -Werte auswählt. Und dann ist die Schlussfolgerung, dass der Bereich die gesamte reelle Linie ist, die \((-\infty, +\infty)\) unter Verwendung der Intervallnotation ist.
Eine solche Analyse ist in Bezug auf das Ergebnis korrekt, in Bezug auf die Argumentation jedoch schwach. Die "grafische Methode" zum Ermitteln des Bereichs hat dieses Problem: Sie ist aus intuitiver Sicht ansprechend, aber inhaltlich eher dünn.
Normalerweise sollten wir, wenn möglich, den analytischen / algebraischen Weg bevorzugen. Im Beispiel müssen wir nach \(x\) lösen:
\[x + 3 = y\] \[\Rightarrow \,\, x = y - 3\]Gibt es also eine Einschränkung für \(y\), damit \(x\) genau definiert ist? Überhaupt nicht, also gibt es keine Einschränkungen für \(y\) und die Schlussfolgerung ist, dass der Bereich die gesamte reale Linie ist.
Sie können diesen Artikel überprüfen, den Sie möchten wissen, wie man die Domäne einer Funktion findet stattdessen.
Es gibt viele gute algebraische Gründe, um den Bereich zu finden. Einer davon ist, dass er Teil der Prozesse für ist Finden der Umkehrung einer Funktion .
