Algebra Tutorials

So finden Sie die Umkehrung einer Funktion

Viele Anwendungen in Algebra und Analysis hängen davon ab, wie man die Umkehrung einer Funktion findet, und das ist das Thema dieses Tutorials.

Zunächst müssen Sie erkennen, dass Sie vor dem Auffinden der Umkehrung einer Funktion sicherstellen müssen, dass eine solche Umkehrung vorhanden ist.

Das Gute an der Methode zum Finden der Umkehrung, die wir verwenden werden, ist, dass wir die Umkehrung finden und herausfinden, ob sie gleichzeitig existiert oder nicht.

Bereit?? Dann schnall dich an.

Graph einer Funktion und ihrer Umkehrung

Wie können Sie feststellen, ob eine Funktion eine Inverse hat?

Technisch gesehen hat eine Funktion eine Umkehrung, wenn sie eins zu eins (injektiv) und surjektiv ist.

Die entscheidende Bedingung ist jedoch, dass es eins zu eins sein muss, da eine Funktion surjektiv gemacht werden kann, indem ihre Reichweite auf ihr eigenes Bild beschränkt wird.

Woher wissen Sie, wann eine Funktion eins zu eins ist?

Nun, es gibt zumindest ein paar Möglichkeiten. Einer ist der algebraische Weg und der andere der grafische Weg (ich wette, ich weiß, welchen Sie bevorzugen, oder?)

Algebraischer Weg

Damit eine Funktion \(f\) eins zu eins eins ist, müssen wir auf algebraische Weise beweisen, dass wir jedes Mal, wenn \(f(x) = f(y)\), diese \(x = y\) haben müssen.

Mit anderen Worten, wir müssen das beweisen

\[f(x) = f(y) \,\,\Rightarrow \,\, x = y\]

Grafischer Weg

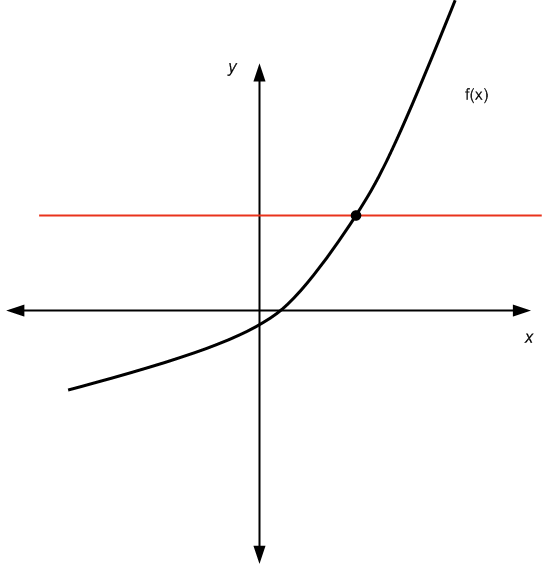
Für die grafische Darstellung müssen wir die verwenden horizontaler Linientest : Für jede horizontale Linie, die wir zeichnen, kreuzt der Graph der Funktion höchstens einmal diese horizontale Linie.

Grafisch:

Es besteht den horizontalen Linientest

Beispiel einer Funktion, die den horizontalen Linientest besteht

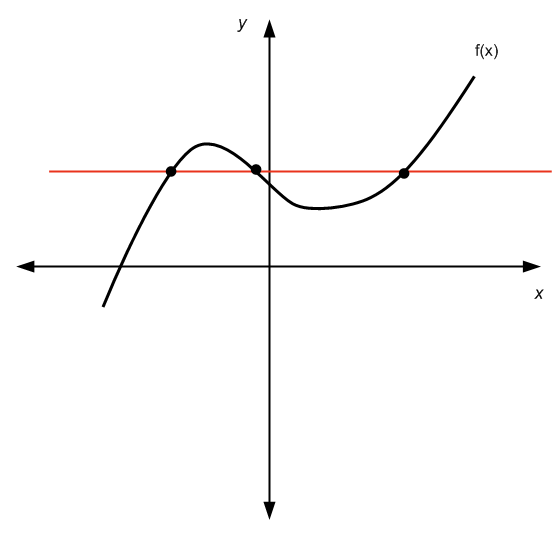
Der horizontale Linientest wird nicht bestanden

Beispiel für eine Funktion, die den horizontalen Linientest nicht besteht

Das Inverse finden

Um die Umkehrung einer gegebenen Funktion \(f(x)\) zu finden, müssen Sie eine Gleichung lösen.

In der Tat haben Sie die Gleichung \(f(x) = y\), Sie nehmen \(y\) als gegebene Zahl, und Sie müssen sie für \(x\) lösen, und Sie müssen sicherstellen, dass die Lösung EINZIGARTIG ist.

Das ist alles. Einfach richtig??

Nun zu den praktischen Schritten:

Schritt 1: Stellen Sie für ein gegebenes \(y\) die folgende Gleichung ein:

\[f(x) = y\]

und lösen Sie es für \(x\).

Schritt 2: Stellen Sie sicher, dass Sie darauf achten, für welche \(y\) es tatsächlich eine einzigartige Lösung gibt.

Schritt 3: Sobald Sie \(x\) in Bezug auf \(y\) lösen, ist dieser Ausdruck, der von \(y\) abhängt, Ihr \(f^{-1}(y)\).

Schritt 4: Ändern Sie den Variablennamen von \(y\) in \(x\) und Sie haben Ihre Umkehrfunktion \(f^{-1}(x)\).

BEISPIEL 1

Finden Sie die Umkehrung der Funktion \(f(x) = \sqrt x\)

ANTWORTEN:

Wir nehmen also \(y\) als gegeben und müssen \(f(x) = y\) lösen, was in diesem Fall dem Lösen entspricht

\[\sqrt x = y\]

Beachten Sie, dass die Quadratwurzel immer nicht negativ ist. Um eine Lösung zu finden, benötigen wir \(y\ge 0\).

Wenn wir auf beiden Seiten ein Quadrat anwenden, bekommen wir das

\[\Rightarrow \,\, (\sqrt x)^2 = y^2\] \[\Rightarrow \,\, x = y^2\]

Also, \(f^{-1}(y) = y^2\) und das Umschalten des Variablennamens, wir haben die Umkehrfunktion

\[f^{-1}(x) = x^2\]

für \(x\ge 0\).

BEISPIEL 2

Finden Sie die Umkehrung der Funktion \(f(x) = \displaystyle \frac{x}{x+1}\) für \(x > -1\)

ANTWORTEN:

Wieder nehmen wir \(y\) als gegeben, und jetzt müssen wir für \(x\) die Gleichung \(f(x) = y\) lösen. Also haben wir

\[\displaystyle \frac{x}{x+1} = y\] \[\Rightarrow \,\, x = y(x+1)\] \[\Rightarrow \,\, x = yx + y\] \[\Rightarrow \,\, x - yx = y\] \[\Rightarrow \,\, x(1 - y) = y\] \[\Rightarrow \displaystyle \,\, x = \frac{y}{1-y}\]

Also, \(f^{-1}(y) = \displaystyle \frac{y}{1-y}\) und das Umschalten des Variablennamens, wir haben die Umkehrfunktion

\[f^{-1}(x) = \displaystyle \frac{x}{1-x}\]

Weitere Informationen zum Finden der Umkehrung einer Funktion

Eine der entscheidenden Eigenschaften der Umkehrfunktion \(f^{-1}(x)\) ist \(f(f^{-1}(x)) = x\).

Denken Sie darüber nach, was dieses Ding sagt. So etwas wie: "Die auf der Umkehrung ausgewertete Funktion gibt Ihnen die Identität".

Mit anderen Worten, das Auswerten der Umkehrung durch die Funktion ist so, als würde man dem Argument nichts antun.

Oder wie manche Leute gerne sagen: Die Funktion kann das Inverse auf eine Art und Weise aufheben.

Sie wählen Ihre Version.

Wie finde ich die Umkehrung einer quadratischen Funktion? Können Sie?

Eigentlich lautet die Antwort: Es kommt darauf an. Dies liegt daran, wenn wir eine quadratische Funktion betrachten auf der ganzen realen Linie , dann ist es nicht 1-zu-1, da es den horizontalen Linientest nicht besteht, wie Sie in der folgenden Tabelle sehen können:

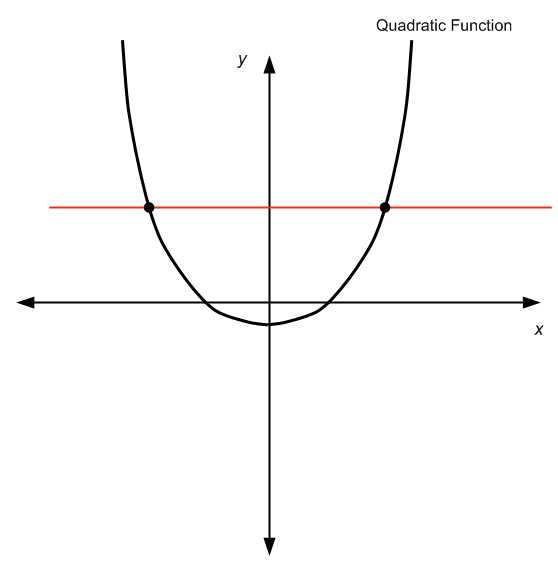
Quadratische Funktionen bestehen den horizontalen Linientest nicht

Wenn wir den Test der horizontalen Linie nicht bestehen, können wir sehen, dass es für einen gegebenen \(y\) mehr als einen \(x\) Wert gibt, so dass \(f(x) = y\), so dass wir nicht nach \(x\) "lösen" können, da es mehr als einen \(x\) gibt.

ABER, wenn Sie die Domain einschränken und nur die positiven Zahlen angeben, erhalten wir Folgendes:

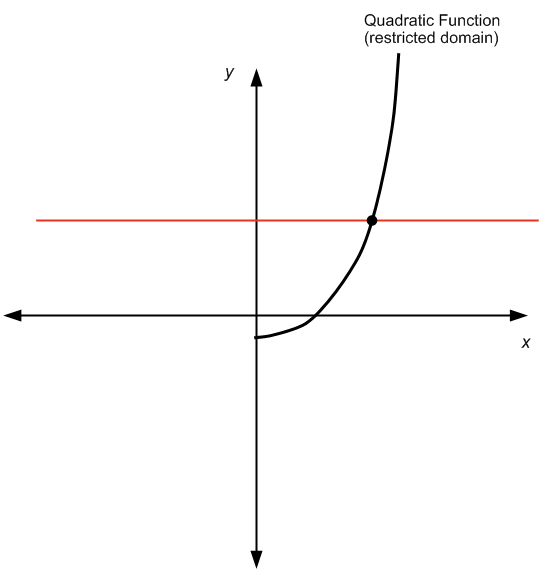
Quadratische Funktion in einer eingeschränkten Domäne

Dies besteht den Test der horizontalen Linie, und daher ist die quadratische Funktion invertierbar.

MORAL DER GESCHICHTE: Um zu überprüfen, ob etwas invertierbar ist, geht es NICHT nur um die Funktion. Es geht um die Funktion UND ihre Domäne und Reichweite .

So finden Sie schnell ein Diagramm für inverse Funktionen heraus

Es ist immer erforderlich zu beurteilen, ob die Funktion \(f(x)\) invertierbar ist oder nicht (indem geprüft wird, ob sie eins zu eins ist oder nicht). Unter der Annahme, dass Sie wissen, dass es invertierbar ist, gibt es eine einfache Möglichkeit, den Graphen der Inversen zu finden.

Stellen Sie zunächst die angegebene Funktion \(f(x)\) grafisch dar.

Zeichnen Sie dann die 45-Grad-Linie \(y = x\).

Um \(f^{-1}(x)\) grafisch darzustellen, müssen Sie lediglich das Diagramm von \(f(x)\) durch die 45-Grad-Linie \(y = x\) wie ein Spiegel spiegeln.

Siehe das folgende Beispiel mit den Funktionen \(f(x) = \sin x\) und \(f^{-1}(x) = \arcsin x\)