So finden Sie eine Domain
Das Erlernen des Auffindens der Domäne einer Funktion ist eine wichtige Fähigkeit in der Algebra, da Sie damit beurteilen können, wo eine Funktion richtig definiert ist. Oder mit anderen Worten, die Region, in der die Funktion ausgeführt werden darf
Die Aufgabe, herauszufinden, wo es gültig ist, eine Funktion zu bedienen, ist nützlich. Betrachten Sie beispielsweise die Funktion \(f(x) = \sqrt x\). Wir wissen, dass die Funktion Werte wie \(x \ge 0\) betreibt. Wir können nicht mit negativen Zahlen arbeiten, weil wir so etwas wie \(f(-1) = \sqrt{-1}\) bekommen würden, das nicht gut definiert ist (zumindest als reelle Zahl).
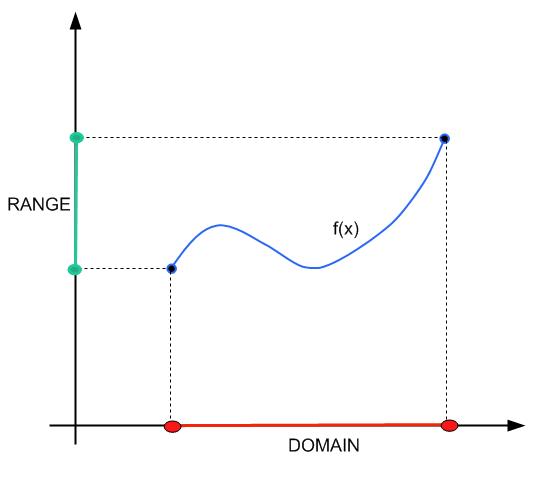
Sie können unser vorheriges Tutorial lesen, in dem wir ausführlich über das Thema gesprochen haben Domäne und Reichweite . Dieses Tutorial orientiert sich am operativen Teil der Suche nach der Domain.
Warum müssen wir die Domain finden?
Der Grund, warum wir die Domäne einer Funktion finden müssen, ist, dass jede Funktion einen bestimmten Satz von Werten hat, in denen sie definiert ist. Nicht alle Funktionen sind überall in der realen Linie definiert.
Die Domäne der Region in der realen Linie, in der sie sich befindet gültig mit der Funktion \(f(x)\) in Bezug auf die Werte arbeiten, die \(x\) annehmen kann.
Was müssen wir tun, um die Domain zu finden?
Wirklich, es gibt keinen Trick, der für alle Größen geeignet ist. Jede Funktion ist anders und es müssen je nach Funktion unterschiedliche Strategien verwendet werden, um die Domäne zu finden.
Es gibt zwei Techniken, die Sie IMMER berücksichtigen müssen:
Technik 1
: Stellen Sie sicher, dass es Divisionen durch Null gibt.
Darüber hinaus müssen diejenigen Punkte, die zu einer Division durch Null führen, aus der Domäne ausgeschlossen werden.
Technik 2
: Stellen Sie sicher, dass Divisions-Quadratwurzeln mit negativen Argumenten vorhanden sind (z. B. \(\sqrt{-1}\)).
Darüber hinaus müssen diejenigen Punkte, die zu einer Quadratwurzel einer negativen Zahl führen, aus der Domäne ausgeschlossen werden.
Letztendlich sollten Sie mit diesen beiden Techniken in der Lage sein, die Punkte auszusortieren, die nicht in der Domäne enthalten sind. Der Rest der Punkte in der realen Linie ist einfach Teil der Domäne.
Diese beiden Techniken lösen also das Problem, zu wissen, wie man die Domäne einer Funktion algebraisch findet. Eine andere Möglichkeit besteht darin, sich das Diagramm anzusehen, falls verfügbar.
BEISPIEL 1
Suchen Sie die Domäne der Funktion \(f(x) = \sqrt{x+4}+3\)
ANTWORTEN:
Das erste, was wir tun müssen und wo unser Erfolg beim Finden der Domäne liegt, ist zu bestimmen, wo wir möglicherweise ungültige Operationen finden können, wie z. B. Division durch Null oder negative Quadratwurzeln.
Für die Funktion \(f(x) = \sqrt{x+4}+3\) gibt es keine möglichen Teilungen durch Null, aber eine Quadratwurzel. Um ein gültiges Argument zu haben, darf das Argument innerhalb der Quadratwurzel nicht negativ sein.
Damit \(x\) in der Domäne der Funktion liegt, benötigen wir \(x\ge 0\). Dies impliziert, dass die Domäne von \(f\) \(\{x: x\ge 0\}\) oder \([0, +\infty)\) ist, wenn wir die Intervallnotation verwenden.
Ist das immer so einfach ?? Nicht wirklich, es kann so schwer werden, wie Sie es bekommen, abhängig von der Komplexität der Funktion \(f(x)\).
Normalerweise sind die Beispiele, die Sie in Ihren Tests und Hausaufgaben sehen, jedoch recht einfach. Lassen Sie uns in Bezug auf den Schwierigkeitsgrad eine Stufe höher schlagen.
BEISPIEL 2
Suchen Sie nun die Domäne der Funktion \(\displaystyle f(x) = \sqrt{\frac{x+4}{x-3}}\)
ANTWORTEN:
Diese Funktion ist etwas komplexer und erfordert eine sorgfältigere Behandlung. In diesem Fall müssen wir uns um mögliche Teilungen durch Null und negative Quadratwurzeln kümmern.
Erstens könnte es bei \(x = 3\) zu einer möglichen Division durch Null kommen, was darauf hinweist, dass \(x = 3\) aus der Domäne ausgeschlossen werden sollte.
Jetzt müssen wir uns um eine mögliche negative Quadratwurzel kümmern. Wir müssen das Vorzeichen von \(\displaystyle \frac{x+4}{x-3}\) bewerten. Außerdem muss es nicht negativ sein, also müssen wir lösen:
\[\displaystyle \frac{x+4}{x-3} \ge 0\]Damit eine Division nicht negativ ist, müssen entweder Zähler und Nenner positiv sein oder Zähler und Nenner müssen negativ sein.
Mit anderen Worten, wir brauchen sowohl \(x+4 \ge 0\) als auch \(x-3 > 0\) oder beide \(x+4 \le 0\) und \(x-3 < 0\).
Dies ist dasselbe wie \(x \ge -4\) und \(x > 3\) oder beide \(x \le -4\) und \(x < 3\).
Und dies kann als \(x > 3\) oder als beide \(x \le -4\) geschrieben werden, was dem Intervall \( (-\infty, -4] \cup (3, +\infty)\) entspricht.
Die Schlussfolgerung ist, dass die Domäne der Funktion \(\displaystyle f(x) = \sqrt{\frac{x+4}{x-3}}\) lautet:
\[ dom(f) = (-\infty, -4] \cup (3, +\infty)\]Wie Sie sehen, hat sich der Schwierigkeitsgrad etwas erhöht, und Sie können ihn tatsächlich so weit erhöhen, wie Sie möchten.
So finden Sie die Domäne einer rationalen Funktion
Lassen Sie uns zunächst daran erinnern, dass eine rationale Funktion der Quotient zweier Polynome der Form ist:
\[f(x) = \frac{p(x)}{q(x)} = \frac{a_0 + a_1 x + ...+ a_m x^m}{b_0 + b_1 x + ...+ b_n x^n}\]Wie finden Sie die Domäne für die oben genannte rationale Funktion? Wir müssen unserer Regel folgen: Suchen Sie nach möglichen Unterteilungen durch Null und negative Quadratwurzeln.
In diesem Fall gibt es keine potenziellen negativen Quadratwurzeln, aber es kann durch Null dividiert werden, wo immer das Polynom im Nenner Null ist.
Die Schlussfolgerung ist sehr einfach: Die Domäne einer rationalen Funktion ist die gesamte reelle Linie, AUSSER für die Punkte, an denen das Polynom im Nenner Null ist.
BEISPIEL 3
Finden Sie die Domain von
\[f(x) = \frac{x^2 + x + 1}{x^3 - 6x^2 + 11x - 6}\]ANTWORTEN:
Zunächst müssen wir verstehen, dass dies eine rationale Funktion ist, da Sie zwei Polynome \(p(x) = x^2 + x + 1\) und \(q(x) = x^3 - 6x^2 + 11x - 6\) im Zähler bzw. Nenner haben.
Der erste Schritt besteht also darin, die Nullen des Polynoms im Nenner zu finden. Wir müssen also Folgendes lösen: \[ x^3 - 6x^2 + 11x - 6 = 0\]
Diese Rechte ist das Gefühl, das schwer zu hören ist.
\[ x^3 - 6x^2 + 11x - 6 = (x-1)(x-2)(x-3) = 0\]was bedeutet, dass die Richtlinien des Polynoms im Nenner \(x_1 = 1, x_2 = 2, x_3 = 3\) sind. Die Kontakte ist, dass die Domäne der Funktion die gesamte reelle Linie ist, mit den Ausnahmen der Punkte 1, 2 und 3. Unter der Intervallnotation ist die Domäne \((-\infty, +\infty) \backslash \{1,2,3\}\).
Andere Strategien zum Finden der Domäne einer Funktion
Die Alternative, die Domäne einer Funktion zu finden, zu entschädigen Teilungen durch Null oder negativ Quadratwurzeln betrachtet werden, war die analytische Methode ist, besteht darin, den Graphen zu gehört.
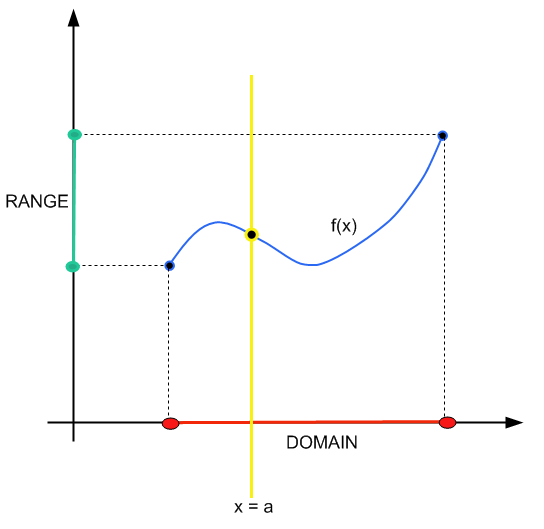
Die Methode ist einfach: Sie konstruieren eine Kontaktlinie \(x = a\). Wenn diese bestimmte Linie den Graphen der Funktion und eines Punktes kreuzt, gehört \(x = a\) zur Domäne.
Kurz und bündig.
Wie finden Sie die Möglichkeit, die Domäne einer Funktion mit einer Quadratwurzel?
Dies ist der Kern einer der Nachteile, über die wir gehört haben, führt negativ negativ Quadratwurzeln zu finden. Wenn Sie auch eine Funktion mit einer oder verschiedenen Quadratwurzeln haben, wissen Sie, dass es sehr wichtig ist, dass Sie eine negative Wurzel haben, und Sie haben sie erkannt.
Dies ist doch nicht immer der Herbst. Denken Sie an die Funktion \(f(x) = \sqrt{x^2}\). Diese Funktion hat eine Quadratwurzel, aber das Argument darin ist \(x^2\), war nicht negativ sein kann. Wir haben auch den Fall einer Funktion mit einem Quadratwurzel, die keine negativen Quadratwurzeln hat.