Das Erlernen des Faktorisierens ist eine der wichtigsten Fähigkeiten, die Sie erlernen können. Factoring hat so viele Anwendungen, dass Sie sich gerne die Zeit nehmen, alles darüber zu erfahren.

Eine kurze Auffrischung der kommutativen, assoziativen und verteilenden Eigenschaft. Für die reellen Zahlen \(x\), \(y\) und \(z\) haben wir die folgenden Eigenschaften

(Assoziativität der Addition) \((x+y)+z = x+(y+z)\)

Kommutativität der Addition) \( x + y = y + x\)

(Verteilungseigenschaft) \( x \cdot (y+z) = x \cdot y + x \cdot z\)

Dabei sind \(+\) und \(\cdot\) die Summe bzw. das Produkt reeller Zahlen.

Warum ist es nützlich zu wissen, wie man Faktoren berücksichtigt?

Es gibt viele Gründe, aber einer der entscheidenden ist, dass Factoring uns eine einfache Möglichkeit bietet, Gleichungen zu lösen. Factoring ist in der Tat DIE Art und Weise, wie wir Gleichungen lösen müssen.

Betrachten Sie zum Beispiel die Gleichung, in der wir versuchen, nach \(x\) zu lösen:

Wie gehen wir vor? Nun, wir können die Verteilungseigenschaft verwenden, um Folgendes zu erhalten:

Daher haben wir mit diesem letzten Ausdruck \( x(y+z) = 0\) ein Beispiel für Factoring. In der Tat haben wir den Anfangsausdruck \(xy+xz\) genommen und ihn in \( x(y+z)\) berücksichtigt.

Jetzt müssen wir eine einfachere Gleichung lösen, nämlich \( x(y+z) = 0\). Warum ist es einfacher? Weil wir jetzt wissen, dass das Produkt \( x(y+z)\) gleich Null ist, MUSS einer der Faktoren gleich Null sein.

Wenn wir also wissen, dass \(y+z = \not 0\), dann wissen wir, dass wir das \(x = 0\) haben müssen.

LEKTION : Ein Vorteil des Factorings besteht darin, dass eine Gleichung als Multiplikation von Faktoren gleich Null geschrieben werden kann. Dann muss mindestens einer der Faktoren Null sein.

Zum Beispiel, wenn wir nach \(x\) in der folgenden Gleichung lösen müssen:

Wir wissen nicht, dass wir tatsächlich faktorisieren, wenn wir das tun

Deshalb haben wir unsere Gleichung auf ein Produkt von Faktoren reduziert, das gleich Null ist: \(8x = 0\). Da einer der Faktoren \(8\) ungleich Null ist, ist die einzig mögliche Lösung \(x = 0\).

Mit anderen Worten : Wenn Sie wissen, wie man faktorisiert, werden Sie es wahrscheinlich wissen wie man Gleichungen löst .

Wie man Polynome berücksichtigt

Das Gleichgewicht wird mit einer sehr allgemeinen Klasse von Ausdrücken erreicht, die wir oftmals sehr systematisch berücksichtigen können. Diese Klasse ist die Klasse der Polynome. Zum Beispiel der Ausdruck

ist ein Polynom vom Grad 2. Oder der Ausdruck unten

ist ein Polynom vom Grad 3.

Im Allgemeinen ein Ausdruck der Form

ist ein Polynom vom Grad \(n\). Je einfacher der Ausdruck ist, desto einfacher wird es natürlich, ihn zu vereinfachen. Daher sollten wir zunächst lernen, wie man quadratische Ausdrücke faktorisiert. Dies sind Polynome zweiten Grades.

BEISPIEL 1

Berücksichtigen Sie den folgenden quadratischen Ausdruck

ANTWORTEN:

Dieses Beispiel zeigt Ihnen absichtlich, dass es schwierig sein kann, selbst den einfachsten Ausdruck wie den oben genannten zu berücksichtigen. Was würden Sie tun, um dies zu berücksichtigen?

Was ist, wenn ich Ihnen sage, dass Sie Null hinzufügen müssen? Es ist irgendwie lächerlich, oder? Mal sehn:

Stimmen Sie dem oben Gesagten zu? Ich habe gerade \(0\) hinzugefügt. Nichts hat sich verändert. Aber was ist, wenn ich dir das \(0 = 2x - 2x\) sage? Also dann

Alles das selbe! Es funktioniert, weil ich Null hinzugefügt habe, also ändert sich nichts. Aber jetzt erweitern wir es und gruppieren es:

Also endlich \(x^2 + x - 2 = (x+2)(x-1)\). Tricky? Vielleicht, aber das ist eine Möglichkeit, es zu tun. Obwohl dies ein kluger Weg ist, würden wir einen systematischeren Weg bevorzugen.

Faktor ein quadratisches Polynom

Clevere Tricks sind nett und das alles, aber normalerweise bevorzugen wir einen systematischen Ansatz, der niemals versagt. Für quadratische Polynome (Polynome vom Grad 2) gibt es eine systematische Vorgehensweise beim Factoring:

Schritt 1 : Mit dem quadratischen Ausdruck \(ax^2 + bx + c\) lösen wir zuerst die Gleichung

Schritt 2 : Wenn die Lösungen (Wurzeln) der obigen Gleichung real sind (auch wenn es nur eine Wurzel gibt), nennen wir diese Wurzeln \(x_1\) und \(x_2\). Mit diesen Wurzeln erhalten wir die folgenden Faktoren:

Die Lösungen \(x_1\) und \(x_2\) bestimmen also die Faktoren vollständig.

Natürlich ist in diesem Fall das Lösen einer quadratischen Gleichung erwartungsgemäß eng mit dem Faktorisieren der quadratischen Gleichung verbunden.

BEISPIEL 2

Berücksichtigen Sie die folgende quadratische Gleichung

durch die Berechnung seiner Wurzeln.

ANTWORTEN:

Wir beginnen mit der Lösung der entsprechenden quadratischen Gleichung:

mit dem berühmten und bekannten quadratische Formel ::

was bedeutet, dass die Lösungen (Wurzeln) \(x_1 = 1\) und \(x_2 = 1\) sind. Dann kann der quadratische Ausdruck \(x^2 - 4x + 3\) wie folgt berücksichtigt werden:

Beachten Sie, dass in diesem Fall der Term, der den Ausdruck \(x^2\) multipliziert, 1 ist, also in diesem Fall \(a = 1\).

Faktorisierung von Polynomen mit einem Grad größer als 2

Um quadratische Polynome zu faktorisieren, berechne ich einfach die Wurzeln der entsprechenden quadratischen Gleichung. Wie faktorisiere ich Polynome höheren Grades? Mit genau der gleichen Methode .

Schritt 1: Mit dem Polynomausdruck \(a_n x^n + a_{n-1}x^{n-1} + ... + a_1 x + a_0\) lösen wir zunächst die Gleichung

Schritt 2: Wenn die Lösungen (Wurzeln) der obigen Gleichung real sind (auch wenn sie wiederholt werden), nennen wir diese Wurzeln \(x_1\), \(x_2\), ..., \(x_n\). Mit diesen Wurzeln erhalten wir die folgenden Faktoren:

Es scheint also genauso einfach zu sein, ein Polynom vom Grad 2 zu faktorisieren wie ein Polynom vom Grad 10. Theoretisch lautet die Antwort ja.

Das einzige Problem ist, dass es keine einfache, enge algebraische Formel gibt, die Wurzeln für eine Polynomgleichung vom Grad 5 oder höher lösen kann.

Manchmal können wir Gleichungen höheren Grades lösen, indem wir uns die Grafik ansehen oder sogar den Taschenrechner verwenden. Überprüfen Sie beispielsweise die folgende Grafik:

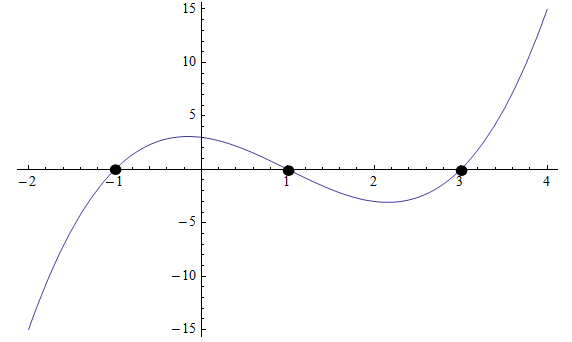
Grafisch können wir sehen, dass das Polynom die x-Achse an drei Punkten kreuzt: \(x_1 = -1\), \(x_2 = 1\) und \(x_3 = 3\), also sind dies die Wurzeln.

Wir wissen also, dass das Polynom die Form \(p(x) = a(x+1)(x-1)(x-3)\) haben muss. Wir müssten noch einen Punkt kennen, um die Konstante \(a\) zu kennen.