Logarithmische Gleichungen lösen
Das Lösen logarithmischer Gleichungen ist etwas, was Sie häufig tun müssen, wenn Sie sich mit algebraischen Verfahren befassen, und es lohnt sich, eine konkrete Strategie zu entwickeln, um mit ihnen umzugehen.
In diesem Tutorial lernen Sie die wichtigsten Strategien kennen, die Sie zur Lösung logarithmischer Gleichungen befolgen müssen.
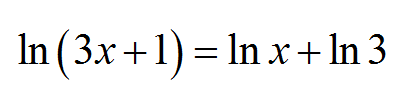
Was ist eine logarithmische Gleichung?
Als erstes müssen wir definieren, was eine logarithmische Gleichung ist.
Eine logarithmische Gleichung ist eine Gleichung, die mindestens eine unbekannte Variable umfasst, wobei ein logarithmischer Ausdruck auf mindestens einer Seite der Gleichung erscheint
.
Ein Beispiel für eine logarithmische Gleichung ist
\[\ln x = 2\ln x - \ln 3\]oder auch
\[ \ln(3x-1) - \ln(2x + 1) = 1\]
Beachten Sie, dass eine logarithmische Gleichung mehr als eine unbekannte enthalten kann, wie zum Beispiel
Strategien zur Lösung logarithmischer Gleichungen
Der erste Haftungsausschluss ist, dass es weder kugelsichere Möglichkeiten zum Lösen einer logarithmischen Gleichung noch eine allgemeine Gleichung gibt. Der Grund dafür ist, dass alle Methoden eine bestimmte Struktur in der Gleichung annehmen, die nicht unbedingt in allen Gleichungen vorhanden ist.
Wir können also NICHT DEN Weg finden, logarithmische Gleichungen zu lösen, weil es keinen Weg gibt, der alle möglichen Fälle behandelt.
Es gibt jedoch einige Strategien, die Ihnen die beste Chance geben, die Gleichung durchzugehen und eine Lösung zu finden, falls es eine gibt.
Versuchen Sie zunächst, alle logarithmischen Ausdrücke in einem logarithmischen Ausdruck zu gruppieren.
Dies wird typischerweise durch Verwendung der gebräuchlichsten erreicht Protokollregeln , mit denen Sie einen logarithmischen Ausdruck komprimieren können, wenn die Struktur des Ausdrucks dies zulässt.
Zweitens, sobald die logarithmischen Ausdrücke so weit wie möglich komprimiert sind, werden Sie sie entfernen, indem Sie normalerweise die Exponentialfunktion auf beide Seiten der Gleichheit anwenden.
Dieser letzte Schritt entfernt hoffentlich alle Logarithmen aus dem Bild und ermöglicht es Ihnen, nach Unbekannten zu suchen.
Mit anderen Worten, das Lösen einer logarithmischen Gleichung besteht darin, die logarithmischen Ausdrücke zu gruppieren, sie durch Anwenden von Exponentialausdrücken zu eliminieren und die Gleichung dann als reguläre Gleichung zu lösen.
Wenn Sie die Logarithmen losgeworden sind, stehen Sie natürlich vor einer Gleichung, die ihre eigenen Herausforderungen haben könnte.
Lösen verschiedener Beispiele für logarithmische Gleichungen
Es gibt keinen besseren Weg, um zu lernen, wie man Gleichungen löst, als sie tatsächlich zu lösen:
BEISPIEL 1:
Löse die folgende Gleichung:
\[\large 4 \log(\sqrt x) = \log(6x-1)\]ANTWORTEN:
Folgen wir den Strategien. Die Idee ist, die logarithmischen Ausdrücke so weit wie möglich zu komprimieren. Dies ist ein Urteilsspruch, da die Hauptidee darin besteht, die Logarithmen im Wesentlichen loszuwerden.
Mit den Protokollregeln können wir die "4" innerhalb des Logarithmus als setzen
\[\large 4 \log(\sqrt x) = \log(6x-1)\] \[\large \Rightarrow \log((\sqrt x)^4) = \log(6x-1)\] \[\large \Rightarrow \log(x^2) = \log(6x-1)\]Jetzt, da die logarithmischen Ausdrücke so komprimiert wie möglich sind, müssen wir die Logarithmen entfernen.
Eine Möglichkeit besteht darin, die Exponentialfunktion \(10^x\) auf jede Seite der Gleichheit anzuwenden. Was meine ich damit ???
Nun, Sie haben zwei Seiten in dieser Gleichheit. Da beide Seiten gleich sind, sollte bei Verwendung als Argumente der Funktion \(10^x\) die Gleichheit erhalten bleiben. Also haben wir
\[\large \log(x^2) = \log(6x-1)\] \[\large \Rightarrow 10^{\log(x^2)} = 10^{\log(6x-1)}\] \[\large \Rightarrow x^2 = 6x-1\]weil wir wissen, dass \(10^{\log a} = a\), eine der grundlegenden Protokollregeln.
Nachdem wir die Logarithmen eliminiert haben, können wir die verbleibende Gleichung lösen:
\[\large x^2 = 6x-1\] \[\large \Rightarrow x^2 - 6x + 1 = 0\] \[\large \Rightarrow x = \frac{-(-6) \pm \sqrt{(-6)^2-4(1)(1)}}{2(1)}\] \[\large \Rightarrow x = \frac{6 \pm \sqrt{36-4}}{2}\] \[\large \Rightarrow x = \frac{6 \pm \sqrt{32}}{2}\] \[\large \Rightarrow x = \frac{6 \pm 4\sqrt{2}}{2}\] \[\large \Rightarrow x = 3 \pm 2\sqrt 2\]also dann \(x_1 = 3 + 2\sqrt 2\) und \(x_2 = 3 - 2\sqrt 2\). Technisch müssen Sie überprüfen, ob diese beiden Lösungen der ursprünglichen Gleichung sind, um sicherzustellen, dass sie zur Domäne der logarithmischen Ausdrücke gehören.
In diesem Fall sind sowohl \(x_1 = 3 + 2\sqrt 2\) als auch \(x_2 = 3 - 2\sqrt 2\) die Lösungen der ursprünglichen Gleichung.
BEISPIEL 2:
Lösen Sie die folgende logarithmische Gleichung:
\[\large \ln 5 - \ln(6-x) = \ln x\]ANTWORTEN:
Mit den Protokollregeln können wir die Protokollausdrücke komprimieren, das bekommen wir
\[\large \ln 5 - \ln(6-x) = \ln x\] \[\large \displaystyle \Rightarrow \ln\left(\frac{5}{6-x}\right) = \ln x\] \[\large \displaystyle \Rightarrow e^{\ln\left(\frac{5}{6-x}\right)} = e^{\ln x}\] \[\large \displaystyle \Rightarrow \frac{5}{6-x} = x\]weil wir wissen, dass \(e^{\ln a} = a\), eine der grundlegenden Protokollregeln.
Nachdem wir die Logarithmen eliminiert haben, können wir die verbleibende Gleichung lösen:
\[\large \displaystyle \frac{5}{6-x} = x\] \[\large \displaystyle \Rightarrow 5 = x(6-x)\] \[\large \displaystyle \Rightarrow 5 = 6x - x^2\] \[\large \displaystyle \Rightarrow x^2 -6x + 5 = 0\] \[\large \displaystyle \Rightarrow (x-1)(x-5) = 0\]also dann \(x_1 = 1\) und \(x_2 = 5\). Lassen Sie uns diese Werte in die ursprüngliche Gleichung einfügen, um zu sehen, ob es sich tatsächlich um Lösungen handelt:
Für \(x_1 = 1\):
Das ist das gleiche wie:
\[\large \ln 5 - \ln(5) = 0\]Das ist wahr, so gilt die Gleichung.
Für \(x_1 = 5\):
Das ist das gleiche wie:
\[\large \ln 5 - \ln(1) = \ln(5)\]Das ist wahr, so gilt die Gleichung.
Daher sind die Lösungen für die Gleichung \(x_1 = 1\) und \(x_2 = 5\).
Weitere Informationen zum Lösen logarithmischer Gleichungen
Eine Sache, über die sich die Schüler am meisten Sorgen machen, ist, wie Sie das Log in einer Gleichung loswerden können. Aber wir haben gesehen, dass das eigentlich der einfache Teil ist. Schwieriger ist es, den Ausdruck tatsächlich algebraisch zu bearbeiten, damit die Protokolle entfernt werden können.
Das wirft die Frage auf, wie mit verschiedenen Grundlagen umgegangen werden soll, was einen eigenen Absatz erfordert.
Lösen logarithmischer Gleichungen mit unterschiedlichen Grundlagen
In den obigen Beispielen haben wir uns nur mit \(\log\) (Logarithmus mit Basis 10) und \(\ln\) (Logarithmus mit Basis \(e\)) befasst. Wie machst du das, wenn du einen Logarithmus mit einer anderen Basis hast, wie \(\log_a\) ???
Die Antwort ist einfach: Um Logarithmen mit einer anderen Basis zu eliminieren, sagen wir \(\log_a\) mit der Basis \(a\), verwenden wir einfach die Exponentialfunktion \(a^x\). Einfach richtig?
In der Tat ist das Eliminieren des Logarithmus der einfache Teil des Lösens von Log-Gleichungen. Der schwierigere Teil des Prozesses besteht darin, die logarithmischen Ausdrücke in einer Form zu gruppieren und zu komprimieren, in der Sie sie entfernen.
Weitere Informationen zur Funktionsweise der logarithmischen Funktion finden Sie unter Sehen die Eigenschaften Waden Graphen und studieren die Grundlegende Protokollregeln .