Algebra Tutorials

Suchen des Protokolldiagramms

Die Methode zum Auffinden des Protokolldiagramms ist allen logarithmischen Funktionen gemeinsam. Dies liegt daran, dass alle logarithmischen Funktionen zumindest strukturell im Wesentlichen die gleiche Form haben, sondern nur von der Basis des Logarithmus abhängen.

Erinnern wir uns zunächst an die logarithmische Funktion mit der Basis \(a\), \(\log_a x\). Die am häufigsten verwendeten Basen sind \(a = 10\). In diesem Fall schreiben wir einfach \(\log x\) und in diesem Fall \(a = e\). In diesem Fall schreiben wir \(\ln x\) und nennen es das natürliche Protokoll.

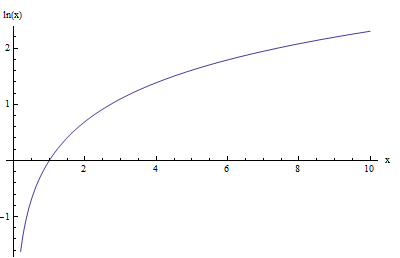
Das Diagramm der natürlichen Protokollfunktion \(\ln x\) ist beispielsweise unten dargestellt:

Lassen Sie uns nun sehen, was passiert, wenn wir \(\log x\) und \(\ln x\) grafisch darstellen (dies ist die Protokollbasis 10 und das natürliche Protokoll):

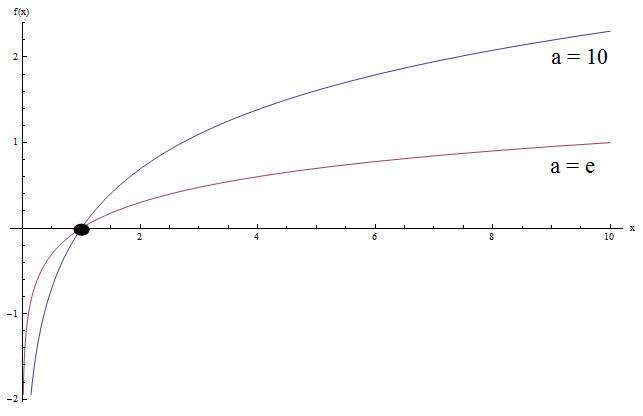
Natürliches Protokoll und Protokollbasis 10

Sehen Sie Ähnlichkeiten? Nun, es gibt einige.

Beachten Sie, dass beide Diagramme dieselbe allgemeine konkave Form haben. Außerdem kreuzen beide Graphen die y-Achse bei \(x = 1\) (was keine Überraschung ist, da \(\log_a 1 = 0\) für alle Basen mit \(a > 0\) gilt).

Eine andere Sache ist, dass sich beide Graphen der negativen Unendlichkeit nähern, wenn sich \(x\) 0 nähert, und der Unendlichkeit, wenn sich \(x\) der Unendlichkeit nähert.

Was ist, wenn wir versuchen, logarithmische Funktionen mit \(0 < a < 1\) grafisch darzustellen? Überprüfen Sie das folgende Beispiel:

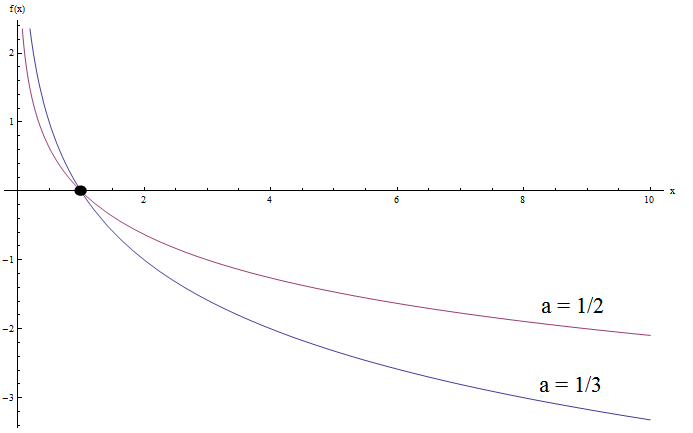
Protokollfunktionen mit einer Basis von weniger als 1

Sehen Sie jetzt Ähnlichkeiten? Natürlich.

Beachten Sie, dass beide Diagramme dieselbe allgemeine konvexe Form haben. Außerdem kreuzen beide Graphen erneut die y-Achse bei \(x = 1\), was erwartet wird.

Jetzt nähern sich beide Graphen der Unendlichkeit, wenn sich \(x\) 0 nähert, und der negativen Unendlichkeit, wenn sich \(x\) der Unendlichkeit nähert. Es ist eine Art entgegengesetztes Verhalten, wenn die Basis \(a\) größer als 1 ist.

Wie erstellen Sie ein Protokolldiagramm?

Basierend auf dem, was wir in den vorherigen Beispielen gefunden haben, können wir einige Regeln einfügen, die Sie verwenden können, wenn Sie Protokolldiagramme erstellen möchten:

Angenommen, Sie möchten die Funktion \(y = \log_a x\) für \(a > 0\) grafisch darstellen. Dann:

Schritt 1 : IMMER kreuzt die logarithmische Funktion die y-Achse bei \(x = 1\).

Schritt 2 : Wenn \(a > 1\), wird das Diagramm vergrößert und konkav. Ebenfalls:

\[\lim_{x\to 0^+} \log_a x = -\infty, \,\, \lim_{x\to \infty} \log_a x = \infty\]

Schritt 3 : Wenn \(0 < a < 1\), dann nimmt der Graph ab und ist konvex. Ebenfalls:

\[\lim_{x\to 0^+} \log_a x = \infty, \,\, \lim_{x\to \infty} \log_a x = -\infty\]

Einfach richtig??

Weitere Informationen zu Protokolldiagrammen

Zuallererst ist es eine entscheidende Fähigkeit, zu wissen, wie man eine Funktion grafisch darstellt der Graph einer Funktion gibt Ihnen eine Menge Informationen darüber.

In den vorherigen Abschnitten haben wir erfahren, wie sich die Basis eines Protokolls auf das Diagramm auswirkt. Das Interessante ist, dass die Form und das Verhalten des logarithmischen Graphen nur davon abhängen, ob \(a > 1\) und \(0 < a < 1\).

Kann ein Protokoll einer negativen Zahl entsprechen?

Nun, wir müssen spezifizieren, was wir damit meinen. Erstens kann die Basis der logarithmischen Funktion nicht negativ sein. Auch das Argument einer logarithmischen Funktion kann nicht negativ sein.

ABER der Logarithmus einer Zahl kann absolut negativ sein. Zum Beispiel: \(\ln(1/e) = -1\).

Wie stellen Sie inverse Protokollfunktionen grafisch dar?

Nun, das erste, was Sie wissen müssen, ist, dass die Umkehrung einer Protokollfunktion immer eine Exponentialfunktion ist.

Die grafische Darstellung der Umkehrung einer Protokollfunktion ist also so einfach wie das Erkennen der entsprechenden Exponentialfunktion und die grafische Darstellung.

Es gibt auch andere Methoden. Sie können das ursprüngliche Protokolldiagramm zeichnen und ein Diagramm zeichnen, das in Bezug auf das 45 symmetrisch zu diesem angegebenen Protokolldiagramm ist ^Ö gerade Linie \(y = x\).

Oder verwenden Sie das Originaldiagramm und ändern Sie den Wert von \(x\) um den Wert von \(y\).

Dieses Tutorial orientiert sich an den grafischen Eigenschaften der logarithmischen Funktion. Für die Definition und Führer Protokollregeln, Rechte Sie diese .