Der Graph einer Funktion ist eine Menge geordneter Paare \((x,y)\). Oder der Graph einer Funktion ist eine Konzeptualisierung, bei der wir eine Reihe von Paaren \((x,y)\) auf einem Koordinatensystem ausführen. Ich sage, es ist eine Konzeptualisierung, weil die Art und Weise, wie wir einen Graphen darstellen, bis zu einem gewissen Grad eine optische Täuschung ist.

Warum sage ich das? Schauen Sie doch mal rein. Woran denkst du, wenn ich "Graph" sage? Überprüfen Sie die Abbildung vor.

Das ist also eine Grafik. Eine Reihe von \((x, y)\) Paaren oder wie wir sie auch nennen können, Punkte. Ein bestimmter Punkt wird unten hervorgehoben

Der Trick oder die visuelle Illusion ist, dass ein Punkt theoretisch keine Dimensionen hat (keine Breite, keine Länge). Diese "Kurve", die wir zeichnen, um einen Graphen darzustellen, ist eine bequeme Art, einen Graphen darzustellen, aber wir betrügen, weil diese Darstellung eine Kurve hat, die eine Dicke hat.

Das soll also nicht auf Ihrer Parade regnen, sondern nur klarstellen, dass das, was Sie als Grafik verstehen, eher eine ist Darstellung eines Diagramms, das bequem und glaubwürdig ist.

Mit Funktionen verknüpfte Diagramme

Eine wirklich einfache Möglichkeit, ein Diagramm zu definieren, ist die Verwendung einer Funktion \(f(x)\). In der Tat ist ein durch eine Funktion \(f(x)\) definierter Graph die Menge aller Punkte \((x, f(x))\) für \(x \in D\), wobei \(D\) die Domäne der Funktion \(f\) ist.

Die Darstellung ist die gleiche wie in den vorherigen Diagrammen, nur dass wir jetzt Folgendes tun:

In diesem Fall besteht der deutlichste Unterschied darin, dass die zweite Komponente des Paares \((x,y)\) nicht irgendein Wert \(y\) ist. Die zweite Komponente ist \(f(x)\), daher wird sie eindeutig von \(x\) bestimmt.

BEISPIEL 1

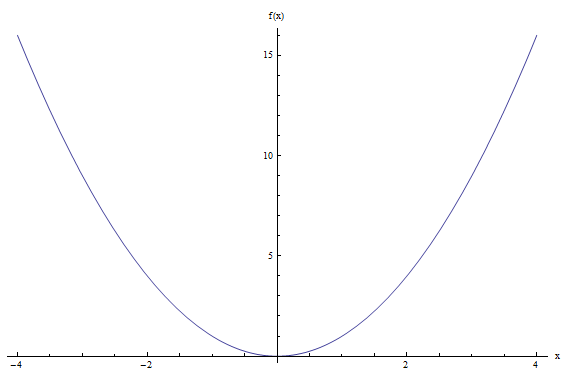
Zeichnen Sie den Graphen der Funktion \(f(x) = x^2\).

ANTWORTEN:

Nichts Seltsames, wir müssen nur den Graphen einer Funktion ändern. Die Punkte in der Grafik haben die Form \((x, f(x)) = (x, x^2)\). Dies bedeutet, dass der Wert von \(x\) \(x^2\) im Diagramm wird ist.

Beispiele für Punkte in der Grafik: \((1, 1)\), \((2, 2^2) = (2, 4)\), \((3, 3^2) = (3, 9)\) usw. Grafisch erhalten wir die gleichen Darstellung der Grafik:

Kontinuierliche versus diskontinuierliche Graphen

Eine der Bedenken, die wir in unseren Köpfen treffen, wenn wir ein Diagramm denken, ist, dass es glatt und ohne Sprächen ist. Das ist nicht immer der Herbst. Es gibt Funktionen, die zu Funktionen gehören, die springen oder sogar zu Graphen führen. Andere Funktionen haben Diagramme, die sehr glatt sind, wie es bei \(f(x) = x^2\) besteht ist.

Das Konzept der Glätte einer Funktion wird im Kalkül formal mit dem Begriff der rechtlichen Funktionen Funktion. Aber ohne viel Flaum können wir sagen, dass wir vorerst denken werden, dass eine stetige Funktion eine Funktion ist, die einen "glatten" Graphenhut und eine diskontinuierliche Funktion ist eine Funktion, die nicht glatt ist oder "Spricht" hat.

BEISPIEL 2

Ist die Funktion \(f(x) = sin(x)\) stetig?

ANTWORTEN:

Nun, wir sterben wieder eine formale Kontinuitätsanalyse, um zu ändern. Lassen Sie uns uns uns der obersten informellen Definition die Grafik bezieht. Der Computer gibt uns welche:

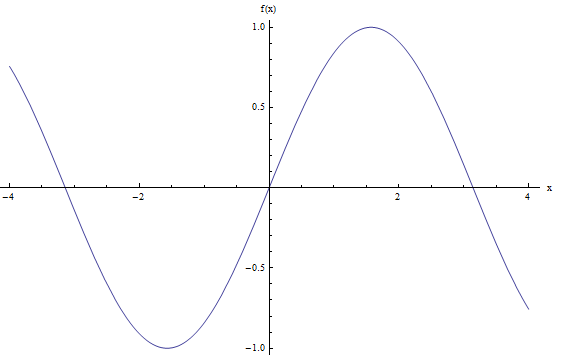
Ich würde sagen, dass die obige Grafik ohne Sprächen sehr glatt funktioniert. Wenn wir auch unsere naive Definition haben, sagen ich sagen, dass \(f(x) = \sin x\) stetig ist.

BEISPIEL 3

Ist die Funktion \( f\left( x \right)=\left\{ \begin{array}{cc}-1 &\,\,\,\,\text{for } x\le 1 \\ \\ x & \,\,\,\,\,\,\text{for }x>1 \\ \end{array} \right.\) stetig?

ANTWORTEN:

Um die Frage zu ändern, müssen wir das Diagramm ändern. Der Computer gibt uns welche:

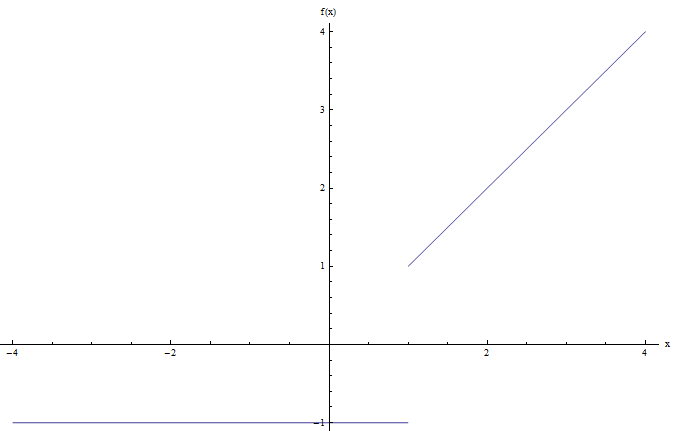
Dies Sie, dass es am Punkt ist \(x = 1\) einen Sprung gibt, wohalten ich sagen, dass der obige Graph einen Sprung hat, und wo ist diese Funktion diskontinuierlich.

Weitere Informationen zu gehört

Die Verwendung von Diagrammen zur Darstellung einer Funktion kann eine Rolle Rolle für das Verhalten des Verhaltens einer Funktion spielen.

Es gibt sich um analytische (Kalkül-) Werkzeuge, um das Verhalten einer Funktion \(f(x)\) zu verstehen, ohne dass sie zu gehört. Es ist nur sehr wichtig, ein Diagramm zu sehen, da es eine sehr schnelle Position ist, sich ein Bild von der Funktionsweise der Funktion zu machen.

Dies Sie, dass nicht alle Diagramme von Funktionen sind sind. Erkennen kann Diagramme auch aus Beziehungen beziehen. Sehen Sie sich die Grafik unter und sagen Sie mir, ob Sie können können, welche Beziehung damit verbunden ist.

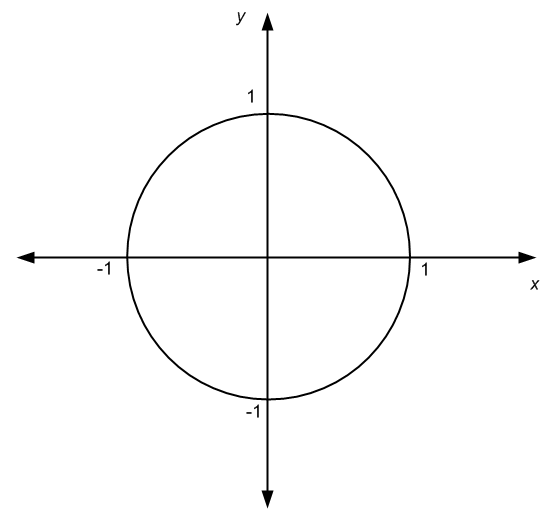
Sie haben es richtig gemacht, dass der obige Graph die Darstellung der Einheit einer Einheitskreises \(x^2 + y^2 = 1\) ist, die, wie wir bereits wissen, eine Beziehung und keine Funktion bestimmt.

Wenn Sie ein Diagramm erstellen müssen, müssen Sie es aus Funktionsgraphen um eine gute Darstellung des Verhaltens der Funktion zu erhalten.