Mehr zu diesem Determinantenrechner.

In linearen Algebra und in der Verwendung von Matrizen ist die Idee der Determinante einer Matrix \(A\) ein Konzept von der tiefsten Bedeutung.

Dies liegt daran, dass seine Verwendung mit fast jeder bedeutenden Operation verbunden ist, die Sie mit Matrizen, wie z. B. Überprüfung der Invertierbarkeit von Matrizen, tun möchten, Fundkenmatrix der Umkehrung Einer oder Lösungssystem .

Wo immer Sie sich bei der Arbeit mit Matrizen umsehen, finden Sie Determinanten auf die eine oder andere Weise.Es ist also sehr wichtig, sich mit ihnen vertraut zu machen.

Wie kann Ihnen dieser Matrixrechner helfen?

1. Sie müssen lediglich Ihre Matrix eingeben
2. Es muss eine quadratische Matrix sein, dies ist eine Matrix mit der gleichen Anzahl von Zeilen und Spalten
3. Klicken Sie einfach auf die Schaltfläche und der Taschenrechner zeigt Ihnen alle Schritte und den Endwert der Determinante an
4. Die Arbeit an Determinantenberechnungen kann äußerst mühsam und anfällig für Fehler sein.Dieser Taschenrechner erspart Sie vor diesen Problemen

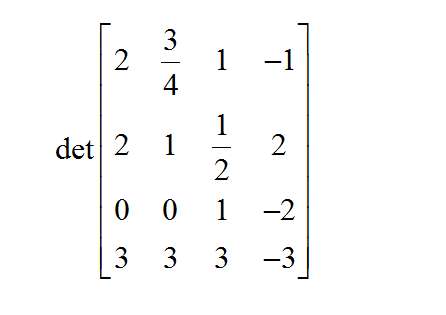
Wie berechnet man die Determinante einer Matrix?

Das könnte eine lange Antwort sein, da es viele Möglichkeiten gibt, die Determinante einer Matrix zu berechnen.Lassen Sie uns zunächst sagen, dass die Determinante nur für quadratische Matrizen berechnet werden (dies sind Matrizen, die die gleiche Anzahl von Zeilen und Spalten haben).

Die kleinste Matrix, für die wir eine Determinante berechnen können, ist eine 2x2 -Matrix.Betrachten wir eine generische 2x2 -Matrix, wie unten gezeigt:

\[ A = \begin{bmatrix} a & b \\ c & d \end{bmatrix}\]

Was ist die Formel der Determinante?In diesem Fall wird die Determinante der Matrix \(A\) einfach als \(\det(A) = a d - bc\) berechnet

Also zum Beispiel, wenn wir:

\[ A = \begin{bmatrix} 1 & 2 \\ 1 & 3 \end{bmatrix}\]

Die Determinante der Matrix \(A\) wäre \(\det(A) = 1 \cdot 3 - 2 \cdot 1 = 3 - 2 = 1\).Einfach richtig?

Wie finden Sie die Determinante einer 3x3 -Matrix?

Für größere Matrizen bauen wir nun die Berechnung der Determinanten basierend auf der Unterdeterminante kleinere Matrizen auf.Um Ihnen einen Geschmack zu geben, sehen wir uns eine Möglichkeit, die Determinante einer 3x3 -Matrix zu berechnen.In Betracht ziehen

\[ A = \begin{bmatrix} a & b & c \\ d & e & f \\ g & h & i \end{bmatrix}\]

In diesem Fall wird die Determinante der Matrix 3x3 -Matrix \(A\) basierend auf dem Betrieb mehrerer 2x2 -Determinanten berechnet

\[\det(A) = a \det \begin{bmatrix}e & f \\ h & i \end{bmatrix} - b \det \begin{bmatrix} d & f \\ g & i \end{bmatrix} + c \det\begin{bmatrix} d & e \\ g & h \end{bmatrix}\]

In den obigen Gleichungen spielt die Werte \(a\), \(b\), \(c\) die Rolle von Pivots, und das kann ein negatives Vorzeichen erhalten.Das Zeichen eines Drehes ist \((-1)^{i+j}\), wobei der entsprechende Drehpunkt in Zeile \(i\) und Spalte \(j\) ist.

Zum Beispiel \(a\) ist in Zeile 1, Spalte 1, also ist sein Vorzeichen \((-1)^{1+1} = (-1)^2 = 1\) (positiv).Außerdem ist \(b\) in Zeile 1, Spalte 2, also ist sein Vorzeichen \((-1)^{1+2} = (-1)^3 = -1\) (negativ) und so weiter.

Die Magie besteht darin, eine Zeile oder Spalte als Pivots zu wählen.Jeder Drehzahl hat ein Vorzeichen (positiv oder negativ) und ein Unterabwert, das mit dem zusammenhängt Matrix -cofaktoren .

Dieses Unterdeterminant ist die tatsächliche Determinante der ursprünglichen Matrix nach dem Entfernen von Zeile \(i\) und Spalte \(j\) für Pivot, die in einer Reihe \(i\) und Spalte \(j\) ist.

Die logischste Konvention zeigt an, die Zeile oder Spalte mit den meisten Nullen für die Pivots auszuwählen.

Wie finden Sie die Determinante einer 3x4 -Matrix?

Du kannst das nicht machen.Eine 3x4 -Matrix ist keine quadratische Matrix, und daher kann keine Determinante berechnet werden.Um eine Determinante zu berechnen, muss die Matrix die gleiche Anzahl von Zeilen und Spalten haben.

Ein 4x4 -Determinant -Rechner

Für größere Matrizen ist die Methodik gleich: Wählen Sie eine Zeile oder Spalte für Pivots, idealerweise mit den meisten Nullen.Das Finden des Zeichens, das jedem Drehzahl entspricht, und die entsprechenden Unterdeterminanten.

Daher reduzieren Sie die Berechnung der Determinanten einer 4x4 -Matrix in den Betrieb von vier 3x3 -Determinanten.Und wiederum wird jeder der 3x3 -Determinanten als Betrieb mehrerer 2x2 -Determinanten gefunden, für die wir eine Formel kennen.

Es kann also sehr schnell chaotisch werden.

Beispiel für die Berechnung einer Matrixdeterminante

Frage: Betrachten Sie die folgende Matrix:

\[ \begin{bmatrix}1&2&3\\3&1&4\\2&3&8\end{bmatrix}\]

Berechnen Sie die Determinante der angegebenen Matrix und zeigen Sie die Schritte an.

Lösung: Wir müssen die Determinante der angegebenen \(3 \times 3\) Matrix berechnen.

Verwenden der subdeterminanten Formel, die wir erhalten:

\[ \begin{vmatrix} \displaystyle 1&\displaystyle 2&\displaystyle 3\\[0.6em]\displaystyle 3&\displaystyle 1&\displaystyle 4\\[0.6em]\displaystyle 2&\displaystyle 3&\displaystyle 8 \end{vmatrix} = 1 \cdot \left( 1 \cdot \left( 8 \right) - 3 \cdot \left(4 \right) \right) - 2 \cdot \left( 3 \cdot \left( 8 \right) - 2 \cdot \left(4 \right) \right) + 3 \cdot \left( 3 \cdot \left( 3 \right) - 2 \cdot \left(1 \right) \right)\] \[ = 1 \cdot \left( -4 \right) - 2 \cdot \left( 16 \right) + 3 \cdot \left( 7 \right) = -15\]

Fazit : Basierend auf den oben gezeigten Berechnungen wird festgestellt, dass die Determinante der Matrix \(\det A = \displaystyle -15\) ist.

Andere nützliche Matrixrechner, die Sie verwenden können

Von Hand durchgeführte Matrixberechnungen sind arbeitsintensiv, sodass Sie unsere linearen Algebra-Solvers nutzen können.

Zunächst können Sie diesen inversen Matrixrechner verwenden, um die Umkehrung einer Matrix zu berechnen, die Schritte zeigt, und Sie können dies entweder durch tun Adjoint -Methode oder durch Verwendung Rref -Redukion .