Weitere informationen zur normalisierung durch konvertierung in z-scores

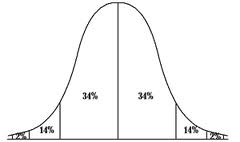
Das Konzept der Normalisierung von Scores oder Z-Score-Normalisierung entspricht der Berechnung der Z-Scores für alle in einem Datensatz enthaltenen Scores. Das bedeutet, dass wir für jeden \(X_i\)-Score in einem Datensatz den entsprechenden normalisierten Score (Z-Score) nach der folgenden Formel berechnen:

. \[ X_i = \frac{X_i - \mu}{\sigma}\]

Wenn der Mittelwert der Grundgesamtheit \(\mu\) oder die Standardabweichung der Grundgesamtheit \(\sigma\) nicht bekannt sind, approximieren wir sie, indem wir den Mittelwert der Stichprobe \(\bar X\) und die Standardabweichung der Stichprobe \(s\) berechnen.

Diese normalisierten Z-Scores reagieren auf eine Standardnormalverteilung und können mithilfe von Standardtabellen oder Rechentools wie Excel einfach berechnet werden.

Die notwendigkeit von z-scores

Warum brauchen wir normalisierte Werte? Normalisierte Werte bieten viele Vorteile: Erstens sind sie dimensionslos und eignen sich daher hervorragend für den Vergleich verschiedener Populationen. Zweitens ermöglichen sie eine klare Interpretation der Skalen, wie sie typischerweise in der Psychologie oder anderen Sozialwissenschaften verwendet wird.

Wenn Sie vollständige beschreibende Statistiken für Ihre Beispieldaten berechnen müssen, verwenden Sie diese vollständiger Rechner für beschreibende Statistiken oder wenn Sie dies verwenden Normaler Wahrscheinlichkeitsrechner um alles zu berechnen und grafisch darzustellen, was mit normalen Wahrscheinlichkeiten zusammenhängt, einschließlich Z-Score-Wahrscheinlichkeiten.