Algebra Tutorials

Der Binomialsatz

Der Binomialsatz ist einer der bekanntesten Sätze in der Algebra und hat eine Vielzahl von Anwendungen in den Bereichen Algebra, Wahrscheinlichkeit und Statistik. Es gibt eine schöne und prägnante Formel für das n an ^th Potenz der Summe zweier Werte: \((a+b)^n\)

Ich wurde zuerst 1665 von Sir Isaac Newton informell vorgestellt.

Viele andere bemerkenswerte Mathematiker haben sich nach Newton mit dem Binomialsatz befasst. Es war ein sehr attraktives Problem im 17. und 18. Jahrhundert.

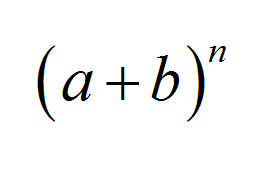
Die Formel für die Binomialerweiterung

Das Binomial-Theorem ist eine Ganzzahl, die eine sehr elegante und prägnante Formel liefert. Bevor wir uns mit der Formel befassen, lassen Sie uns einige Berechnungen durchführen. Zum Beispiel erhalten wir für \(n = 2\):

\[\large (a+b)^2 = (a+b) \times (a+b) = a(a+b) + b(a+b) = a^2 + ba + ab + b^2 \] \[\large = a^2 + 2ab + b^2 \]

Versuchen wir es jetzt mit \(n = 3\):

\[\large (a+b)^3 = (a+b)^2 \times (a+b) = (a^2 + 2ab+b^2)(a+b) \] \[\large = a^3 + 2a^2b + ab^2 + a^2b + 2ab^2 + b^3 \] \[\large = a^3 + 3a^2b + 3ab^2 + b^3\]

Lassen Sie uns zum Schluss mutig sein und es mit \(n = 4\) versuchen:

\[\large (a+b)^4 = (a+b)^3 \times (a+b) = (a^3 + 3a^2b + 3ab^2 + b^3)(a+b) \] \[\large = a^4 + 3a^3 b + 3a^2b^2 + ab^3 + a^3b + 3a^2b^2 + 3ab^3 + b^4 \] \[\large = a^4 + 4a^3b + 6 a^2 b^2 + 4a b^3 + b^4\]

Ok, das war mutig, oder? Sehen Sie dort irgendwelche Muster? Ich kann einige sehen. Zum Beispiel könnten wir für \(n = 2\) es auf 3 Begriffe vereinfachen. Für \(n = 3\) könnten wir es auf 4 Begriffe vereinfachen, und für \(n = 4\) könnten wir es auf 5 Begriffe vereinfachen. Im Allgemeinen erwarte ich, dass wir für die allgemeine Potenz von \(n\) \(n+1\) Begriffe haben werden

Weitere Muster? Nun, es gibt immer einen Begriff der Form \(a^l b^m\), und wir können sehen, dass die \(l\)- Potenzen abnehmen und die \(m\)- Potenzen zunehmen. Aber es gibt auch etwas Interessantes: Wenn Sie jeden Begriff überprüfen, ist die Summe der Potenzen immer \(n\). In der Tat werden Sie \(l + m = n\) für alle diese Begriffe überprüfen.

Für \(n = 2\) haben Sie beispielsweise den Begriff \(2 a b\). Die Potenz von \(a\) ist 1 und die Potenz von \(b\) ist 1 und die Summe der Potenzen ist \(1 + 1 = 2\). Oder Sie haben zum Beispiel für \(n = 4\) den Begriff \(6 a^2 b^2\), wobei die Potenz von \(a\) 2 und die Potenz von \(b\) 2 ist und die Summe der Potenzen \(2 + 2 = 4\) ist

Der allgemeine Binomialsatz

Jetzt sind wir bereit, den allgemeinen Ausdruck für den Binomialsatz zu geben. Bereit? Wir haben:

\[\large (a+b)^n = a^n + {n \choose 1} a^{n-1} b + {n \choose 2} a^{n-2} b^2 + ... + {n \choose n-1} a b^{n-1} + b^n \]

wobei der Begriff \({n \choose i}\) als "n wähle i" oder auch als "kombinatorischer Koeffizient" lautet und definiert ist als

\[\large \displaystyle {n \choose i}= \frac{n!}{i! \times (n-i)!}\]

Beispielsweise,

\[\large \displaystyle {5 \choose 2} = \frac{5!}{2! \times (5-2)!} = \frac{5!}{2! \times 3!} = \frac{120}{2 \times 6} = 10\]

Sie können dies verwenden kombinatorischer Ko Personenrechner um mehr darüber zu erfahren und zu üben, indem Sie alle gezeigten Schritte sehen.

Der allgemeine Binomialsatz unter Verwendung einer Summation

Die obige Summe, die den Binomialsatz definiert, verwendet die Notation durch Erweiterung, um die Begriffe verständlicher zu machen. Wie immer in Mathe versuchen wir, die Dinge kompakter zu gestalten, und der obige Ausdruck kann wie folgt zusammengefasst werden:

\[\large \displaystyle (a+b)^n = \sum_{i=0}^n {n \choose i} a^i b^{n-i} \]

Beachten Sie die Potenzen der Begriffe in der Erweiterung. Der allgemeine Begriff ist \(a^i b^{n-i}\) (mal eine Konstante). Die Summe der Potenzen ist \(i + (n-i) = n\). Die Summe der Potenzen ALLER Terme in der Erweiterung muss also \(n\) sein. Ist es nicht hübsch ???

BEISPIEL 1

Kann der Begriff \(x^3 y^2\) (mal eine Konstante) Teil der Erweiterung von \((x+y)^6\) sein? Warum?

ANTWORTEN:

Die Antwort ist nein. In diesem Fall \(n = 6\) und wir wissen aus dem Binomialsatz, dass die Summe der Potenzen der Terme \(x^l y^m\) in der Erweiterung gleich \(n\) sein muss. In diesem Fall \(l + m = 3 + 2 = 5\), was nicht mit \(n = 6\) identisch ist. Daher kann der Begriff \(x^3 y^2\) (mal eine Konstante) nicht Teil der Erweiterung von \((x+y)^6\) sein.

BEISPIEL 2

Erweitern Sie \((a-b)^3\) mit dem Binomialsatz.

ANTWORTEN:

Warten. Sie müssen denken "Sie haben mir gerade beigebracht, wie man \((a+b)^n\) erweitert, aber jetzt fragen Sie mich nach \((a-b)^n\). Warum sind Sie so grausam?" Warten Sie mal. Ich spiele dir keinen Streich.

Es gibt immer einen Trick (vergessen Sie diese Zeile nicht, sie erscheint häufig in Mathe).

Beachten Sie, dass \(a - b\) mit \(a + (-b)\) identisch ist.

Ahhhhhhh, also gilt immer noch der Binomialsatz. Also dann:

\[\large (a-b)^3 = (a+(-b))^3 = a^3 + {3 \choose 1} a^2 (-b) + {3 \choose 2} a (-b)^2 + (-b)^3 \] \[\large \displaystyle = a^3 - \frac{3!}{1! \times 2!} a^2 b + \frac{3!}{2! \times 1!} a b^2 -b^3 \] \[\large \displaystyle = a^3 - \frac{6}{1 \times 2} a^2 b + \frac{6}{2 \times 1} a b^2 -b^3 \] \[\large = a^3 - 3 a^2 b + 3 a b^2 -b^3 \]

Weitere Informationen zur Binomialerweiterung

Das Binomial-Theorem ist so wichtig, dass es in fast allen Kursen behandelt wird, einschließlich Algebra, Kalkül, Wahrscheinlichkeit und Statistik.

Es gibt einige Verallgemeinerungen wie die negative Binomialerweiterung, die den Rahmen dieses Tutorials sprengt.

Das Pascal-Dreieck

Manchmal bleiben die Schüler stecken, wenn sie die Konstanten (die kombinatorischen Koeffizienten) berechnen müssen, die in der Binomialerweiterung enthalten sind. Eine wirklich einfache Möglichkeit ist die Verwendung des Pascal-Dreiecks.

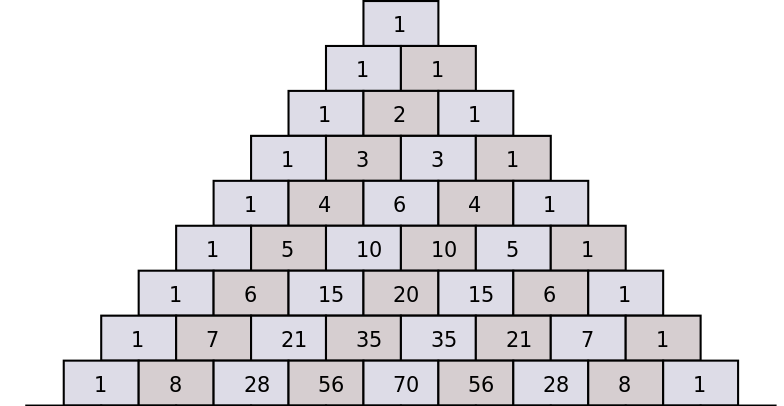
Das Pascal-Dreieck zeigt, wie die aufeinanderfolgenden Binomialkoeffizienten basierend auf den Koeffizienten des vorherigen Werts von \(n\) berechnet werden können, indem die beiden unmittelbar darüber liegenden Koeffizienten addiert werden.

Anwendungen

Die Binomialerweiterung hat mehrere Anwendungen in der Algebra und in der Wahrscheinlichkeitstheorie. In Probability basiert die Binomialverteilung beispielsweise auf dem Binomialsatz.

Betrachten Sie in der Tat eine Zahl \(0 \le p \le 1\). Dann \(p + (1-p) = 1\) und wir können den Binomialsatz verwenden:

\[\large \displaystyle 1 = 1^n = (p + (1-p))^n = \sum_{i=0}^n {n \choose i} p^i (1-p)^{n-i} \]

was bedeutet, dass

\[\large \displaystyle \sum_{i=0}^n {n \choose i} p^i (1-p)^{n-i} = 1 \]

Es stellt sich heraus, dass jeder der Begriffe \({n \choose i} p^i (1-p)^{n-i}\) eine Wahrscheinlichkeit darstellt. Darüber hinaus haben wir:

\[\large \Pr(X = i) = {n \choose i} p^i (1-p)^{n-i} = 1 \]

Dabei ist \(X\) die Anzahl der Erfolge nach \(n\) Versuchen, wenn die Erfolgswahrscheinlichkeit jedes Versuchs \(p\) beträgt. Die Variable \(X\) wird als binomische Zufallsvariable bezeichnet.