Como funciona uma calculadora de regressão logarítmica

Esta calculadora permitirá que você estime uma regressão logarítmica para dados de amostra fornecidos na planilha de entrada de dados correspondente.

Quando dados válidos são fornecidos (nesse caso, a variável X só pode assumir valores positivos), depois de clicar em "Calcular", você obterá uma execução das etapas envolvidas no processo, bem como um gráfico de dispersão que mostrará a qualidade do ajuste.

Observe que quando os dados são dimensionalmente válidos, você sempre pode executar uma regressão logarítmica, mas isso não significa que os resultados serão de boa qualidade, pelo menos em termos de ajuste.

Ferramentas e calculadoras para regressão logarítmica

Existem diferentes ferramentas que você pode usar para estimar sua regressão logarítmica. Em teoria, você pode fazer as coisas manualmente, usando uma transformação de log usando uma calculadora comum talvez (mesmo aquelas que vêm com seu telefone), e então usar uma equação de mínimos quadrados auxiliar para encontrar o modelo de log, que é

\[ Y = a + b \ln(X) + \varepsilon \]

Certamente, a abordagem de fazer isso manualmente pode ser tediosa e propensa a erros, para dizer o mínimo. É por isso que é uma opção muito boa usar isso Calculadora de Regressão Logarítmica , porque ele faz todo o trabalho para você e mostra todos os passos

Existem outras ferramentas, como aplicativos para celulares, que supostamente fazem todos os tipos de regressão, mas você precisa tentar e ver, porque isso pode ser uma situação de tentativa e erro.

Etapas para executar uma regressão logarítmica

• Passo 1: Liste a variável independente (X) e a variável dependente (Y) claramente e certifique-se de que ambas as variáveis tenham o mesmo tamanho de amostra
• Passo 2: Certifique-se de que seus valores de X sejam positivos, caso contrário, você não poderá executar a regressão
• Etapa 3: Construa uma nova variável independente X* = ln(X) aplicando a transformação de logaritmo natural
• Passo 4: Agora você executa uma análise de regressão linear regular para X* versus Y

Uma coisa a ter em mente é que é totalmente aconselhável usar uma calculadora ou software para obter estatísticas de diagnóstico que o ajudarão a avaliar se faz sentido ou não usar a calculadora modelo de regressão logarítmica .

Usando o excel vs calculadoras de regressão logarítmica dedicadas

O Excel desempenha um papel importante ao ajudar você a conduzir análises estatísticas básicas: ele fornece uma interface limpa e comprovada para executar testes básicos, incluindo o cálculo de regressão logarítmica.

O principal problema com o Excel é que ele não fornece a você o passo de soluções. Isso pode ajudar com o advento de frameworks de IA como o Copilot, que provavelmente dotaria o Excel com passos descritivos do cálculo.

Compreendendo e interpretando os resultados da calculadora de regressão

Como qualquer outro Análise de regressão , para o caso logarítmico não é diferente, pois você dará uma olhada nas estatísticas de ajuste do modelo, como F-estatísticas para testar a significância do modelo em geral e Estatística t para significância individual dos preditores .

Além disso, você provavelmente vai querer dar uma olhada na variação e no erro explicados, e o Coeficientes R^2 e R^2 ajustado , que fornecerá estimativas da variação explicada da variável dependente pelo modelo.

Exemplos de regressão logarítmica

Considere as variáveis

X: 1, 2, 3, 4, 5

E: 15, 25, 28, 29, 30

Estimar um modelo de regressão logarítmica.

Solução:

Os seguintes dados para as variáveis X e Y são fornecidos para construir um modelo de regressão logarítmica:

X	E
1	15
2	25
3	28
4	29
5	30

A variável independente que usaremos é o logaritmo natural de X, e a variável dependente é Y. Para calcular os coeficientes de regressão para esta regressão auxiliar, a seguinte tabela precisa ser usada:

	X	Z = em(X)	E	\(Z \cdot Y\)	\(Z^2\)	\(Y^2\)
	1	0	15	0	0	225
	2	0.69	25	17.33	0.48	625
	3	1.1	28	30.76	1.21	784
	4	1.39	29	40.2	1.92	841
	5	1.61	30	48.28	2.59	900
Sum =	15	4.79	127	136.58	6.2	3375

Com base na tabela acima, calcula-se o seguinte:

\[\bar Z = \frac{1}{n} \sum_{i=1}^{n} Z_i = \frac{ 4.787491742782}{ 5} = 0.957\]\[\bar Y = \frac{1}{n} \sum_{i=1}^{n} Y_i = \frac{ 127}{ 5} = 25.4\]\[\large SS_{ZZ} = \sum_{i=1}^{n} Z_i^2 - \displaystyle\frac{1}{n}\left(\sum_{i=1}^{n} Z_i\right)^2 = 6.2 - 4.787^2/5 = 1.615\]\[\large SS_{YY} = \sum_{i=1}^{n} Y_i^2 - \displaystyle\frac{1}{n}\left(\sum_{i=1}^{n} Y_i\right)^2 = 3375 - 127^2/5 = 149.2\]\[\large SS_{ZY} = \sum_{i=1}^{n} Z_i Y_i - \displaystyle\frac{1}{n}\left(\sum_{i=1}^{n} Z_i\right) \left(\sum_{i=1}^{n} Y_i\right) = 136.575 - 4.787 \times 127/5 = 14.973\]

Portanto, com base nos cálculos acima, os coeficientes de regressão (a inclinação \(m\) e a interceptação y \(n\)) são obtidos da seguinte forma:

\[m = \frac{SS_{ZY}}{SS_{ZZ}} = \frac{ 14.973}{ 1.615} = 9.2685\] \[n = \bar Y - \bar Z \cdot m = 25.4 - 0.957 \times 9.2685 = 16.5254\]

Portanto, descobrimos que a equação de regressão é:

\[\text{ Y} = 16.5254 + 9.2685 \text{ Z}\]

Mas como a variável auxiliar \(Z = \ln(X)\), concluímos que a equação de regressão logarítmica é:

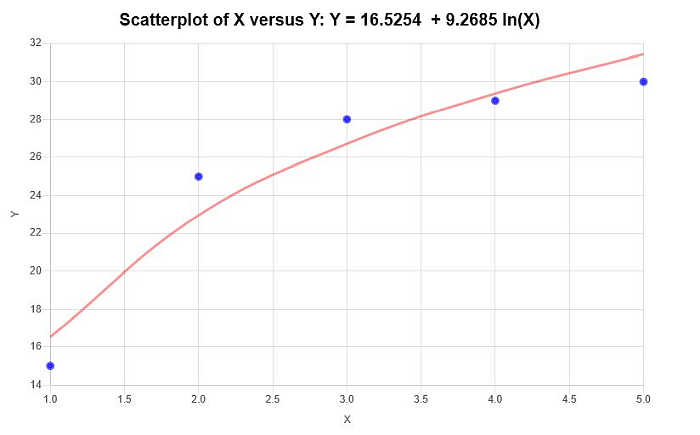
\[\text{ Y} = 16.5254 + 9.2685 \ln(X)\]

Portanto, com base nas informações fornecidas acima, obtém-se o seguinte gráfico de dispersão e gráfico de regressão:

Mais calculadoras estatísticas

Você também pode estar interessado em computando uma regressão exponencial , ou trabalhando as sutilezas de um regressão polinomial , todos os quais se aplicam em diferentes contextos, com base no comportamento dos dados da amostra observados.

Provavelmente você vai querer construir um gráfico de dispersão para avaliar o comportamento empírico dos dados e pré-avaliar se uma regressão logarítmica se aplica em vez de um tipo diferente de regressão.