Mais sobre esta ferramenta calculadora de linhas paralelas.

Geometricamente falando, duas linhas são paralelas quando não se cruzam, ou são potencialmente a mesma linha. Então, se você grafe as duas linhas , você verá visualmente que eles não se cruzam. Mas isso pode ser complicado.

Mas, naturalmente, existem maneiras algébricas de avaliar se duas linhas são paralelas ou não. Uma das maneiras mais simples é usar o critério de inclinação.

Como determinar se duas linhas são paralelas?

Existem algumas maneiras:

1. Graficamente: Dê uma olhada no gráfico, e se as linhas não se cruzam, então as linhas são paralelas
2. Algebricamente: Calcule a inclinação para cada uma das linhas. Se eles têm a mesma inclinação, as linhas são paralelas

A vantagem do método gráfico é que ele é simples e envolve apenas dar uma olhada no gráfico, mas naturalmente, para isso, você precisa construir os gráficos.

Uma desvantagem do método gráfico é que seus olhos podem enganá-lo. Pode parecer que o gráfico de linhas não se cruzam, mas talvez você não esteja representando graficamente uma porção grande o suficiente da linha.

Uma vantagem do método algébrico é que ele é inequívoco. Se as inclinações coincidirem, as linhas são paralelas, e se não coincidirem, as linhas não são paralelas.

A única desvantagem do método algébrico é que você precisa fazer o trabalho de cálculo da inclinação .

Equação de retas paralelas

Observe que as linhas paralelas terão a mesma inclinação. Então, se a equação de uma reta é \(y = a x + b\), qual é a equação da reta paralela?

Primeiro, não há uma linha paralela, na verdade existem infinitas linhas paralelas, e a equação é \(y = a x + c\), para qualquer \(c\).

Como podemos ver, \(y = a x + b\) e \(y = a x + c\) ambos têm uma inclinação igual a "a", então eles são paralelos.

Se você não tiver as linhas já em formato de interceptação de inclinação , você pode sempre Resolva para e ou Resolva para x é que você quer inverter os eixos.

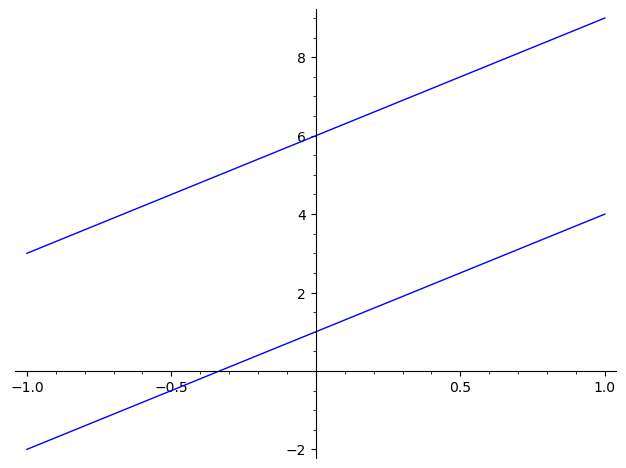
O critério de inclinação

Duas retas são paralelas se tiverem a mesma inclinação. Então essa é a maneira mais fácil de determinar se duas linhas são paralelas, você simplesmente calcule a inclinação de ambas as linhas e verifique se são iguais ou não.

Uma exceção é o caso de duas linhas verticais, que são paralelas, embora não possamos comparar as inclinações porque são indefinidas.

Se você tem algo como o forma de intercepção de encostas das linhas já dadas, você pode avaliar diretamente se as linhas são paralelas ou não. Caso contrário, você precisará da etapa extra de calcular as inclinações antes de compará-las.

Interpretação geométrica do gráfico de duas linhas paralelas

Duas retas paralelas correspondem a uma Sistema de equações sem soluções (ou infinitas soluções), onde cada equação representa uma linha.

Além disso, quando as linhas não são paralelas, elas se cruzam em um ponto e em apenas um ponto, o que corresponde a uma Sistema de equações com uma solução única.

Exemplo

Determine se as linhas \(2x + 3y = 1\) e \(x + y = 3\) são paralelas.

Resposta:

Primeira linha: Coloque a primeira equação na forma de interceptação de inclinação

Foi-nos fornecida a seguinte equação:

\[\displaystyle 2x+3y=1\]

Colocando \(y\) no lado esquerdo e \(x\) e a constante no lado direito obtemos

\[\displaystyle 3y = -2x +1\]

Agora, resolvendo para \(y\), obtém-se o seguinte

\[\displaystyle y=\frac{-2}{3}x+\frac{1}{3}\]

e simplificando todos os termos que precisam de simplificação, finalmente obtemos o seguinte

\[\displaystyle y=-\frac{2}{3}x+\frac{1}{3}\]

Segunda Linha: Coloque a segunda equação na forma de interceptação de inclinação

Foi-nos fornecida a seguinte equação:

\[\displaystyle x+y=3\]

Colocando \(y\) no lado esquerdo e \(x\) e a constante no lado direito obtemos

\[\displaystyle y = -x +3\]

Analisar e comparar inclinações

Com base nessas informações, descobrimos que a inclinação da primeira linha é \(m_1 = -\frac{2}{3}\) e a inclinação da segunda linha também é \(m_2 = -1\), que são desiguais, então as linhas NÃO são paralelas.

Observe que se a perpendicularidade é o que você está procurando, você pode usar isso calculadora de linhas perpendiculares . Por definição, as linhas perpendiculares não são paralelas, porque as linhas perpendiculares SEMPRE têm inclinações diferentes.