Calculadora de inclinações perpendiculares
Instruções: Utilize esta ferramenta gráfica para traçar o achado, passo a passo, a inclinação de uma linha perpendicular a uma linha que tem uma determinada inclinação. Por favor, indique a inclinação da sua linha (qualquer expressão numérica válida).
Mais sobre esta calculadora de inclinações perpendiculares.
Muitas vezes precisamos de lidar com linhas e outras linhas que são perpendiculares a elas. A perpendicularidade tem a ver com ter um 90 o ângulo entre as linhas.
Mas a questão é, como é que relacionamos isto perpendicularidade de duas linhas com as inclinações das duas linhas?
A resposta é simples: duas linhas com declives <\(m_1\) e \(m_2\) são perpendiculares se e só se
\[m_1 \cdot m_2 = -1\]
Como se calcula a inclinação perpendicular?
A resposta está aí mesmo. Se sabe <\(m_1\), então tudo o que precisa de fazer é resolver a inclinação para a linha que é perpendicular, <\(m_2\), por isso obtemos o seguinte fórmula para a inclinação perpendicular :
\[\displaystyle m_2 = -\frac{1}{m_1}\]que é a fórmula para a inclinação perpendicular a partir do declive da linha .
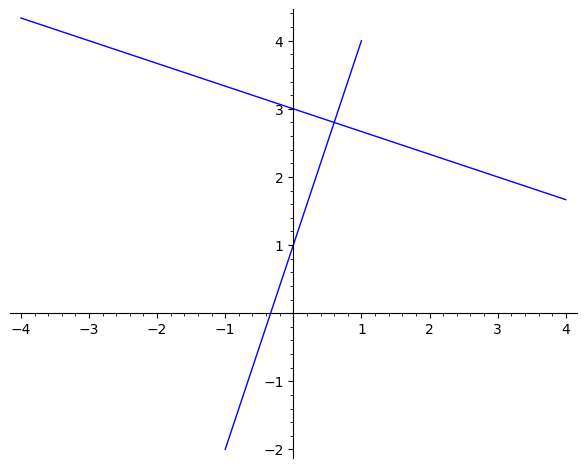
Como se calcula a inclinação perpendicular se se tiver a equação de uma linha?
Nesse caso, o primeiro que precisa de fazer é converter a equação em forma de intercepção de inclinações . Uma vez conhecida a inclinação, será possível utilizar a fórmula apresentada acima.
Em última análise, uma vez que se tenha a inclinação da linha perpendicular, sabendo que um ponto dessa linha perpendicular passa, é possível calcular a equação da linha perpendicular .
Exemplo: cálculo do declive de uma linha perpendicular
Considerar a linha com a equação <\(x + 3y = 2)\)>. Encontrar a inclinação da linha perpendicular à linha dada.
Solução: A equação pode ser reescrita como: \[3y = -x + 2\]>>>XYZB>>> Assim, a inclinação dada da linha fornecida é \(m = \displaystyle -\frac{ 1}{ 3}\), e precisamos de calcular a inclinação perpendicular.
A fórmula necessária para calcular a inclinação perpendicular, <\(m_{\perp}\), é:
\[m_{\perp} = \displaystyle -\frac{1}{m}\]Ao ligar o valor de \(m = -\frac{ 1}{ 3}\) na fórmula, verificamos que a inclinação perpendicular é
\[m_{\perp} = \displaystyle -\frac{1}{m} = \displaystyle -\frac{1}{-\frac{ 1}{ 3}} = 3\]Portanto, concluímos que a inclinação perpendicular é \(m_{\perp} = 3 \)>