Calculando a elasticidade-preço da demanda a partir de dados de amostra

Use esta calculadora para estimar a elasticidade-preço da demanda com base em dados de amostra de preço e quantidade demandada que você fornece.

Você precisará fornecer dados de amostra válidos, em termos de ambas as amostras (preço e quantidade demandada) sendo valores positivos. Depois de ter seus dados colados na planilha, você pode clicar em "Calcular" para obter todas as etapas mostradas.

Observe que essa abordagem requer que os dados sigam um padrão específico que se adapta a um modelo log-log, onde \(\ln(P)\) e \(\ln(Q)\) são usadas como variáveis auxiliares para conduzir um modelo de regressão linear.

Calculando a elasticidade de preço a partir de dados de amostra

Para calcular a elasticidade do preço, você precisará estimar o seguinte modelo auxiliar:

\[\displaystyle \ln(Q) = a + b \ln(P) \]

Observe que isso corresponde a um modelo de regressão linear regular com as variáveis originais preço e quantidade sendo transformadas em logaritmo. É por isso que exigimos que ambas as variáveis sejam estritamente positivas.

Quais são os passos para calcular a elasticidade?

• Passo 1: Identifique os dados da amostra para as variáveis fornecidas para preço (P) e quantidade (Q)
• Passo 2: Certifique-se de que ambas as amostras tenham o tamanho de amostra e que AMBAS sejam positivas, caso contrário, você não conseguirá fazer o cálculo
• Etapa 3: Transformar logaritmicamente ambas as variáveis: calcular ln(X) e ln(Y)
• Passo 4: Realizar uma regressão linear auxiliar para as variáveis ln(X) e ln(Y), onde ln(X) é a variável independente e ln(Y) é a variável dependente
• Passo 5: O coeficiente de inclinação encontrado para esta regressão auxiliar é a elasticidade-preço da demanda por esses dados

O passo crucial então é a transformação logarítmica dos dados, que nos permite calcular a elasticidade com base nos resultados de uma regressão linear, tornando os resultados encontrados altamente interpretáveis.

Compreendendo a elasticidade de preço

Por definição, a elasticidade de preço é definida usando a seguinte fórmula:

\[ \varepsilon = \displaystyle \frac{\% \Delta Q }{\% \Delta P} \]

Isso indica que, entre outras coisas, podemos prever a variação percentual da quantidade demandada usando a seguinte expressão:

\[ \% \Delta Q = \varepsilon \cdot \% \Delta P \]

Isso indica que a mudança percentual em Q é a mesma que a mudança percentual em P multiplicada pela elasticidade. É importante notar que essa definição se aplica pontualmente : isto é, a elasticidade não precisa ser constante ao longo da curva de demanda. Embora possa, e nesta calculadora tal suposição é feita.

Interpretando coeficientes de elasticidade de preço

Como vimos na seção anterior, a elasticidade \(\varepsilon\) simplesmente corresponde ao coeficiente de inclinação da regressão log-transformada auxiliar. Mas também, tem uma interpretação de mudança marginal muito interessante:

• Para uma mudança extra de 1% no preço, a quantidade demandada muda em \(\varepsilon \%\)

É precisamente isso que é requerido e implícito pela fórmula de elasticidade. Observe que esta calculadora estima um modelo que assume que os dados seguem um padrão que é propício a uma elasticidade constante, o que não é o caso de uma função de demanda linear, por exemplo.

Fatores que influenciam a elasticidade do preço

Elasticidade é um reflexo da reação dos consumidores a mudanças no preço. Tipicamente, a elasticidade é negativa: se o preço de um bem aumenta, o comprador provavelmente comprará menos, pelo menos se tivermos um bem normal.

Uma elasticidade maior que 1 em valor absoluto (menor que -1) é considerada associada a uma reação elástica ao preço, enquanto uma elasticidade entre 0 e 1 em valor absoluto (entre -1 e 0) é considerada associada a uma reação inelástica ao preço.

A teoria econômica prevê que diferentes fatores afetarão a elasticidade-preço da demanda. Por exemplo, ausência ou escassez de substitutos levará a uma elasticidade maior em valores absolutos.

Cálculo de elasticidade de amostra: usando dados de amostra

Calcule a elasticidade a partir dos seguintes dados de amostra:

P	Pq
1	10
2	13.4
3	15.8
4	21.2
5	26.7
6	40.1

Solução :Para encontrar a elasticidade-preço da demanda a partir desses dados, precisamos construir um modelo de regressão log-log, onde a variável independente que usaremos é \(ln(P)\), e a variável dependente é o logaritmo natural de \(ln(Q)\)

Para calcular os coeficientes de regressão para esta regressão auxiliar, a seguinte tabela precisa ser usada:

	P	Z = em(P)	Pq	W = em(Q)	\(Z \cdot W\)	\(Z^2\)	\(W^2\)
	1	0	10	2.303	0	0	5.302
	2	0.69	13.4	2.595	1.8	0.48	6.735
	3	1.1	15.8	2.76	3.03	1.21	7.618
	4	1.39	21.2	3.054	4.23	1.92	9.327
	5	1.61	26.7	3.285	5.29	2.59	10.789
	6	1.79	40.1	3.691	6.61	3.21	13.626
Sum =	21	6.58	127.2	17.688	20.97	9.41	53.397

Com base na tabela acima, calcula-se o seguinte:

\[\bar Z = \frac{1}{n} \sum_{i=1}^{n} Z_i = \frac{ 6.579}{ 6} = 1.097\]\[\bar W = \frac{1}{n} \sum_{i=1}^{n} Y_i = \frac{ 17.688}{ 6} = 2.948\] \[\large SS_{ZZ} = \sum_{i=1}^{n} Z_i^2 - \displaystyle\frac{1}{n}\left(\sum_{i=1}^{n} Z_i\right)^2 = 9.41 - 6.579^2/6 = 2.195\] \[\large SS_{WW} = \sum_{i=1}^{n} W_i^2 - \displaystyle\frac{1}{n}\left(\sum_{i=1}^{n} W_i\right)^2 = 53.397 - 17.688^2/6 = 1.254\] \[\large SS_{ZW} = \sum_{i=1}^{n} Z_i W_i - \displaystyle\frac{1}{n}\left(\sum_{i=1}^{n} Z_i\right) \left(\sum_{i=1}^{n} W_i\right) = 20.965 - 6.579 \times 17.688/6 = 1.57\]

Portanto, com base nos cálculos acima, os coeficientes de regressão (a inclinação \(m\) e a interceptação y \(n\)) são obtidos da seguinte forma:

\[m = \frac{SS_{ZW}}{SS_{ZZ}} = \frac{ 1.57}{ 2.195} = 0.715\]\[n = \bar W - \bar Z \cdot m = 2.948 - 1.097 \times 0.715 = 2.1639\]

Portanto, descobrimos que a equação de regressão é:

\[W = 2.1639 + 0.715 \text{ Z}\]

Mas como as variáveis auxiliares são \(Z = \ln(X)\) e \(W = \ln(Y)\), concluímos que a equação de regressão log-log é:

\[\ln(Q) = 2.1639 + 0.715 \ln(P)\]

Portanto, com base nas informações fornecidas acima, obtém-se o seguinte gráfico de dispersão e gráfico de regressão:

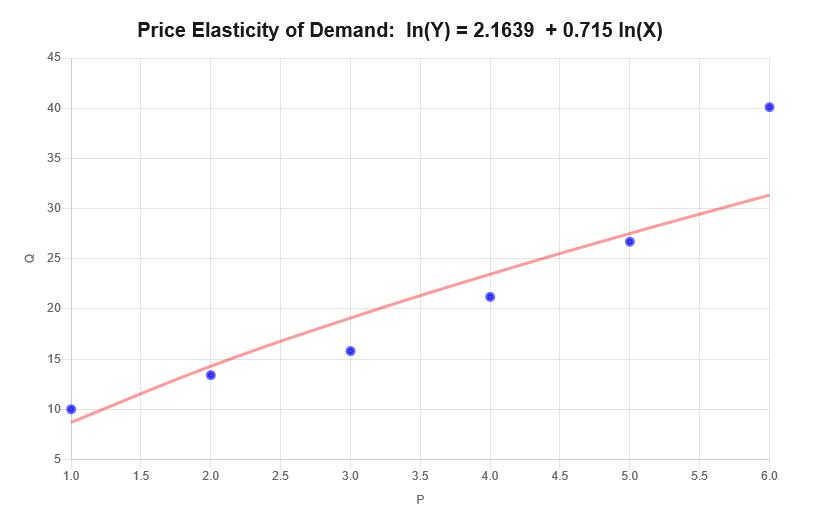
Interpretação

A elasticidade neste caso corresponde ao coeficiente de inclinação dos dados fornecidos, o que significa \(\varepsilon = 0.715 \), que pode ser interpretado da seguinte forma:

• Para um aumento de 1% no preço, há um aumento médio de 0,715% na quantidade demandada.

Calculadoras mais interessantes

Estimar modelos a partir de dados de amostra é uma habilidade crucial necessária tanto em Estatística quanto em Economia. Usar dados de amostra para calcular um modelo de regressão é uma das aplicações mais comuns do uso de dados de amostra para construção de modelos.

Mas é frequente que um modelo linear regular não se ajuste suficientemente bem aos dados, para o qual precisamos tentar diferentes estruturas funcionais. Por exemplo, poderíamos potencialmente estimar uma Regressão Log-Log , um regressão logarítmica ou um regressão polinomial , só para citar alguns, que poderiam ser mais bem-sucedidos em explicar a variação na variável dependente do que a regressão regular.

A opção de calculando a elasticidade a partir de dados de amostra é usado principalmente em um ambiente exploratório. Na maioria das vezes, o a elasticidade é calculada diretamente a partir da função de demanda , quando disponível. Em outras circunstâncias, a elasticidade é estimada a partir de um par de pontos de preço-demanda usando o fórmula de arco-elasticidade .