Questão 1: As fórmulas para a menor linha quadrada foram encontradas resolvendo o sistema de equações

\[nb+m\left( \sum{x} \right)=\sum{y}\]

\[b\left( \sum{x} \right)+m\left( \sum{x^2} \right)=\sum{xy}\]

Resolva essas equações para b e m para mostrar que

\[\begin{align} & m=\frac{n\left( \sum{xy} \right)-\left( \sum{x} \right)\left( \sum{y} \right)}{n\left(\sum{{{x}^{2}}} \right)-{{\left( \sum{x} \right)}^{2}}} \\ & b=\frac{\sum{y-m\left( \sum{x}\right)}}{n} \\ \end{align}\]

Solução: A partir de

\[ nb+m\left( \sum{x} \right)=\sum{y}\]

\[b\left( \sum{x} \right)+m\left( \sum{x^2} \right)=\sum{xy}\]

temos duas equações e duas incógnitas (m e b)

Conseguimos isso multiplicando a primeira equação por \(\left( \sum{x} \right)\) e a segunda por -n, obtemos

\[\begin{align} & nb\left( \sum{x} \right)+m{{\left( \sum{x} \right)}^{2}}=\left( \sum{y}\right)\left(\sum{x} \right) \\ & -nb\left( \sum{x} \right)-mn\left( {{\sum{x}}^{2}}\right)=n\sum{xy} \\ \end{align}\]

e agora adicionando estes:

\[m\left( {{\left( \sum{x} \right)}^{2}}-n\left( {{\sum{x}}^{2}} \right) \right)=\left( \sum{x} \right)\left(\sum{y} \right)-n\left( \sum{xy} \right)\]

\[\Rightarrow \,\,\,\,m=\frac{\left( \sum{x} \right)\left( \sum{y} \right)-n\left( \sum{xy} \right)}{{{\left( \sum{x} \right)}^{2}}-n\left( {{\sum{x}}^{2}} \right)}=\frac{n\left( \sum{xy} \right)-\left( \sum{x} \right)\left( \sum{y} \right)}{n\left( {{\sum{x}}^{2}} \right)-{{\left( \sum{x} \right)}^{2}}}\]

Agora, a partir desta equação:

\[nb+m\left( \sum{x} \right)=\left( \sum{y} \right)\]

nós podemos resolver para b :

\[nb+m\left( \sum{x} \right)=\left( \sum{y} \right)\,\,\Rightarrow \,\,\,nb=\left( \sum{y} \right)-m\left( \sum{x} \right)\,\Rightarrow \,\,\,b=\frac{\left( \sum{y} \right)-m\left( \sum{x} \right)}{n}\]

Questão 2: Determine o coeficiente de correlação e faça um gráfico da linha de regressão com o coeficiente de regressão para o seguinte conjunto de dados.

Incêndios florestais e hectares queimados. O número de incêndios e o número de hectares queimados são os seguintes

Incêndios (x)	72	69	58	47	84	62	57	45
Acres (y)	62	41	19	26	51	15	30	15

Solução: (a) O seguinte gráfico de dispersão é obtido:

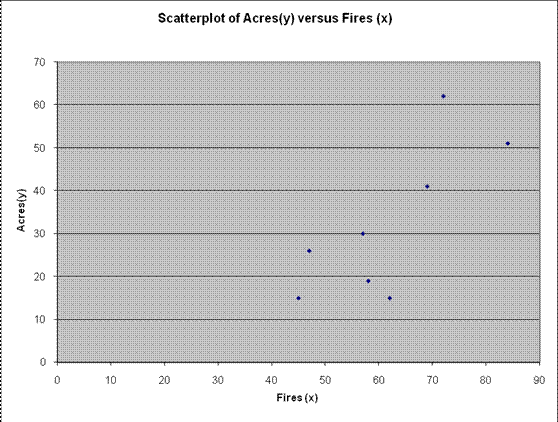
Com base no gráfico de dispersão acima, observamos que existe um grau moderado a forte de associação linear positiva.

(b) Por outro lado, temos a seguinte tabela que mostra os cálculos necessários para calcular a correlação de Pearson: Obtemos

A correlação de Pearson r é calculada como

\[r = \frac{n\sum\limits_{i=1}^{n}{{{x}_{i}}{{y}_{i}}}-\left( \sum\limits_{i=1}^{n}{{{x}_{i}}} \right)\left( \sum\limits_{i=1}^{n}{{{y}_{i}}} \right)}{\sqrt{n\left( \sum\limits_{i=1}^{n}{x_{i}^{2}} \right)-{{\left( \sum\limits_{i=1}^{n}{{{x}_{i}}} \right)}^{2}}}\sqrt{n\left( \sum\limits_{i=1}^{n}{y_{i}^{2}} \right)-{{\left( \sum\limits_{i=1}^{n}{{{y}_{i}}} \right)}^{2}}}} = \frac{8 \times {17216}-{494}\times {259}}{\sqrt{8\times {31692}-{494}^{2}}\sqrt{8\times 10513-{259}^{2}}}\]

\[=0.7692\]

(c) O coeficiente de determinação é

\[{{r}^{2}}={0.7692}^{2}= {0.5917}\]

o que significa que 59,17% da variação em Acres (y) é explicada por Fogos (x).

(d) Os coeficientes de regressão são calculados

\[b=\frac{n\left( \sum\limits_{i=1}^{n}{{{x}_{i}}{{y}_{i}}} \right)-\left( \sum\limits_{i=1}^{n}{{{x}_{i}}} \right)\left( \sum\limits_{i=1}^{n}{{{y}_{i}}} \right)}{n\left( \sum\limits_{i=1}^{n}{x_{i}^{2}} \right)-{{\left( \sum\limits_{i=1}^{n}{{{x}_{i}}} \right)}^{2}}}=\frac{8 \times {17216}-{494}\times {259}}{8 \times {31692}-{494}^{2}}= 1.0297\]

and

\[a=\bar{y}-b \bar{x}={32.375}{+} {1.0297}\,\cdot \, {61.75} = {-31.208}\]

Isso significa que a equação de regressão é

\[\hat{y}= {-31.208}{+}{1.0297}\,x\]

Graphically:

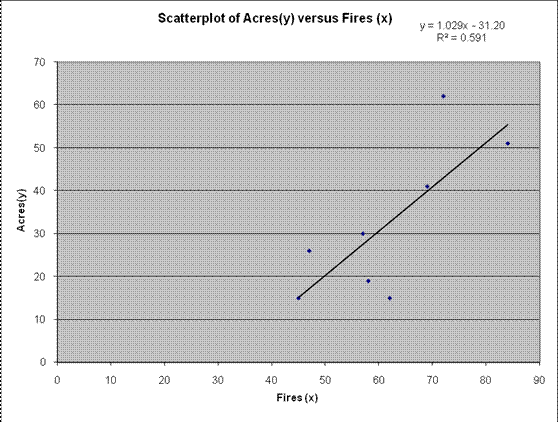
Questão 3: Você conduziu um estudo para determinar se o tempo médio gasto no laboratório de informática a cada semana e a nota do curso em um curso de informática estavam correlacionados. Usando os dados fornecidos a seguir, que conclusão você tiraria sobre esse assunto?

student	# hours in lab	Course Grade
1	20	96
2	11	51
3	16	62
4	13	58
5	89
6	15	81
7	10	46
8	10	51

Solução: A tabela a seguir mostra os cálculos necessários para calcular Pearson Correr : Nós temos

A correlação de Pearson r é calculada como

\[r = \frac{n\sum\limits_{i=1}^{n}{{{x}_{i}}{{y}_{i}}}-\left( \sum\limits_{i=1}^{n}{{{x}_{i}}} \right)\left( \sum\limits_{i=1}^{n}{{{y}_{i}}} \right)}{\sqrt{n\left( \sum\limits_{i=1}^{n}{x_{i}^{2}} \right)-{{\left( \sum\limits_{i=1}^{n}{{{x}_{i}}} \right)}^{2}}}\sqrt{n\left( \sum\limits_{i=1}^{n}{y_{i}^{2}} \right)-{{\left( \sum\limits_{i=1}^{n}{{{y}_{i}}} \right)}^{2}}}} = \frac{8 \times {7925}-{112}\times {534}}{\sqrt{8\times {1660}-{112}^{2}}\sqrt{8\times 38224-{534}^{2}}}\]

\[=0.9217\]

Queremos testar a significância do coeficiente de correlação. Mais especificamente, queremos testar

\[\begin{align}{{H}_{0}}:\rho {=} 0 \\ {{H}_{A}}:\rho {\ne} 0 \\ \end{align}\]

Para testar a hipótese nula, definiu um teste t. A estatística t é calculada como

\[t= r \sqrt{\frac{n-2}{1-{{r}^{2}}}}= {0.9217} \times \sqrt{\frac{6}{1-{0.9217}^2}}= {5.8198}\]

O valor p de duas caudas para este teste é válido como

\[p=\Pr \left( |{{t}_{6}}|>5.8198 \right)=0.0011\]

Desde \(p = 0.0011 {<} 0.05\) , e isso significa que rejeitamos a hipótese nula H ₀ .

Portanto, existem evidências para apoiar uma afirmação de que a correlação entre o número de horas no laboratório e a nota do curso é diferente de zero.