Derivate trigonometriche inverse

Con questa calcolatrice sarai in grado di calcolare le derivate di funzioni trigonometriche inverse, mostrando tutti i passaggi del processo.

L'idea è che la funzione che fornisci contenga una funzione trigonometrica inversa, ad esempio f(x) = x^2/arctan(x+1), solo per fare un esempio.

Quando sei pronto e hai finito di digitare la funzione che devi differenziare, fai clic sul pulsante "Calcola" per vedere tutti i passaggi del processo e i calcoli.

L'idea di calcolo delle derivate delle funzioni trigonometriche inverse è naturale, e vedremo nei prossimi paragrafi che possono essere derivate direttamente dalla derivati trigonometrici che conosci.

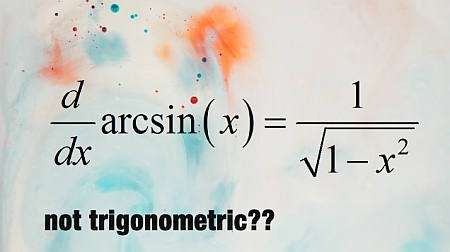
Funzioni trigonometriche inverse

In termini semplici, le funzioni trigonometriche inverse sono quelle funzioni che valutandole alla funzione trigonometrica corrispondente, portano all'identità. Ad esempio, se consideriamo la funzione \(\sin(x)\), la sua funzione inversa è \(\arcsin(x)\), e questa inversa ha la proprietà che

\[\sin(\arcsin(x)) = x \]

così come

\[\arcsin(\sin(x)) = x \]

per tutti i \(x\) su un certo intervallo. Quindi, rigorosamente, \(\arcsin(x)\) è la funzione inversa di \(\sin(x)\) da un punto di vista algebrico. E lo stesso vale per le altre funzioni trigonometriche inverse e le corrispondenti funzioni trigonometriche.

Calcolo delle derivate trigonometriche inverse

Quindi, se \(f\) è una funzione, e ha un inverso \(f^{-1}\), allora abbiamo che

\[f^{-1}(f(x)) = x\]

per tutti i \(x\). Quindi, se distinguiamo entrambi i lati dell'uguaglianza e usiamo la regola della catena sul lato sinistro, otteniamo

\[ \displaystyle (f^{-1})'(f(x))f'(x) = 1\] \[ \displaystyle (f^{-1})'(f(x)) = \frac{1}{f'(x)}\]

Ora, se impostiamo \(y = f(x)\), allora \(x = f^{-1}(y)\), che porta a

\[ \displaystyle (f^{-1})'(y) = \frac{1}{f'(f^{-1}(y))}\] \[ \Rightarrow \displaystyle (f^{-1})'(x) = \frac{1}{f'(f^{-1}(x))}\]

Come lo usiamo per le funzioni trigonometriche inverse? Assumi \(f(x) = \sin(x)\) e \(f^{-1}(x) = \arcsin(x)\). Quindi, in base alla relazione generale tra la derivata di una funzione e la derivata della sua inversa, otteniamo

\[ \displaystyle \frac{d}{dx} \arcsin(x) = \frac{1}{\frac{d}{dx}\sin (\arcsin(x))}\] \[ \Rightarrow \displaystyle \frac{d}{dx} \arcsin(x) = \frac{1}{\cos(\arcsin(x))}\]

Ma un bel trucco geometrico ce lo dice

\[\cos(\arcsin(x)) = \sqrt{1 - \sin^2(\arcsin(x))} = \sqrt{1 - x^2} \]

il che lo implica

\[ \displaystyle \frac{d}{dx} \arcsin(x) = \frac{1}{ \sqrt{1 - x^2}}\]

Il resto delle derivate trigonometriche inverse si ottengono con un argomento simile.

Quali sono le 6 funzioni trigonometriche inverse di base?

• #1: \( \displaystyle \frac{d}{dx} \arcsin(x) = \frac{1}{ \sqrt{1 - x^2}}\)
• #2: \( \displaystyle \frac{d}{dx} \arccos(x) = -\frac{1}{ \sqrt{1 - x^2}}\)
• #3: \( \displaystyle \frac{d}{dx} \arctan(x) = \frac{1}{1+x^2}\)
• #4: \( \displaystyle \frac{d}{dx} \operatorname{arccot}(x) = -\frac{1}{1+x^2}\)
• #5: \( \displaystyle \frac{d}{dx} \operatorname{arcsec}(x) = \frac{1}{x \sqrt{x^2-1}}\)
• #6: \( \displaystyle \frac{d}{dx} \operatorname{arccsc}(x) = -\frac{1}{x \sqrt{x^2-1}}\)

È interessante notare che, quando si calcola la derivata delle funzioni trigonometriche inverse, nessuna delle derivate trigonometriche inverse coinvolge funzioni trigonometriche o funzioni trigonometriche inverse.

Applicazioni della derivata di funzioni trigonometriche inverse

Le funzioni trigonometriche e le loro derivate, così come le funzioni trigonometriche inverse e le loro derivate fanno parte dell'inventario delle funzioni e delle operazioni di base, utilizzate come elementi costitutivi, per creare funzioni più complicate.

Sebbene le funzioni trigonometriche appariranno più spesso nelle applicazioni rispetto alle funzioni trigonometriche inverse, anche queste ultime hanno un posto chiaro nel calcolo, specialmente quando si differenziano e si utilizza il metodo di decomposizione delle frazioni parziali.

Suggerimenti e trucchi

Non dimenticare che le derivate delle funzioni trigonometriche inverse possono essere estremamente utili, specialmente quando si integrano termini che hanno un denominatore quadratico.

Inoltre, è facile commettere errori quando si calcolano le derivate trigonometriche inverse per definizione, potresti sicuramente trarre vantaggio dall'utilizzo di a calcolatore derivato che mostrerà i passaggi o che puoi usare per controllare il tuo lavoro.

Esempio: derivati trigonometrici inversi

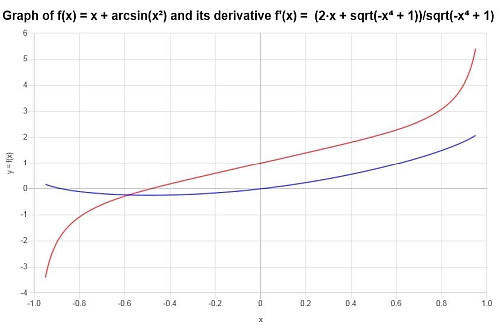
Calcola la derivata di: \(f(x) = x + \arcsin(x^2)\)

Soluzione: Per questo primo esempio, analizzeremo \(\displaystyle f(x)=x+\arcsin\left(x^2\right)\). Questa funzione comporta una funzione trigonometrica inversa, composta da un'altra funzione. Calcoliamo la sua derivata:

Risposta : Possiamo concludere che la derivata della funzione è:

\[f'(x) = \frac{2x+\sqrt{1-x^4}}{\sqrt{1-x^4}}\]

Possiamo vedere sia la funzione che la sua derivata nel grafico seguente:

Esempio: derivate trigonometriche più inverse

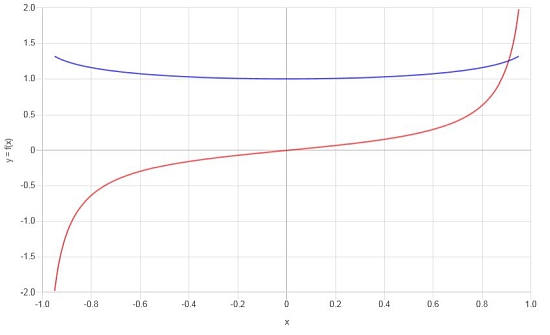
Considera la seguente funzione: \(f(x) = \frac{\arcsin(x)}{x}\), calcola la sua derivata.

Soluzione: Ora, per il secondo esempio, abbiamo la funzione \(\displaystyle f(x)=\frac{\arcsin\left(x\right)}{x}\).

Conclusione Finale : La derivata che stiamo cercando è:

\[f'(x) = \frac{-\left(\sqrt{1-x^2}\cdot\arcsin\left(x\right)-x\right)}{\sqrt{1-x^2}\cdot x^2}\]

Graficamente abbiamo:

Esempio di derivati trigonometrici inversi

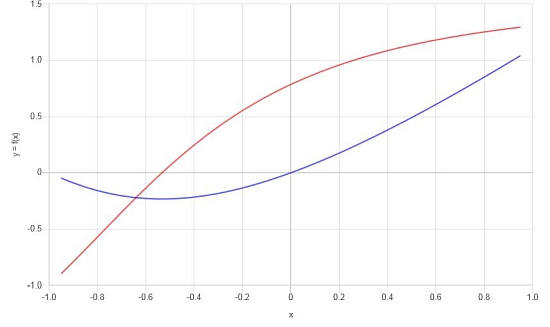
Calcola la derivata di: \(f(x) = x \arctan(x+1)\)

Soluzione: Ora, per questo ultimo esempio, lavoreremo con la funzione \(\displaystyle f(x)=x\arctan\left(x+1\right)\), che contiene una funzione inversa.

Conclusione : Dopo aver semplificato, la derivata è:

\[f'(x) = \frac{x^2\arctan\left(x+1\right)+2x\arctan\left(x+1\right)+x+2\arctan\left(x+1\right)}{x^2+2x+2}\]

Sulla base dei risultati trovati, possiamo costruire il seguente grafico per f e f':

Altri calcolatori di calcolo

Quando si usa derivati trigonometrici , abbiamo affermato che si trattava di elementi costitutivi cruciali per l'applicazione di base Regole derivate .

Le derivate per le funzioni trigonometriche inverse possono essere derivate semplicemente da Derivati delle derivate trigonometriche di base, ed è per questo che le consideriamo anche all'interno del gruppo delle derivate di base da imparare o addirittura memorizzare.