Calcolatrice di equazioni radicali
Istruzioni: Utilizzate questa calcolatrice di equazioni radicali per risolvere qualsiasi equazione che coinvolga i radicali da voi forniti, mostrando tutte le fasi del processo. Digitare l'equazione radicale che si desidera risolvere nella casella sottostante.
Risoluzione di equazioni radicali
Questo risolutore di equazioni radicali consente di gestire le equazioni radicali fornite dall'utente, manipolandole algebricamente e mostrando tutte le fasi del processo.
Questo risolutore accetta qualsiasi equazione valida che coinvolga le radici, ad esempio qualcosa di molto semplice come "sqrt(x) = 1", o qualcosa che può essere molto più difficile da risolvere come "sqrt(x+3) = x^2 - 1".
Una volta fornita un'equazione radicale valida, il gioco è praticamente fatto e non resta che cliccare su "Risolvi" per ottenere tutti i passaggi del processo mostrato.
La soluzione dell'equazione radicale forte si basa sull'efficace manipolazione algebrica dell'espressione per eliminare la parte radicale.

Che cos'è l'equazione radicale
Un'equazione radicale, in termini estremamente semplici, è un tipo di equazione di equazione matematica in cui l'incognita (tipicamente x) è all'interno di un radicale. Ad esempio
\[\displaystyle \sqrt x = x^2 \]è un'equazione radicale, a causa del termine \( \sqrt x\), ma l'equazione
\[\displaystyle 2 x = x^2 \]ad esempio, NON è un'equazione radicale, perché non è possibile inserire un radicale in nessun punto dell'equazione.
Come risolvere le equazioni radicali
Risolvere le equazioni radicali non è difficile se si seguono questi passaggi:
- Passo 1: Innanzitutto, assicuratevi di avere a che fare con un'equazione radicale. Un altro tipo di equazione sarà probabilmente risolto in modo diverso
- Passo 2: Semplificare e raggruppare i radicali il più possibile, avendo idealmente tutto concentrato in un'unica radicale
- Passaggio 3: Applicare una potenza (tipicamente una potenza di 2) per eliminare i radicali. Se si è agito correttamente e l'equazione è facilmente risolvibile, si ridurrà l'equazione originale a un'equazione di tipo Equazione polinomiale .
- Passaggio 4: Risolvere la funzione ausiliaria e verificare quale delle soluzioni ausiliarie (se presenti) è una soluzione dell'equazione originale
A volte, nonostante i raggruppamenti e le semplificazioni appropriate, non sarà possibile eliminare del tutto i radicali, oppure si otterrà un'equazione ancora più complicata.
Semplificazione di equazioni radicali
Come abbiamo detto in precedenza, il successo del calcolo di equazioni che coinvolgono radici dipende fortemente dalla capacità di semplificare i radicali . Ma a volte non è sufficiente, poiché la semplificazione di tutti i radicali non li farà scomparire. Il metodo più comune è quello di ridurre i radicali e poi applicare il quadrato (potenza di 2) per annullare il radicale.
Ma la quadratura per eliminare il radicale è una doppia spada, perché con la quadratura potrebbe scomparire qualsiasi segno rilevante. Per questo motivo, quando si "elimina" il radicale e si trovano le soluzioni di un'equazione ausiliaria, è necessario verificare che le soluzioni ausiliarie siano anche soluzioni dell'equazione originale. Spesso non lo sono.

Un altro modo per vedere il processo di eliminazione del radicale è quello di utilizzare una sostituzione adeguata. Ad esempio, per l'equazione radicale
\[\displaystyle \sqrt x = x \]si può impostare \(u = \sqrt x\), quindi \(u^2 = (\sqrt x)^2 = x\), in modo che l'equazione originale si trasformi nella seguente equazione ausiliaria:
\[\displaystyle \sqrt x = x \Rightarrow u = u^2\]che è un'equazione polinomiale che possiamo risolvere. Quindi, utilizzando una sostituzione si passa da un'equazione che non sappiamo come risolvere a risolvere un'equazione polinomiale che sappiamo chi deve risolvere.
Perché ci interessano le equazioni radicali?
Le equazioni radicali sono comuni in Algebra e in Calcolo, in quanto sono alla base della modellazione di molti fenomeni diversi.
Le funzioni radicali sono interessanti per le loro proprietà e per il tipo di crescita lenta quando x si avvicina all'infinito.

Esempio: risoluzione di equazioni con radicali
Risolvere il seguente problema: \(\sqrt{x} = 2x\)
Soluzione:
Ci viene fornita la seguente equazione. Dobbiamo risolvere questa equazione che ha una sola variabile, che è \(x\), quindi l'obiettivo è risolvere per \(x\):
\[\sqrt{x}=x^2\]Osserva che il grado del polinomio dato è \(\displaystyle deg(p) = 4\), il suo coefficiente principale è \(\displaystyle a_{4} = -1\) e il suo coefficiente costante è \(\displaystyle a_0 = 0\).
Tentativo di radici razionali
Candidati Radici Razionali : Dato che il primo termine con coefficiente non nullo in \(p(x)\) è \(x\), possiamo estrarre questo termine per ottenere
\[\displaystyle p(x) = -x^4+x = x \left(-x^3+1 \right) \]ma il termine tra parentesi ha grado superiore a 2, quindi non esiste una formula elementare per fattorizzarlo. Dobbiamo verificare le possibili radici razionali.
Il compito successivo è quello di trovare i numeri interi che dividono il coefficiente principale \(a_{3}\) e il coefficiente costante \(a_0\), che verranno utilizzati per costruire i nostri candidati zeri dell'equazione polinomiale.
i divisori di \(a_{3} = -1\) sono: \(\pm 1\).
i divisori di \(a_0 = 1\) sono: \(\pm 1\).
Pertanto, dividendo ogni divisore del coefficiente costante \(a_0 = 1\) per ogni divisore del coefficiente principale \(a_{3} = -1\), troviamo il seguente elenco di candidati ad essere radici:
\[\pm \frac{ 1}{ 1}\]Ora, tutti i candidati devono essere testati per vedere se sono una soluzione. Quanto segue si ottiene testando ogni candidato:
\[\begin{array}{ccccclcc} x & = & \displaystyle -1 &:& & \displaystyle -\left(-1^3\right)+1 & = & \displaystyle 2 \ne 0 \\\\ x & = & \displaystyle 1 &:& & \displaystyle -1^3+1 & = & \displaystyle 0 \\\\ \end{array}\]Divisione Polinomiale : Poiché non abbiamo abbastanza radici tra i candidati razionali, divideremo \(\displaystyle -x^3+1\) per il prodotto dei fattori derivati dalle radici razionali, che è \(\displaystyle \left(x-1\right) \).
Passo 1: Il termine iniziale del dividendo \(\displaystyle p(x) = -x^3+1\) è \(\displaystyle -x^3\), mentre il termine iniziale del divisore \(\displaystyle s(x) = x-1\) è uguale a \(\displaystyle x\).
Quindi, il termine che dobbiamo moltiplicare per \(x\) per arrivare al termine iniziale del dividendo è \(\displaystyle \frac{ -x^3}{ x} = -x^2\), quindi aggiungiamo questo termine al quoziente. Inoltre, moltiplichiamo questo termine per il divisore per ottenere \(\displaystyle -x^2 \cdot \left(x-1\right) = -x^3+x^2\), che dobbiamo sottrarre al dividendo:
\[\def\arraystretch{1.5}\begin{array}{rcccc} &\displaystyle -x^2 & \displaystyle & \displaystyle &\\[0.3em] \hline x-1\,) & \displaystyle -x^3 & \displaystyle & \displaystyle & \displaystyle +1\\[0.3em] \displaystyle &\displaystyle x^3 & \displaystyle -x^2 & \displaystyle & \displaystyle \\[0.3em] \hline \displaystyle &\displaystyle & \displaystyle -x^2 & \displaystyle & \displaystyle +1\\[0.3em] \end{array}\]Passo 2: Ora, il termine iniziale del resto corrente \(\displaystyle -x^2+1\) è \(\displaystyle -x^2\) e sappiamo che il termine iniziale del divisore è \(\displaystyle x\).
Quindi, il termine che dobbiamo moltiplicare per \(x\) per arrivare al termine iniziale del resto attuale è \(\displaystyle \frac{ -x^2}{ x} = -x\), quindi aggiungiamo questo termine al quoziente. Inoltre, moltiplichiamo questo termine per il divisore per ottenere \(\displaystyle -x \cdot \left(x-1\right) = -x^2+x\), che dobbiamo sottrarre al resto attuale:
\[\def\arraystretch{1.5}\begin{array}{rcccc} &\displaystyle -x^2 & \displaystyle -x & \displaystyle &\\[0.3em] \hline x-1\,) & \displaystyle -x^3 & \displaystyle & \displaystyle & \displaystyle +1\\[0.3em] \displaystyle &\displaystyle x^3 & \displaystyle -x^2 & \displaystyle & \displaystyle \\[0.3em] \hline \displaystyle &\displaystyle & \displaystyle -x^2 & \displaystyle & \displaystyle +1\\[0.3em] \displaystyle &\displaystyle & \displaystyle x^2 & \displaystyle -x & \displaystyle \\[0.3em] \hline \displaystyle &\displaystyle & \displaystyle & \displaystyle -x & \displaystyle +1\\[0.3em] \end{array}\]Passaggio 3: Ora, il termine iniziale del resto corrente \(\displaystyle -x+1\) è \(\displaystyle -x\) e sappiamo che il termine iniziale del divisore è \(\displaystyle x\).
Quindi, il termine che dobbiamo moltiplicare per \(x\) per arrivare al termine iniziale del resto attuale è \(\displaystyle \frac{ -x}{ x} = -1\), quindi aggiungiamo questo termine al quoziente. Inoltre, moltiplichiamo questo termine per il divisore per ottenere \(\displaystyle -1 \cdot \left(x-1\right) = -x+1\), che dobbiamo sottrarre al resto attuale:
\[\def\arraystretch{1.5}\begin{array}{rcccc} &\displaystyle -x^2 & \displaystyle -x & \displaystyle -1&\\[0.3em] \hline x-1\,) & \displaystyle -x^3 & \displaystyle & \displaystyle & \displaystyle +1\\[0.3em] \displaystyle &\displaystyle x^3 & \displaystyle -x^2 & \displaystyle & \displaystyle \\[0.3em] \hline \displaystyle &\displaystyle & \displaystyle -x^2 & \displaystyle & \displaystyle +1\\[0.3em] \displaystyle &\displaystyle & \displaystyle x^2 & \displaystyle -x & \displaystyle \\[0.3em] \hline \displaystyle &\displaystyle & \displaystyle & \displaystyle -x & \displaystyle +1\\[0.3em] \displaystyle &\displaystyle & \displaystyle & \displaystyle x & \displaystyle -1\\[0.3em] \hline \displaystyle & & & & 0\\[0.3em] \end{array}\]Pertanto, il quoziente è \(\displaystyle q(x) = -x^2-x-1\) e il resto è \(\displaystyle r(x) = 0\).
Quindi dopo aver diviso, siamo avanzati nella fattorizzazione con
\[\displaystyle p(x) = -x^4+x = - x \left(x-1\right) \left(-x^2-x-1\right)\]Ma ora, poiché il quoziente trovato \(\displaystyle -x^2-x-1\) è quadratico, possiamo trovare le sue radici per vedere se possiamo fattorizzarlo sul campo reale.
Dobbiamo risolvere la seguente equazione quadratica \(\displaystyle -x^2-x-1=0\).
Usando la formula quadratica
Per un'equazione quadratica della forma \(a x^2 + bx + c = 0\), le radici vengono calcolate utilizzando la seguente formula:
\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a}\]In questo caso, abbiamo che l'equazione da risolvere è \(\displaystyle -x^2-x-1 = 0\), il che implica che i coefficienti corrispondenti sono:
\[a = -1\] \[b = -1\] \[c = -1\]Innanzitutto, calcoleremo il discriminante per valutare la natura delle radici. La discriminante è calcolata come:
Poiché in questo caso il discriminante è \(\Delta = \displaystyle -3 < 0\), che è negativo, sappiamo che l'equazione data ha due diverse radici complesse coniugate.
Ora, inserendo questi valori nella formula per le radici otteniamo:
\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a} = \displaystyle \frac{1 \pm \sqrt{\left(-1\right)^2-4\left(-1\right)\left(-1\right)}}{2\cdot -1} = \displaystyle \frac{1 \pm \sqrt{-3}}{-2}\]allora, troviamo che:
\[\displaystyle {x}_1 = \frac{1 - i \sqrt{3}}{-2} = -\frac{1}{2}+\frac{1}{2}\sqrt{3}i\] \[\displaystyle {x}_2 = \frac{1 + i \sqrt{3}}{-2} = -\frac{1}{2}-\frac{1}{2}\sqrt{3}i\]Quindi, dopo aver trovato le radici dell'ultima parte quadratica, troviamo due radici complesse, quindi non possiamo fattorizzare il termine \(-x^2-x-1\) nel campo reale, quindi terminiamo il processo con \(\displaystyle p(x) = -x^4+x = - x \left(x-1\right) \left(-x^2-x-1\right)\).
Conclusione : Pertanto, la fattorizzazione finale che otteniamo è:
\[\displaystyle p(x) = -x^4+x = - x\left(x-1\right)\left(-x^2-x-1\right)\]Le radici trovate con il processo di fattorizzazione sono \(0\), \(1\), \(-\frac{1}{2}+\frac{1}{2}\sqrt{3}i\) e \(-\frac{1}{2}-\frac{1}{2}\sqrt{3}i\) .
Pertanto, la soluzione di \(x\) per l'equazione polinomiale data porta alle soluzioni \(x = \, \)\(0\), \(1\), \(-\frac{1}{2}+\frac{1}{2}\sqrt{3}i\), \(-\frac{1}{2}-\frac{1}{2}\sqrt{3}i\), utilizzando i metodi di fattorizzazione.
Controllo delle soluzioni ausiliarie
La verifica di queste soluzioni dall'equazione polinomiale ausiliaria mostra che non tutte le soluzioni candidate sono in realtà una soluzione dell'equazione originale. Le uniche soluzioni effettive dell'equazione originale sono:
\[x_1=0 \]\[x_2=1 \]
Pertanto, la soluzione di \(x\) per l'equazione data porta alla soluzione \(x=0,\,\,x=1\).
Graficamente
Di seguito è riportata la rappresentazione grafica delle soluzioni ottenute:
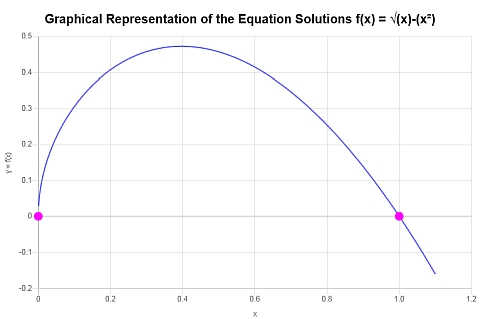
che conclude il calcolo.
Altri utili risolutori di equazioni
Quando si risolvono le equazioni radicali, a differenza del caso in cui è necessario Risolvi equazioni lineari o quando è necessario risolvere un'equazione quadratica rientra nella categoria di quelle equazioni che richiedono un'abile manipolazione algebrica per risolvere la x.
In altre parole, non si può dire "fai così e funzionerà sempre". Il tipo di manipolazione dipende dalla struttura dell'equazione e può variare notevolmente da caso a caso.
espressioni semplificative è sempre una buona pratica, perché si riducono i termini che possono ingombrare la struttura complessiva dell'equazione.



