Résolveur d'équations quadratiques

Cette calculatrice vous permettra calculer une équation quadratique que vous fournissez, montrant toutes les étapes. Tout ce que vous devez faire est de fournir une équation quadratique valide.

Il peut s'agir de quelque chose qui est déjà simplifié et prêt à être résolu comme x^2 + 3x + 5 = 0, vous pouvez fournir quelque chose qui n'est pas facilement simplifié comme 3x^2 - 4x + 5/3 = x^2 +1/3x -1, par exemple .

Une fois que vous avez fourni une équation quadratique valide, tout ce que vous avez à faire est de cliquer sur "Calculer", et toutes les étapes du processus de calcul de l'équation quadratique vous seront présentées racines de l'équation quadratique qui est fourni.

Habituellement, vous utiliserez la formule quadratique pour calculer des équations quadratiques, mais ce n'est pas la seule façon, comme nous le verrons dans les sections suivantes.

Comment calculer une équation quadratique ?

Il existe plusieurs stratégies pour résoudre les équations quadratiques. La plus couramment utilisée est l'utilisation de la fonction formule quadratique . De plus, vous pouvez résoudre par compléter des carrés ou vous pouvez résoudre par factorisation quadratique .

Quelles sont les étapes du calcul des équations quadratiques à l'aide de la formule quadratique ?

• Étape 1 : Identifiez l'équation quadratique que vous voulez calculer
• Étape 2 : Assurez-vous que l'équation est entièrement simplifiée, sinon continuez la simplification, jusqu'à ce que vous ayez une équation de la forme ax² + bx + c = 0
• Étape 3 : Une fois l'équation réduite à sa forme simplifiée, vous pouvez utiliser la formule quadratique : \(x = \displaystyle \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\)

Il est possible que l'utilisation de la formule d'équation quadratique soit le moyen le plus pratique de trouver les racines d'une équation quadratique, mais il existe d'autres raisons pour lesquelles vous utiliseriez d'autres méthodes.

Comment résoudre une équation quadratique en complétant les carrés ?

La deuxième façon la plus courante de résoudre une équation quadratique est d'utiliser la technique du compléter des carrés . Il n'y a pas vraiment de formule pour compléter les carrés (bien que techniquement il y en ait une, basée sur les solutions de l'équation quadratique), et c'est plutôt un processus.

Quelles sont les étapes pour compléter les carrés

• Étape 1 : Identifiez l'équation quadratique que vous voulez résoudre
• Étape 2 : Vous devez vous assurer que l'équation est entièrement simplifiée et que vous avez une équation de la forme ax² + bx + c = 0
• Étape 3 : Ajouter et soustraire un terme approprié (dans ce cas, (b/(2a))² pour forcer les termes du carré d'un binôme

L'idée du pour forcer l'apparition d'un terme de la forme (x + "quelque chose)², qui est le but ultime de la complétion des carrés.

Pourquoi utiliseriez-vous des équations quadratiques ?

Les équations quadratiques apparaissent constamment dans les applications d'algèbre sont des problèmes de mots. La résolution d'équations quadratiques est une des compétences de base que vous devez acquérir.

Ensuite, dans des domaines comme le calcul, lors du calcul de problèmes de maximisation et de minimisation, vous devrez avoir une bonne connaissance de tous les types d'équations quadratiques.

Exemple : résolution d'une équation quadratique

Résolvez l'équation quadratique suivante en utilisant la formule \(4x^2 + \frac{4}{3}x + 2 = 0\)

Solution: Nous devons résoudre l'équation quadratique suivante \(\displaystyle 4x^2+\frac{4}{3}x+2=0\).

Pour une équation quadratique de la forme \(a x^2 + bx + c = 0\), les racines sont calculées à l'aide de la formule suivante :

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a}\]

Dans ce cas, nous avons que l'équation que nous devons résoudre est \(\displaystyle 4x^2+\frac{4}{3}x+2 = 0\), ce qui implique que les coefficients correspondants sont :

\[a = 4\] \[b = \frac{4}{3}\] \[c = 2\]

Tout d'abord, nous allons calculer le discriminant pour évaluer la nature des racines. Le discriminant est calculé comme suit :

\[\Delta = b^2 - 4ac = \displaystyle \left( \frac{4}{3}\right)^2 - 4 \cdot \left(4\right)\cdot \left(2\right) = -\frac{272}{9}\]

Puisque dans ce cas nous obtenons le discriminant est \(\Delta = \displaystyle -\frac{272}{9} < 0\), qui est négatif, nous savons que l'équation donnée a deux racines complexes conjuguées différentes.

En introduisant ces valeurs dans la formule des racines, nous obtenons :

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a} = \displaystyle \frac{-\frac{4}{3} \pm \sqrt{\left(\frac{4}{3}\right)^2-4\left(4\right)\left(2\right)}}{2\cdot 4} = \displaystyle \frac{-\frac{4}{3} \pm \sqrt{-\frac{272}{9}}}{8}\]

donc, nous trouvons que :

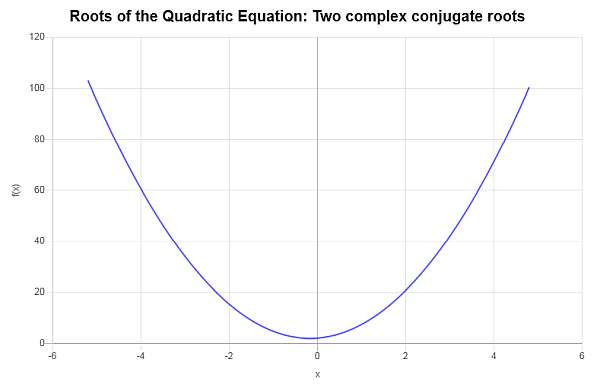
\[\displaystyle x_1 = \frac{-\frac{4}{3} - i \sqrt{\frac{272}{9}}}{8} = -\frac{1}{6} - \frac{1}{6}\sqrt{17} i\] \[\displaystyle x_2 = \frac{-\frac{4}{3} + i \sqrt{\frac{272}{9}}}{8} = -\frac{1}{6} + \frac{1}{6}\sqrt{17} i\]

Par conséquent, l'équation donnée \(\displaystyle 4x^2+\frac{4}{3}x+2=0\) a deux racines complexes conjuguées différentes, qui sont \(x_1 = \displaystyle -\frac{1}{6} - \frac{1}{6}\sqrt{17} i\) et \(x_2 = \displaystyle -\frac{1}{6} + \frac{1}{6}\sqrt{17} i\).

Graphiquement :

Exemple : racine d'une équation quadratique

Trouvez les racines de l'équation quadratique suivante en complétant les carrés \(2x^2 + \frac{1}{3}x + \frac{1}{72} = 0\)

Solution: Dans ce cas, nous avons que l'équation que nous devons résoudre est \(\displaystyle 2x^2+\frac{1}{3}x+\frac{1}{72} = 0\), ce qui implique que les coefficients correspondants sont :

\[a = 2\] \[b = \frac{1}{3}\] \[c = \frac{1}{72}\]

La discrimination est calculée comme suit :

\[\Delta = b^2 - 4ac = \displaystyle \left( \frac{1}{3}\right)^2 - 4 \cdot \left(2\right)\cdot \left(\frac{1}{72}\right) = 0\]

Puisque dans ce cas on obtient le discriminant est \(\Delta = \displaystyle 0 = 0\), qui est nul, on sait que l'équation n'a qu'une seule racine réelle.

En introduisant ces valeurs dans la formule des racines, nous obtenons :

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a} = \displaystyle \frac{-\frac{1}{3} \pm \sqrt{\left(\frac{1}{3}\right)^2-4\left(2\right)\left(\frac{1}{72}\right)}}{2\cdot 2} = \displaystyle \frac{-\frac{1}{3} \pm \sqrt{0}}{4}\]

donc, nous trouvons que :

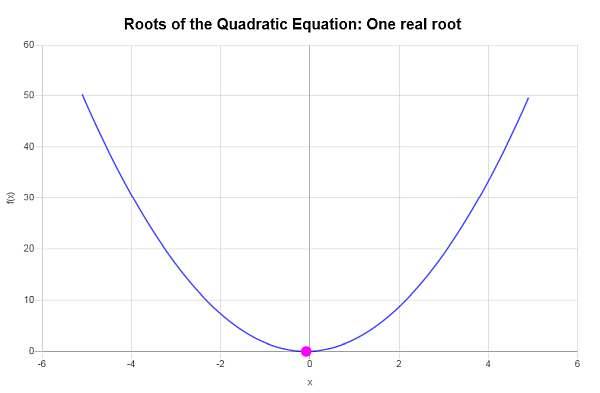
\[x = \displaystyle \frac{-\frac{1}{3}}{4} = \displaystyle -\frac{1}{12}\]

Par conséquent, l'équation donnée \(\displaystyle 2x^2+\frac{1}{3}x+\frac{1}{72}=0\) n'a qu'une seule racine réelle, qui est \(x = \displaystyle -\frac{1}{12}\).

Graphiquement :

Exemple : calcul des racines d'une équation

Résolvez le problème suivant : \(3x^2 + \frac{2}{3}x - \frac{4}{3} = 0\)

Solution: Pour cet exemple, l'équation que nous devons résoudre est \(\displaystyle 3x^2+\frac{2}{3}x-\frac{4}{3} = 0\), alors les coefficients correspondants sont :

\[a = 3\] \[b = \frac{2}{3}\] \[c = -\frac{4}{3}\]

Dans ce cas, la discrimination est calculée comme suit :

\[\Delta = b^2 - 4ac = \displaystyle \left( \frac{2}{3}\right)^2 - 4 \cdot \left(3\right)\cdot \left(-\frac{4}{3}\right) = \frac{148}{9}\]

Comme le discriminant est \(\Delta = \displaystyle \frac{148}{9} > 0\), qui est positif, nous savons que l'équation aura deux racines réelles différentes.

En introduisant ces valeurs dans la formule des racines, nous obtenons :

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a} = \displaystyle \frac{-\frac{2}{3} \pm \sqrt{\left(\frac{2}{3}\right)^2-4\left(3\right)\left(-\frac{4}{3}\right)}}{2\cdot 3} = \displaystyle \frac{-\frac{2}{3} \pm \sqrt{\frac{148}{9}}}{6}\]

donc, nous trouvons que :

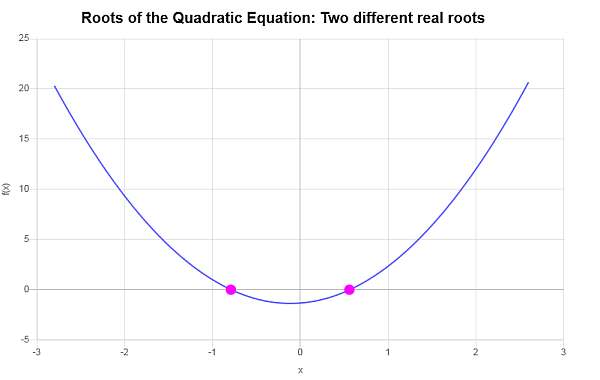
\[ x_1 = -\frac{\frac{2}{3}}{6}-\frac{1}{6}\sqrt{\frac{148}{9}}=-\frac{1}{9}\sqrt{37}-\frac{1}{9} \] \[x_2 = -\frac{\frac{2}{3}}{6}+\frac{1}{6}\sqrt{\frac{148}{9}}=\frac{1}{9}\sqrt{37}-\frac{1}{9}\]

Par conséquent, l'équation donnée \(\displaystyle 3x^2+\frac{2}{3}x-\frac{4}{3}=0\) a deux racines réelles différentes, qui sont \(x_1 = \displaystyle -\frac{1}{9}\sqrt{37}-\frac{1}{9}\) et \(x_2 = \displaystyle \frac{1}{9}\sqrt{37}-\frac{1}{9}\).

Graphiquement :

Autres calculatrices quadratiques utiles

Comme nous l'avons vu dans ce tutoriel, compléter des carrés joue un rôle fondamental dans le calcul des équations quadratiques. Vous pouvez également utiliser cette calculateur de discriminants d'évaluer la nature des racines (deux racines réelles, une racine réelle ou deux racines complexes) sans résoudre l'équation.

Vous pouvez également utiliser ce Calculateur de sommets pour trouver les coordonnées du sommet d'une équation quadratique, et trouver l'axe de symétrie d'une parabole . Vous pouvez également explorer cette factorisation quadratique pour explorer une autre façon de calculer les équations quadratiques.