Comment utiliser cette calculatrice de théorème de Pythagore

1. Vous avez trois cases où vous pouvez saisir des données
2. Les formes représentent les côtés a et b, et l'hypoténuse c
3. Veuillez saisir les valeurs de DEUX de ces cases
4. Par exemple, si vous savez que les côtés sont a = 3 et b = 4, alors vous tapez 3 dans la première forme et 4 dans la deuxième case
5. Ou, par exemple, si vous savez que l'hypoténuse est c = 10/3 et que le côté a est 5, alors vous tapez 5 dans la première forme, et 10/3 dans la troisième case et laissez la deuxième case vide

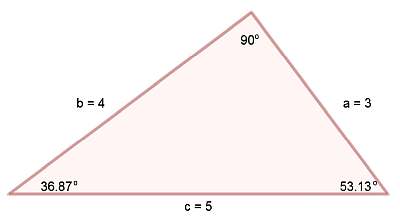
Formule du théorème de Pythagore

La formule de base de Pythagore est

\[\large a^2 + b^2 = c^2\]

et cette formule vous dit comment trouver "c" si vous connaissez "a" et "b".

Mais aussi, vous pouvez trouver "a" si vous connaissez "c" et "b", et vous pouvez résoudre "b" si vous connaissez "c" et "a".

Comment résoudre des triangles rectangles

Cette calculatrice de théorème de Pythagore vous montrera toutes les étapes du calcul de la formule du théorème de Pythagore.

Ce n'est pas seulement une calculatrice d'hypoténuse, car vous pouvez également fournir un côté et l'hypoténuse, et la calculatrice vous montrera toutes les étapes pour obtenir l'autre côté.

L'application la plus typique est celle où vous avez deux côtés dans un triangle rectangle et vous voulez obtenir l'hypoténuse. Mais finalement, l'idée dans un triangle rectangle est que si vous avez deux côtés (en général), vous pouvez obtenir le troisième côté en utilisant une version de la formule de Pythagore.

Ainsi, avec deux informations, vous pouvez trouver la longueur du côté manquant.

S'agit-il uniquement d'une calculatrice de triangle rectangle

Oui c'est le cas. Cette calculatrice ne traite que des triangles rectangles. Si votre triangle n'est pas droit, vous pouvez utiliser ceci Calculatrice triangulaire SAS (où vous fournissez deux côtés et un angle, qui peut être n'importe quel angle, pas nécessairement 90 ^O .), cette Calculatrice triangulaire SSS (où vous connaissez les trois côtés et vous voulez trouver tous les angles).

Ou, vous pourriez ceci Calculatrice triangulaire AAS (où vous connaissez deux angles et le côté opposé).

Comment calculer le théorème de Pythagore ?

Étape 1: Tout d'abord, vous devez évaluer les informations dont vous disposez. As-tu les deux côtés a et b, et tu cherches l'hypothénuse c ? Ou connaissez-vous c et a, ou c et b ?

Étape 2: Si vous connaissez les deux côtés a et b, cette calculatrice d'hypoténuse obtiendra l'hypoténuse en utilisant la formule suivante

\[c = \sqrt{a^2 + b^2}\]

et c'est ainsi que vous trouvez l'hypoténuse.

Étape 3: Si vous connaissez un côté et l'hypoténuse, dites donc que vous connaissez a et c, maintenant la calculatrice obtiendra l'autre côté, b, en utilisant la formule suivante

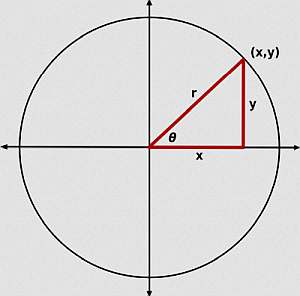
\[b = \sqrt{c^2 - b^2}\]

L'angle de la calculatrice du théorème de Pythagore

Cette calculatrice nécessite que l'un des angles soit de 90 ^O pour que la formule de Pythagore soit valide.

Pouvez-vous utiliser Pythagore pour les angles ? Non, notez que cette calculatrice de Pythagore ne traite que des côtés et qu'elle ne calcule pas les angles.

Si vous voulez résoudre complètement un triangle (résoudre un triangle signifie trouver des côtés et des angles), vous pouvez les utiliser : Calculatrice triangulaire SAS , Calculatrice triangulaire SSS et Calculatrice triangulaire AAS .

Exemple de calcul d'un triangle rectangle

Question: Supposons que les côtés d'un triangle rectangle sont a = 3 et b = 3. Utilisez le théorème de Pythagore pour calculer l'hypothénuse c.

Solution: Nous avons reçu deux côtés, \(a =\displaystyle3\) et \(b = \displaystyle 6\). Nous devons utiliser la formule de Pythagore pour calculer l'hypothénuse \(c\).

Sur la base de ces informations, la formule de Pythagore suivante doit être utilisée :

\[c = \displaystyle\sqrt{a^2 + b^2}\]

Alors maintenant, en branchant les valeurs dont nous disposons, on obtient ce qui suit :

\[c = \displaystyle\sqrt{a^2 + b^2} = \displaystyle\sqrt{3^2 + 6^2} = \displaystyle\sqrt{9 + 36} = \displaystyle\sqrt{45} = 3\sqrt{5}\]

Par conséquent, et en résumé, nous avons trouvé que \(a = 3\), \(b = 6\) et \(c = 3\sqrt{5}\).