Algèbre Tutoriels

Le théorème binomial

Le théorème binomial est l'un des théorèmes les plus célèbres de l'algèbre, et il a une multitude d'applications dans les domaines de l'algèbre, des probabilités et des statistiques. Il énonce une formule agréable et concise pour le n ^e puissance de la somme de deux valeurs: \((a+b)^n\)

J'ai été présenté pour la première fois de manière informelle par Sir Isaac Newton en 1665.

De nombreux autres mathématiciens notables ont abordé le théorème binomial après Newton. C'était un problème très attrayant aux 17e et 18e siècles.

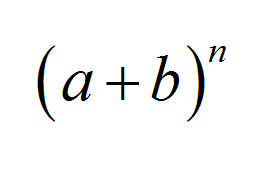
La formule de l'expansion binomiale

Ce qui est entier dans le théorème binomial, c'est qu'il fournit une formule très élégante et concise. Avant d'entrer dans la formule, faisons quelques calculs. Par exemple, pour \(n = 2\), nous obtenons:

\[\large (a+b)^2 = (a+b) \times (a+b) = a(a+b) + b(a+b) = a^2 + ba + ab + b^2 \] \[\large = a^2 + 2ab + b^2 \]

Essayons maintenant avec \(n = 3\):

\[\large (a+b)^3 = (a+b)^2 \times (a+b) = (a^2 + 2ab+b^2)(a+b) \] \[\large = a^3 + 2a^2b + ab^2 + a^2b + 2ab^2 + b^3 \] \[\large = a^3 + 3a^2b + 3ab^2 + b^3\]

Enfin, soyons courageux et essayons-le avec \(n = 4\):

\[\large (a+b)^4 = (a+b)^3 \times (a+b) = (a^3 + 3a^2b + 3ab^2 + b^3)(a+b) \] \[\large = a^4 + 3a^3 b + 3a^2b^2 + ab^3 + a^3b + 3a^2b^2 + 3ab^3 + b^4 \] \[\large = a^4 + 4a^3b + 6 a^2 b^2 + 4a b^3 + b^4\]

Ok, c'était courageux, n'est-ce pas, hein ?? Voyez-vous des modèles là-bas. Je peux en voir. Par exemple, pour \(n = 2\), nous pourrions le simplifier à 3 termes. Pour \(n = 3\), nous pourrions le simplifier à 4 termes, et pour \(n = 4\), nous pourrions le simplifier à 5 termes. Donc en général, je m'attends à ce que pour la puissance générale de \(n\), nous ayons des termes \(n+1\)

Plus de modèles? Eh bien, il y a toujours un terme de la forme \(a^l b^m\), et nous pouvons voir que les puissances \(l\) diminuent, et les puissances \(m\) augmentent. Mais il y a aussi quelque chose d'intéressant: si vous vérifiez chaque terme, la somme des puissances est toujours \(n\). En effet, vous vérifierez que \(l + m = n\) pour tous ces termes.

Par exemple, pour \(n = 2\), vous avez le terme \(2 a b\). La puissance de \(a\) est 1, la puissance de \(b\) est 1, et la somme des puissances est \(1 + 1 = 2\). Ou par exemple, pour \(n = 4\) vous avez le terme \(6 a^2 b^2\), où la puissance de \(a\) est 2, et la puissance de \(b\) est 2, et la somme des puissances est \(2 + 2 = 4\)

Le théorème binomial général

Nous sommes maintenant prêts à donner l'expression générale du théorème binomial. Prêt? Nous avons:

\[\large (a+b)^n = a^n + {n \choose 1} a^{n-1} b + {n \choose 2} a^{n-2} b^2 + ... + {n \choose n-1} a b^{n-1} + b^n \]

où le terme \({n \choose i}\) se lit comme "n choisit i" ou aussi comme "coefficient combinatoire", et il est défini comme

\[\large \displaystyle {n \choose i}= \frac{n!}{i! \times (n-i)!}\]

Par exemple,

\[\large \displaystyle {5 \choose 2} = \frac{5!}{2! \times (5-2)!} = \frac{5!}{2! \times 3!} = \frac{120}{2 \times 6} = 10\]

Vous pouvez utiliser ceci calculateur de coefficient combinatoire pour en savoir plus et pratiquer en voyant toutes les étapes indiquées.

Le théorème binomial général utilisant une sommation

La somme ci-dessus qui définit le théorème binomial utilise la notation par extension, pour rendre les termes plus compréhensibles. Comme toujours en Math, nous essayons de rendre les choses plus compactes, et l'expression ci-dessus peut être résumée comme suit:

\[\large \displaystyle (a+b)^n = \sum_{i=0}^n {n \choose i} a^i b^{n-i} \]

Observez les pouvoirs des termes dans l'extension. Le terme général est \(a^i b^{n-i}\) (fois une constante). La somme des puissances est \(i + (n-i) = n\). Ainsi, la somme des puissances de TOUS les termes de l'extension doit être \(n\). N'est-ce pas joli ???

EXEMPLE 1

Le terme \(x^3 y^2\) (fois une constante) peut-il faire partie de l'expansion de \((x+y)^6\)? Pourquoi?

RÉPONDRE:

La réponse est non. Dans ce cas, \(n = 6\), et nous savons du théorème binomial que la somme des puissances des termes \(x^l y^m\) dans le développement doit être égale à \(n\). Dans ce cas, \(l + m = 3 + 2 = 5\), qui n'est pas la même chose que \(n = 6\). Par conséquent, le terme \(x^3 y^2\) (fois une constante) ne peut pas faire partie du développement de \((x+y)^6\).

EXEMPLE 2

Développez \((a-b)^3\) en utilisant le théorème binomial.

RÉPONDRE:

Attendre. Vous devez penser: "Vous venez de m'apprendre à développer \((a+b)^n\), mais maintenant vous me posez des questions sur \((a-b)^n\). Pourquoi êtes-vous si cruel". Attendez. Je ne te joue pas des tours.

Il y a toujours une astuce (n'oubliez pas cette ligne, elle apparaît beaucoup en Math).

Observez que \(a - b\) est identique à \(a + (-b)\).

Ahhhhhhh, donc le théorème binomial s'applique toujours. Donc alors:

\[\large (a-b)^3 = (a+(-b))^3 = a^3 + {3 \choose 1} a^2 (-b) + {3 \choose 2} a (-b)^2 + (-b)^3 \] \[\large \displaystyle = a^3 - \frac{3!}{1! \times 2!} a^2 b + \frac{3!}{2! \times 1!} a b^2 -b^3 \] \[\large \displaystyle = a^3 - \frac{6}{1 \times 2} a^2 b + \frac{6}{2 \times 1} a b^2 -b^3 \] \[\large = a^3 - 3 a^2 b + 3 a b^2 -b^3 \]

En savoir plus sur l'expansion binomiale

Le théorème binomial est si important qu'il est couvert dans presque tous les cours, y compris l'algèbre, le calcul, les probabilités et les statistiques.

Il existe des généralisations comme l'expansion binomiale négative, qui dépasse le cadre de ce didacticiel.

Le triangle de Pascal

Parfois, les étudiants sont bloqués lorsqu'ils doivent calculer les constantes (les coefficients combinatoires) qui entrent dans le développement binomial. Un moyen très simple de le faire est d'utiliser le triangle de Pascal.

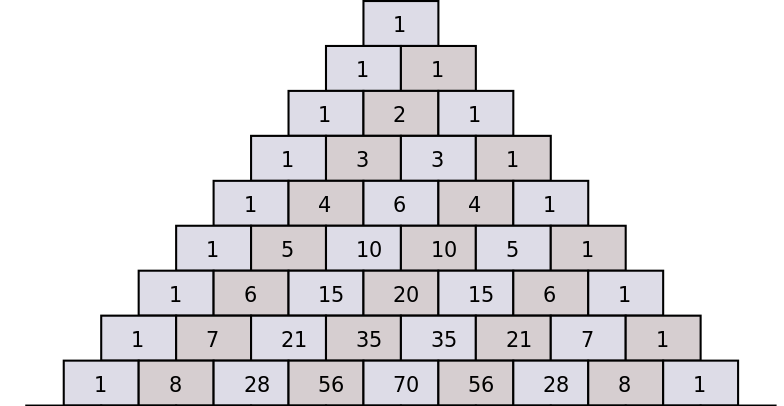
Le triangle de Pascal montre comment les coefficients binomiaux successifs peuvent être calculés à partir des coefficients de la valeur précédente de \(n\), en ajoutant les deux coefficients qui viennent immédiatement au-dessus.

Applications

L'expansion binomiale a de multiples applications en Algèbre et en Théorie des Probabilités. Par exemple, dans Probability, la distribution binomiale est basée sur le théorème binomial.

En effet, considérons un nombre \(0 \le p \le 1\). Ensuite, \(p + (1-p) = 1\) et nous pouvons utiliser le théorème binomial:

\[\large \displaystyle 1 = 1^n = (p + (1-p))^n = \sum_{i=0}^n {n \choose i} p^i (1-p)^{n-i} \]

ce qui signifie que

\[\large \displaystyle \sum_{i=0}^n {n \choose i} p^i (1-p)^{n-i} = 1 \]

Il s'avère que chacun des termes \({n \choose i} p^i (1-p)^{n-i}\) représente une probabilité. De plus, nous avons:

\[\large \Pr(X = i) = {n \choose i} p^i (1-p)^{n-i} = 1 \]

où \(X\) est le nombre de succès après \(n\) essais, lorsque la probabilité de succès de chaque essai est \(p\). La variable \(X\) est connue sous le nom de variable aléatoire binomiale.