Calculateur d'abscisse
Instructions: Utilisez cette calculatrice pour trouver l'ordonnée à l'origine d'une ligne, avec toutes les étapes indiquées. Pour ce faire, vous devez fournir la ligne pour laquelle vous avez besoin de l'abscisse à l'origine.
Veuillez fournir la ligne en fournissant soit : (1) la pente et l'ordonnée à l'origine, (2) une équation linéaire valide (ex : \(2x + \frac{1}{5}y = 3 + 2x\)), (3) la pente et un point par lequel la ligne passe , ou (4) deux points où passe la ligne. Veuillez sélectionner votre choix :
Comment utiliser cette calculatrice d'interception x avec étapes
Cette calculatrice vous permettra de calculer l'ordonnée à l'origine d'une ligne, et vous obtiendrez toutes les étapes indiquées.
L'abscisse à l'origine est le point où la ligne croise l'axe des x, si jamais cela se produit.
En général, il y a toujours une abscisse lorsque la pente est différente de zéro.
Lorsque la pente est nulle, il y aura une abscisse à l'origine uniquement si la ligne croise également l'origine. Les lignes verticales ont également une abscisse.
Comment trouver x intercepter avec des étapes avec cette calculatrice
Pour utiliser ce calculateur, il vous suffit de choisir l'une des quatre options proposées pour définir votre ligne. Souvent, vous fournirez la pente et l'ordonnée à l'origine, mais vous pouvez également noter la équation de la droite directement .
Si l'équation que vous avez fournie est valide, le solveur passera en revue les étapes nécessaires pour identifier l'abscisse à l'origine ou pour indiquer qu'aucune abscisse à l'origine n'a pu être trouvée
Pouvez-vous obtenir l'abscisse à l'origine d'une ligne sous forme standard ?
Oui! En fait, en utilisant le forme standard de la ligne est l'un des moyens les plus simples de calculer l'abscisse à l'origine.
Ainsi, une stratégie courante consiste à convertir d'abord l'équation de la ligne en forme standard, puis à résoudre pour \(x\) lorsque \(y=0\).
Pourquoi avons-nous besoin de l'abscisse à l'origine ?
L'abscisse à l'origine et Ordonnée à l'origine d'une ligne ont une grande utilité pour donner une intuition géométrique du comportement sur une ligne dans les axes de coordonnées \(X - Y\).

Exemple de calcul de l'abscisse donnée d'une droite
Vous connaissez la forme standard de la ligne \( \frac{3}{4} x + \frac{4}{5} y = 2\). Trouvez l'abscisse à l'origine de la droite.
Réponse:
On nous a fourni l'équation suivante :
\[\displaystyle 2x+y=y+5\]Alors, qui trouvez-vous x intercepter : En passant toutes les variables et leurs coefficients à gauche de l'équation, et en regroupant les constantes à droite, on obtient :
\[\displaystyle 2x+\left(1-1\right)y = 5\]et en simplifiant tous les termes à simplifier, on obtient que l'équation sous forme standard est
\[\displaystyle 2x=5\]Le terme \( y\) n'apparaît pas sur le côté gauche de l'équation, nous pouvons donc résoudre davantage pour \( x\), ce qui conduit à
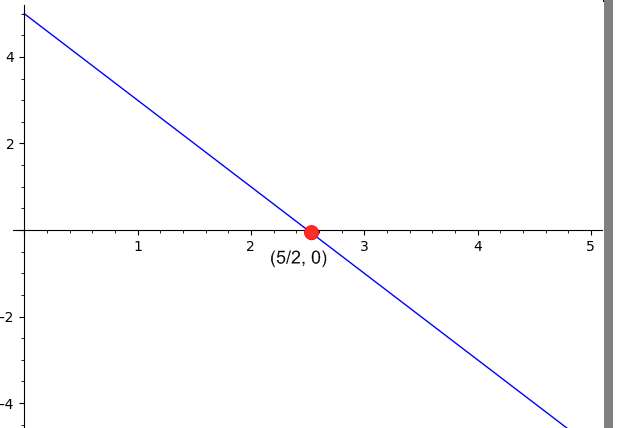
\[ 2 x = 5 \Rightarrow x=\frac{5}{2}\]Observez que sur la base de ce qui précède, cela correspond à une ligne verticale, qui traverse la valeur \(\displaystyle x=\frac{5}{2}\).
Conclusion : Sur la base des données fournies, nous concluons que la ligne croise l'axe des x à \(\displaystyle x = \frac{5}{2}\), par conséquent, le point d'intersection x correspondant est \(\displaystyle \left(\frac{5}{2}, 0\right)\).





