Un sistema de ecuaciones es simplemente un conjunto de dos o más ecuaciones simultáneas que es necesario resolver. Por lo general, tendrá el mismo número de ecuaciones e incógnitas (variables), pero no tiene por qué ser así.

Lo único que está claro es que para tener un sistema de ecuaciones es necesario tener DOS o MÁS ecuaciones simultáneas. Por ejemplo, el sistema siguiente

es un sistema de ecuaciones, con dos ecuaciones y dos incógnitas (\(x\) y \(y\)). O, por ejemplo, el siguiente sistema:

es un sistema de ecuaciones, con dos ecuaciones y tres incógnitas (\(x\), \(y\) y \(z\)).

El primer ejemplo es un ejemplo de un sistema de ecuaciones lineales.

El segundo ejemplo es un ejemplo de un sistema de ecuaciones no lineales. ¿Por qué? Lo adivinaste: el término \(z^2\) en la primera ecuación la hace no lineal.

En términos generales, la estrategia utilizada para resolver un sistema de ecuaciones depende de si es lineal o no. Para sistemas lineales de ecuaciones, existen métodos sistemáticos para resolverlos, como Regla de Cramer . Para los sistemas de ecuaciones no lineales, no hay una estrategia fija y tenemos que ir caso por caso.

Número de soluciones de un sistema de ecuaciones

¿Cuántas soluciones tiene un sistema de ecuaciones, si es que tiene alguna? Una respuesta general a esta pregunta solo se puede dar en el caso de sistemas de ecuaciones lineales, basada en la relación entre el número de ecuaciones y el número de incógnitas.

Por lo general, en un sistema de ecuaciones lineales donde el número de ecuaciones es igual o mayor que el número de incógnitas, podría haber una solución única, ninguna solución o infinitas soluciones.

Cuando el número de ecuaciones es menor que el número de incógnitas, podría haber un número infinito de soluciones o ninguna solución, pero no podría haber una solución única.

¿Cómo encuentras un sistema de ecuaciones?

Esta pregunta está relacionada con cómo se llega a un sistema de ecuaciones. Hay varios contextos. Por ejemplo, puede estar lidiando con un problema verbal, en el que está produciendo tres tipos diferentes de alimentos y tiene varios tipos de restricciones sobre esos alimentos en términos de costo, calorías, etc. Cada una de esas restricciones probablemente puede representado como una ecuación.

Existen innumerables aplicaciones en las que diferentes restricciones conducen a ecuaciones lineales que deben resolverse simultáneamente, convirtiendo el problema en un sistema de ecuaciones.

EJEMPLO 1

Ejemplo de sistema de ecuaciones: ¿Es el siguiente sistema de ecuaciones lineal o no lineal?

RESPONDER:

Primero que nada, lo anterior es un sistema de ecuaciones, con tres ecuaciones y tres incógnitas (\(x\), \(y\) y \(z\)). Las dos primeras ecuaciones son lineales si la última ecuación no es lineal, debido al término \(\sin(z)\). Para tener una ecuación lineal, necesitamos que las incógnitas solo se multipliquen por una constante.

Entonces, el sistema de ecuaciones anterior no es lineal, incluso si las dos primeras ecuaciones son lineales, la tercera no lo es. Para un sistema, es suficiente tener una ecuación para que no sea lineal para que todo el sistema sea no lineal.

EJEMPLO 2

Suponga que produce tres tipos de camisas en las siguientes cantidades: \(x\), \(y\) y \(z\). El tipo 1 tiene un costo de $ 1, el tipo 2 un costo de $ 1.2 y el tipo 3 un costo de $ 1.5. Además, se necesitan 1 hora para producir el tipo 1, 0,5 horas para producir el tipo 2 y 0,8 horas para el tipo de producto 3.

Sé que tengo $ 800 para gastar y 500 horas disponibles. Además, según mis estimaciones de demanda, quiero producir un total de camisetas tipo 1 que sea la ecuación del total combinado de tipo 2 y tipo 3.

Escribe un sistema de ecuaciones basado en estas restricciones. ¿Es este sistema lineal?

RESPONDER:

Observe que hay tres incógnitas (\(x\), \(y\) y \(z\)), que corresponden a la cantidad de camisas de cada tipo que deben producirse. Además, tenemos tres ecuaciones: una para el costo, otra para la cantidad de horas disponibles y otra para la restricción de la cantidad de camisetas tipo 1 y los demás tipos.

Las siguientes ecuaciones representan la situación:

Usando la convención de dejar todos los términos que dependen de las incógnitas en el lado izquierdo, reescribimos la última ecuación para obtener:

Observe que cada ecuación es lineal, entonces el sistema es un sistema de ecuaciones lineales.

¿Cómo resuelves sistemas de igualdades en general?

Como se mencionó anteriormente, no existe una única estrategia que se ajuste a todos los casos. Solo en el caso de sistemas lineales de ecuaciones habrá una estrategia clara y bien definida.

Aún así, existen algunas buenas prácticas o pasos que debes seguir que pueden ayudarte a resolver todo tipo de sistemas de ecuaciones:

Paso 1: Identifica cada ecuación en el sistema

Paso 2: Mueva a un lado de la ecuación todos los términos que dependen de las incógnitas (generalmente al lado izquierdo) y las constantes al otro lado

Paso 3: Simplifique tanto el lado izquierdo (con las incógnitas) como el lado derecho (con las constantes)

Paso 4: Identifica la estructura de las ecuaciones. ¿Son las ecuaciones lineales o no lineales?

Paso 5: Si todas las ecuaciones son lineales, utilice una de las formas sistemáticas de resolver sistemas lineales (regla de Cramer, sustitución, eliminación, reducción de Gauss, etc.)

Paso 6: Si al menos una ecuación no es lineal, puede intentar utilizar el método de sustitución, comenzando por la ecuación más simple.

Más sobre sistemas de ecuaciones

El sistema de ecuaciones aparece en todas partes en matemáticas, en todas las materias. Ser capaz de resolver sistemáticamente sistemas de ecuaciones demostrará ser una habilidad crucial de dominar.

El sistema más típico que encontrará es un sistema de ecuaciones lineales. Y con frecuencia, encontrará sistemas de ecuaciones lineales, con dos ecuaciones y dos incógnitas. Estos sistemas se suelen llamar sistema de ecuaciones lineales 2x2.

Sistema de ecuaciones gráficas

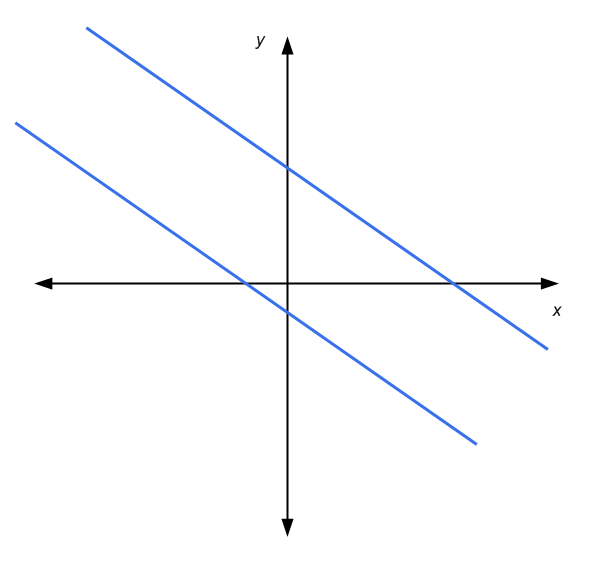
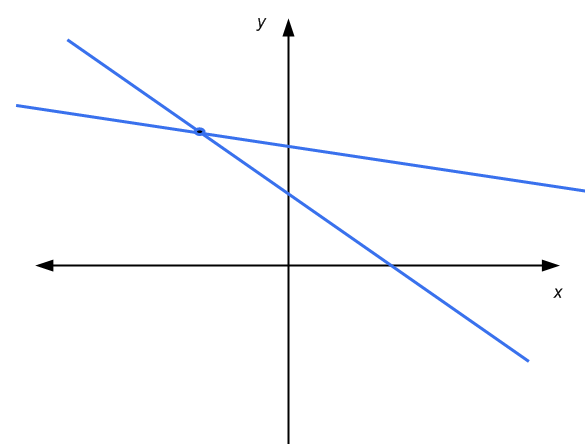
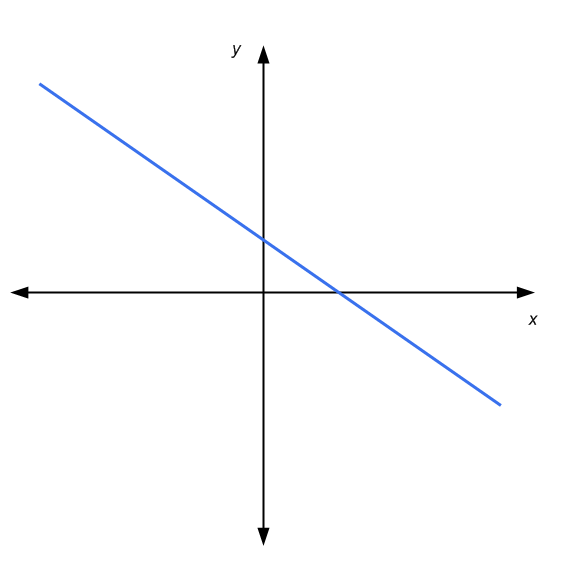
Para el sistema 2x2 de ecuaciones lineales, tenemos la ventaja de poder utilizar una representación gráfica en los ejes coordinados. Una ecuación lineal está representada por una línea en el plano x-y. Gráficamente, la solución de un sistema 2x2 es el punto donde las dos líneas se cruzan, si las hay.

Entonces, en este caso tenemos que: las líneas son paralelas y no se tocan entre sí (sin soluciones), las líneas se cruzan en un punto (solución única), o las líneas son paralelas y se tocan entre sí (infinitas soluciones )

Calculadora de sistema de ecuaciones

Usa este solucionador si quieres resolver un sistema de ecuaciones lineales 2x2 . Esta calculadora usa la regla de Cramer para resolver sistemas 2x2. Para sistemas de ecuaciones más grandes, la mejor alternativa es utilizar la Método de eliminación gaussiano , que trata sistemáticamente con sistemas lineales de cualquier tamaño.