Regla de Cramer
La regla de Cramer es una técnica que se usa para resolver sistemáticamente sistemas de ecuaciones lineales, basados en el cálculo de determinantes.
Normalmente, resolviendo sistemas de ecuaciones lineales puede ser complicado para sistemas que son más grandes que 2x2, porque hay muchas formas de evitar reducirlo cuando hay tres o más variables.
La regla de Cramer proporciona una forma inequívoca y sistemática de encontrar soluciones a sistemas de ecuaciones lineales, sin importar el tamaño del sistema.
El número de cálculos necesarios aumenta para los sistemas grandes, pero el procedimiento es exactamente el mismo, independientemente del tamaño del sistema.
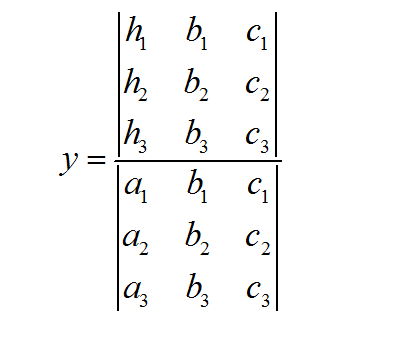
Cómo utilizar la regla de Cramer
Para facilitar las cosas, resolveremos el caso de \(n = 2\) y luego estableceremos una versión más general que, con suerte, tendrá más sentido después de haber abordado el caso \(n=2\).
Paso 1
: Todos los sistemas lineales 2x2 se pueden escribir de la siguiente forma:
Entonces, su primer paso es encontrar estos valores \(a_1, b_1, c_1\) y \(a_2, b_2, c_2\) para el sistema que desea resolver.
Paso 2
: Una vez que tenga los coeficientes \(a_1, b_1, c_1\) y \(a_2, b_2, c_2\), use las siguientes fórmulas para resolver \(x\) y \(y\):
En la fórmula anterior, donde dice "det", significa el determinante de la matriz correspondiente. A veces, se usa una notación más compacta para los determinantes, como se muestra a continuación:
\[\large \displaystyle \det \left[\begin{matrix} a_1 & b_1 \\ a_2 & b_2 \end{matrix}\right] = \left|\begin{matrix} a_1 & b_1 \\ a_2 & b_2 \end{matrix}\right| \]Entonces, usando la notación anterior, obtendríamos estas fórmulas más compactas para la regla de Cramer:
\[\large \displaystyle x = \frac{ \left|\begin{matrix} c_1 & b_1 \\ c_2 & b_2 \end{matrix}\right| }{\left|\begin{matrix} a_1 & b_1 \\ a_2 & b_2 \end{matrix}\right|} \] \[\large \displaystyle y = \frac{ \left|\begin{matrix} a_1 & c_1 \\ a_2 & c_2 \end{matrix}\right| }{\left|\begin{matrix} a_1 & b_1 \\ a_2 & b_2 \end{matrix}\right|} \]Tengamos una forma visual de entender lo que está sucediendo. Observe que tanto \(x\) como \(y\) tienen el mismo determinante en el denominador.
Los coeficientes de esa matriz común utilizada en el denominador se derivan directamente de los coeficientes que multiplican \(x\) y \(y\) en el sistema. Vea la imagen a continuación:
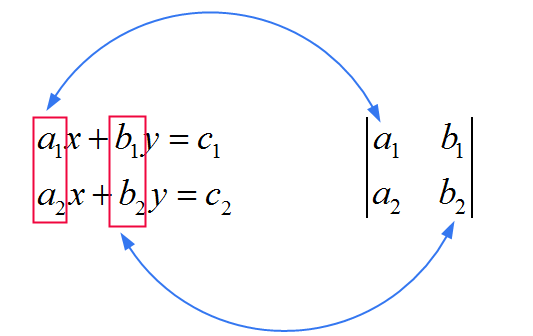
Ahora vemos que \(x\) y \(y\) difieren en lo que tienen en el numerador. Como una forma de recordar la regla, piense en esto:
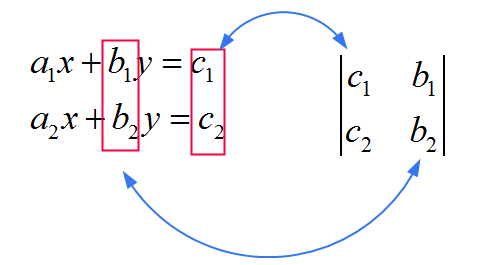
Para \(x\), usa la MISMA matriz que la del denominador, solo que reemplaza la PRIMERA columna con los coeficientes \(c_1\) y \(c_2\). Ver la imagen de abajo
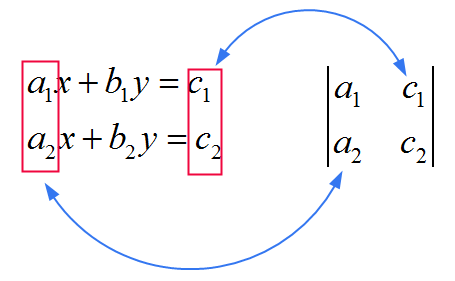
Para \(y\), usa la MISMA matriz que la del denominador, solo que reemplaza la SEGUNDA columna con los coeficientes \(c_1\) y \(c_2\). Ver la imagen de abajo
EJEMPLO 1
Resuelve el siguiente sistema lineal 2x2:
\[\large 2x + 8y = 10\] \[\large 2x - 4y = 4\]RESPONDER:
Sigamos los dos pasos que hemos delineado anteriormente para usar la regla de Cramer para resolver el sistema anterior:
Paso 1
: Necesitamos identificar los coeficientes de los determinantes correspondientes.
Para la matriz que va en el denominador usamos
\[ \left|\begin{matrix} a_1 & b_1 \\ a_2 & b_2 \end{matrix}\right| = \left|\begin{matrix} 2 & 8 \\ 2 & -4 \end{matrix}\right| \]Ahora, en este caso \(c_1 = 10, c_2 = 4\), para el determinante usado para calcular \(x\), reemplazamos la matriz anterior cambiando la PRIMERA columna:
\[ \left|\begin{matrix} c_1 & b_1 \\ c_2 & b_2 \end{matrix}\right| = \left|\begin{matrix} 10 & 8 \\ 4 & -4 \end{matrix}\right| \]Para el determinante usado para calcular \(y\) reemplazamos la matriz anterior cambiando la SEGUNDA columna:
\[ \left|\begin{matrix} a_1 & c_1 \\ a_2 & c_2 \end{matrix}\right| = \left|\begin{matrix} 2 & 10 \\ 2 & 4 \end{matrix}\right| \]Entonces ahora obtenemos la solución:
\[\large \displaystyle x = \frac{ \left|\begin{matrix} c_1 & b_1 \\ c_2 & b_2 \end{matrix}\right| }{\left|\begin{matrix} a_1 & b_1 \\ a_2 & b_2 \end{matrix}\right|} \] \[ = \frac{\left|\begin{matrix} 10 & 8 \\ 4 & -4 \end{matrix}\right|}{\left|\begin{matrix} 2 & 8 \\ 2 & -4 \end{matrix}\right|} = \frac{10 \times (-4) - 4\times 8}{2 \times (-4) - 2 \times 8} = \frac{-72}{-24} = 3 \]y para \(y\):
\[\large \displaystyle y = \frac{ \left|\begin{matrix} a_1 & c_1 \\ a_2 & c_2 \end{matrix}\right| }{\left|\begin{matrix} a_1 & b_1 \\ a_2 & b_2 \end{matrix}\right|} \] \[ = \frac{\left|\begin{matrix} 2 & 10 \\ 2 & 4 \end{matrix}\right|}{\left|\begin{matrix} 2 & 8 \\ 2 & -4 \end{matrix}\right|} = \frac{2 \times 4 - 2\times 10}{2 \times (-4) - 2 \times 8} = \frac{-12}{-24} = \frac{1}{2} \]Por lo tanto, la solución es \(x = 3\), \(y = 1/2\).
Regla de Cramer para el caso general
La belleza de la regla de Cramer es que aplica exactamente el mismo procedimiento, ya sea un sistema 2x2 o un sistema 10x10. El concepto es el mismo.
Entonces, suponga que \(x_1, x_2, ..., x_n\) son las variables (las incógnitas), y queremos resolver el siguiente sistema n x n de ecuaciones lineales:
\[\large a_{11} x_1 + a_{12} x_2 + .... + a_{1n} x_n = c_1 \] \[\large a_{21} x_1 + a_{22} x_2 + .... + a_{2n} x_n = c_2 \] \[\large \vdots \] \[\large a_{n1} x_1 + a_{n2} x_2 + .... + a_{nn} x_n = c_n \]Para resolver \(x_1, x_2, ..., x_n\), usaremos el siguiente determinante en el denominador:
\[\large\displaystyle \left|\begin{matrix} a_{11} & a_{12} & ... & a_{1n} \\ a_{21} & a_{22} & ... & a_{2n} \\ \vdots & \vdots & ... & \vdots\\ a_{n1} & a_{n2} & ... & a_{nn}\end{matrix}\right|\]• La solución para \(x_1\) es
\[\large\displaystyle x_1 = \frac{ \left|\begin{matrix} c_1 & a_{12} & ... & a_{1n} \\ c_2 & a_{22} & ... & a_{2n} \\ \vdots & \vdots & ... & \vdots\\ c_n & a_{n2} & ... & a_{nn}\end{matrix}\right| }{\left|\begin{matrix} a_{11} & a_{12} & ... & a_{1n} \\ a_{21} & a_{22} & ... & a_{2n} \\ \vdots & \vdots & ... & \vdots\\ a_{n1} & a_{n2} & ... & a_{nn}\end{matrix}\right|} \]• La solución para \(x_2\) es
\[\large\displaystyle x_1 = \frac{ \left|\begin{matrix} a_{11} & c_1 & ... & a_{1n} \\ a_{21} & c_2 & ... & a_{2n} \\ \vdots & \vdots & ... & \vdots\\ a_{n1} & a_{n2} & ... & c_n \end{matrix}\right| }{\left|\begin{matrix} a_{11} & a_{12} & ... & a_{1n} \\ a_{21} & a_{22} & ... & a_{2n} \\ \vdots & \vdots & ... & \vdots\\ a_{n1} & a_{n2} & ... & a_{nn}\end{matrix}\right|} \]Y así. Como puede ver, el determinante en el denominador es el mismo, y el del numerador se obtiene cambiando la primera columna con \((c_1, ..., c_n)\) por \(x_1\). Para \(x_2\) cambiamos la segunda columna por \((c_1, ..., c_n)\), para \(x_3\) cambiamos la tercera columna, y así sucesivamente. Entiendes la idea.
EJEMPLO 2
Resuelva el siguiente sistema de ecuaciones lineales 3x3 usando la regla de Cramer.
\[\large x_1 + x_2 + x3 = 20\] \[\large x_1 - x_2 + x3 = 4\] \[\large 2x_1 + x_2 - x3 = 16\]RESPONDER:
En primer lugar, identificamos el determinante que va en el denominador:
\[\large\displaystyle \left|\begin{matrix} 1 & 1 & 1 \\ 1 & -1 & 1 \\ 2 & 1 & -1 \end{matrix}\right|\]Además, necesitamos identificar el vector de coeficientes \(c_i\):
\[\large\displaystyle \left[\begin{matrix} 20 \\ 4 \\ 16 \end{matrix}\right]\]Este vector será el que irá reemplazando las columnas correspondientes del determinante común del denominador. Obtenemos:
\[\large\displaystyle x_1 = \frac{ \left|\begin{matrix} 20 & 1 & 1 \\ 4 & -1 & 1 \\ 16 & 1 & -1 \end{matrix}\right| }{ \left|\begin{matrix} 1 & 1 & 1 \\ 1 & -1 & 1 \\ 2 & 1 & -1 \end{matrix}\right| } = \frac{40}{6} = \frac{20}{3}\] \[\large\displaystyle x_2 = \frac{ \left|\begin{matrix} 1 & 20 & 1 \\ 1 & 4 & 1 \\ 2 & 16 & -1 \end{matrix}\right| }{ \left|\begin{matrix} 1 & 1 & 1 \\ 1 & -1 & 1 \\ 2 & 1 & -1 \end{matrix}\right| } = \frac{40}{6} = \frac{20}{3}\] \[\large\displaystyle x_3 = \frac{ \left|\begin{matrix} 1 & 1 & 20 \\ 1 & -1 & 4 \\ 2 & 1 & 16 \end{matrix}\right| }{ \left|\begin{matrix} 1 & 1 & 1 \\ 1 & -1 & 1 \\ 2 & 1 & -1 \end{matrix}\right| } = \frac{40}{6} = \frac{20}{3}\]Más sobre la regla de Cramer
La regla de Cramer tiene un papel específico en la resolución eficiente de sistemas de ecuaciones lineales. Implica el uso de determinantes para simplificar una tarea que de otra manera sería realmente complicada, especialmente para sistemas más grandes.
En última instancia, para resolver sistemas lineales , todo lo que tiene que hacer es identificar los determinantes de una matriz numérica basada en el sistema que necesita ser resuelto y realizar una operación algebraica simple para resolver el sistema.
Aplicaciones
La regla de Cramer tiene muchas aplicaciones tanto en álgebra lineal como en ecuaciones diferenciales.