Fórmula de elasticidad del arco para una mesa

La fórmula de arco-elasticidad de la demanda permite estimar la elasticidad en los puntos dados en una tabla de programación de demanda, sin tener una fórmula explícita para la función de demanda.

Lo que debe proporcionar es una tabla con una columna para el precio y una columna para la cantidad demandada. Una vez que haya escrito o pegado eso en la hoja de cálculo proporcionada, haga clic en "Calcular" para obtener las elasticidades de arco correspondientes.

Obsérvese que esto es sólo una aproximación: la situación ideal es Calcular elasticidades utilizando la función de demanda , mediante el uso de derivados.

Pasos para utilizar arc-elasticity para una tabla

El fórmula de elasticidad del arco es:

\[ \varepsilon_{ARC} = \displaystyle \left(\frac{Q_2 - Q_1}{P_2 - P_1}\right) \left(\frac{P_1 + P_2}{Q_1 + Q_2}\right)\]

y esto se puede aplicar a puntos consecutivos en una tabla de programación de demanda. Seguirá estos pasos:

• Paso 1: Tabule correctamente sus valores de precio (P) y cantidad demandada (Q)
• Paso 2: Puede crear columnas para Q2 - Q1, P2 - P1, Q1 + Q2 y P1 + P2 si desea que los cálculos sean más claros, o puede calcular la fórmula directamente
• Paso 3: Habrá un punto omitido en la tabla, ya que la elasticidad del arco toma un punto en la tabla y el punto que sigue inmediatamente en la tabla

El uso de esta aproximación de elasticidad de arco le proporcionará una excelente imagen de la sensibilidad a los cambios de precio para el bien específico que se está analizando, aunque sea solo una aproximación.

Cuantos más puntos de demanda tengamos, mejor será la aproximación, especialmente si esos puntos de precio están próximos entre sí.

¿qué mide la elasticidad del arco?

La elasticidad de arco tiene como objetivo proporcionar una aproximación de la elasticidad real en un punto determinado. La elasticidad real a partir de la curva de demanda se calcula mediante:

\[ \varepsilon = \displaystyle \frac{dQ}{dP} \cdot \frac{P}{Q}\]

Se podría argumentar que la elasticidad del arco es solo una aproximación, y entonces, ¿cómo puede tener algún valor? La respuesta a eso es que, para el análisis de elasticidad y, en general, para el análisis de sensibilidad en economía, nos interesan más los rangos que los puntos muy específicos.

De hecho, para fines de microeconomía, es útil saber si estamos en un rango inelástico o no, en lugar del valor muy específico de la elasticidad

No es que el valor específico no sea importante, ya que de hecho es bueno tenerlo, pero las elasticidades de arco son a menudo una buena aproximación y nos darán representaciones muy precisas de a qué tipo de rango de elasticidad nos enfrentamos.

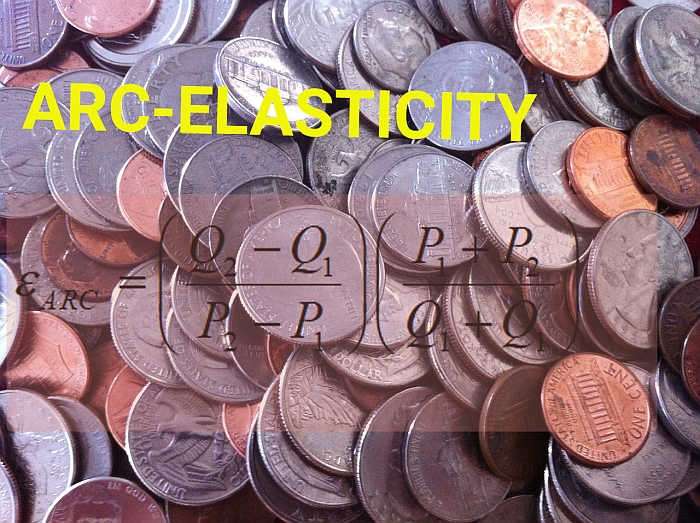
Ejemplo

Considere la siguiente tabla de demanda con información sobre el precio y la cantidad demandada

Proporcione la aproximación de elasticidad del arco para los puntos de datos en esta tabla.

Pag	Q
1	200
1.5	190
2	170
2.5	155
3	130
3.5	110
4	90
4.5	60

Solución: Para aproximar la elasticidad precio de la demanda a partir de estos datos, necesitamos utilizar la siguiente fórmula de elasticidad de arco

\[ \varepsilon_{ARC} = \displaystyle \left(\frac{Q_2 - Q1}{P2_P1}\right)\left(\frac{P_1 + P_2}{Q_1 + Q_2}\right)\]

Aplicando la fórmula anterior a todos los pares de puntos de datos consecutivos, encontramos las siguientes arco-elasticidades:

Pag	Q	Elasticidad Del Arco
1	200	-
1.5	190	\(\left(\frac{ 190 - 200}{ 1.5 - 1}\right) \left(\frac{ 1 + 1.5}{ 200 + 190}\right) = -0.13\)
2	170	\(\left(\frac{ 170 - 190}{ 2 - 1.5}\right) \left(\frac{ 1.5 + 2}{ 190 + 170}\right) = -0.39\)
2.5	155	\(\left(\frac{ 155 - 170}{ 2.5 - 2}\right) \left(\frac{ 2 + 2.5}{ 170 + 155}\right) = -0.42\)
3	130	\(\left(\frac{ 130 - 155}{ 3 - 2.5}\right) \left(\frac{ 2.5 + 3}{ 155 + 130}\right) = -0.96\)
3.5	110	\(\left(\frac{ 110 - 130}{ 3.5 - 3}\right) \left(\frac{ 3 + 3.5}{ 130 + 110}\right) = -1.08\)
4	90	\(\left(\frac{ 90 - 110}{ 4 - 3.5}\right) \left(\frac{ 3.5 + 4}{ 110 + 90}\right) = -1.5\)
4.5	60	\(\left(\frac{ 60 - 90}{ 4.5 - 4}\right) \left(\frac{ 4 + 4.5}{ 90 + 60}\right) = -3.4\)

Interpretación

La tabla que se encuentra muestra la elasticidad precio aproximada de la demanda para cada uno de los puntos de precio proporcionados. Estos valores se pueden utilizar de manera aproximada para determinar los rangos elásticos e inelásticos para la tabla de demanda proporcionada.

Otras calculadoras económicas

Si trabajas en Econometría, esto Calculadora de regresión Probablemente será útil, especialmente porque muestra todos los pasos del proceso de cálculo de coeficientes de regresión .

También puedes utilizar un ecuación logarítmica para estimar un curva de demanda con elasticidad constante .