Aprender a encontrar el dominio de una función es una habilidad crucial en Álgebra, porque le brinda la capacidad de evaluar dónde está definida correctamente una función. O en otras palabras, la región donde es válido operar la función

La tarea de encontrar dónde es válido operar una función es útil. Por ejemplo, considere la función \(f(x) = \sqrt x\). Sabemos que la función opera valores tales que \(x \ge 0\). No podemos trabajar con números negativos, porque obtendríamos algo como \(f(-1) = \sqrt{-1}\), que no está bien definido (al menos como un número real)

Puedes consultar nuestro tutorial anterior en el que hablamos en profundidad sobre el dominio y rango . Este tutorial estará orientado hacia la parte operativa de encontrar el dominio.

¿Por qué necesitamos encontrar el dominio?

La razón por la que necesitamos encontrar el dominio de una función es que cada función tiene un conjunto específico de valores donde se define. No todas las funciones están definidas en todas partes de la línea real.

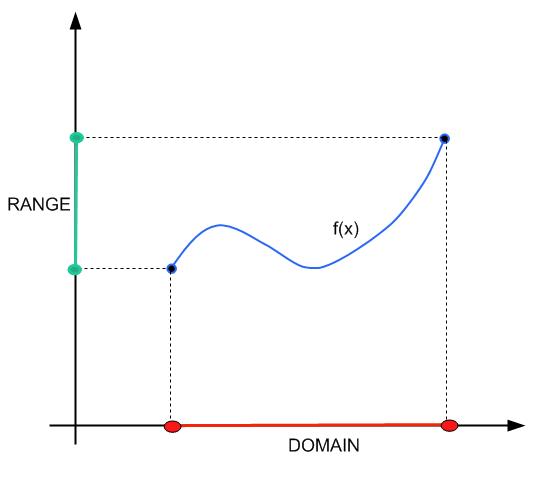
El dominio de la región en la línea real donde está válido para trabajar con la función \(f(x)\), en términos de los valores que puede tomar \(x\).

¿Qué debemos hacer para encontrar el dominio?

Realmente, no hay un truco que se adapte a todos los tamaños. Cada función es diferente y es necesario utilizar diferentes estrategias para encontrar el dominio, según la función.

Hay dos técnicas que SIEMPRE debes tener en cuenta:

Técnica 1 : Asegúrese de que haya divisiones entre cero.

Además, los puntos que conducen a una división por cero deben excluirse del dominio.

Técnica 2 : Asegúrese de que haya raíces cuadradas de división con argumentos negativos (como \(\sqrt{-1}\)).

Además, los puntos que conducen a una raíz cuadrada de un número negativo deben excluirse del dominio.

En última instancia, con estas dos técnicas, debería poder eliminar los puntos que no están en el dominio. El resto de puntos de la línea real SON parte del dominio, simplemente.

Entonces, estas dos técnicas resuelven el problema de saber cómo encontrar el dominio de una función algebraicamente. Otra forma de hacerlo es mirando el gráfico, si está disponible.

EJEMPLO 1

Encuentra el dominio de la función \(f(x) = \sqrt{x+4}+3\)

RESPONDER:

Lo primero que debemos hacer, y es ahí donde radica nuestro éxito en la búsqueda del dominio, es determinar dónde podríamos encontrar potencialmente operaciones no válidas, como divisiones entre cero o raíces cuadradas negativas.

Para la función \(f(x) = \sqrt{x+4}+3\), no hay divisiones potenciales entre cero, pero hay una raíz cuadrada. Para tener un argumento válido, el argumento dentro de la raíz cuadrada debe ser no negativo.

Por lo tanto, para que \(x\) esté en el dominio de la función, necesitamos tener \(x\ge 0\). Esto implica que el dominio de \(f\) es \(\{x: x\ge 0\}\), o \([0, +\infty)\) si usamos notación de intervalo.

¿Siempre es así de fácil? En realidad, no, puede ser tan difícil como parece, dependiendo de la complejidad de la función \(f(x)\).

Normalmente, sin embargo, los ejemplos que ve en sus exámenes y tareas son bastante simples. Vamos a alcanzar un nivel más alto en términos de dificultad.

EJEMPLO 2

Ahora encuentre el dominio de la función \(\displaystyle f(x) = \sqrt{\frac{x+4}{x-3}}\)

RESPONDER:

Esta función es un poco más compleja y requiere un tratamiento más cuidadoso. En este caso, debemos preocuparnos por las posibles divisiones entre cero y las raíces cuadradas negativas.

Primero, podría haber una posible división por cero, cuando \(x = 3\), lo que indica que \(x = 3\) debe excluirse del dominio.

Ahora, debemos ocuparnos de una posible raíz cuadrada negativa. Necesitamos evaluar el signo de \(\displaystyle \frac{x+4}{x-3}\). Además, necesitamos que no sea negativo, por lo que debemos resolver:

Para que una división no sea negativa, necesitamos que tanto el numerador como el denominador sean positivos, o que tanto el numerador como el denominador sean negativos.

En otras palabras, necesitamos tanto \(x+4 \ge 0\) como \(x-3 > 0\), o ambos \(x+4 \le 0\) y \(x-3 < 0\).

Esto es lo mismo que \(x \ge -4\) y \(x > 3\), o ambos \(x \le -4\) y \(x < 3\).

Y esto se puede escribir como \(x > 3\), o ambos \(x \le -4\), que corresponde al intervalo \( (-\infty, -4] \cup (3, +\infty)\).

La conclusión es que el dominio de la función \(\displaystyle f(x) = \sqrt{\frac{x+4}{x-3}}\) es:

Como puede ver, el nivel de dificultad aumentó un poco y, de hecho, puede aumentarlo tanto como desee.

Cómo encontrar el dominio de una función racional

Antes que nada, recordemos que una función racional es el cociente de dos polinomios, de la forma:

¿Cómo encuentras el dominio de la función racional anterior? Necesitamos seguir nuestra regla: busque divisiones potenciales entre cero y raíces cuadradas negativas.

En este caso, no hay raíces cuadradas negativas potenciales, pero podría haber divisiones entre cero, siempre que el polinomio que está en el denominador sea cero.

La conclusión es muy simple: el dominio de una función racional es la recta real completa EXCEPTO aquellos puntos en los que el polinomio en el denominador es cero.

EJEMPLO 3

Encuentra el dominio de

RESPONDER:

En primer lugar, debemos entender que esta es una función racional, porque tiene dos polinomios \(p(x) = x^2 + x + 1\) y \(q(x) = x^3 - 6x^2 + 11x - 6\) en el numerador y denominador, respectivamente.

Entonces, el primer paso es encontrar los ceros del polinomio en el denominador, así que necesitamos resolver: \[ x^3 - 6x^2 + 11x - 6 = 0\]

Esa ecuación es algo difícil de resolver, así que te daré que de hecho \(x^3 - 6x^2 + 11x - 6 = (x-1)(x-2)(x-3)\), entonces tenemos que resolver:

lo que significa que las raíces del polinomio en el denominador son \(x_1 = 1, x_2 = 2, x_3 = 3\). La conclusión es que el dominio de la función es toda la línea real, excepto los puntos 1, 2 y 3. Usando la notación de intervalo, el dominio es \((-\infty, +\infty) \backslash \{1,2,3\}\).

Otras estrategias para encontrar el dominio de una función

La alternativa de encontrar el dominio de una función observando las posibles divisiones entre cero o raíces cuadradas negativas, que es la forma analítica, es mirar la gráfica.

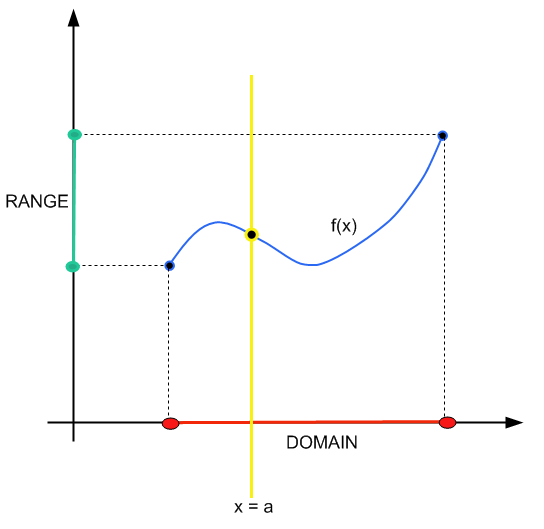
El método es simple: construyes una línea vertical \(x = a\). Si esa línea vertical cruza la gráfica de la función en uno y solo un punto, entonces \(x = a\) pertenece al dominio.

Corto y dulce.

Finalmente, ¿cómo se encuentra el dominio de una función con raíz cuadrada?

Este es el núcleo de una de las técnicas de las que hemos estado hablando, que es encontrar posibles raíces cuadradas negativas. Entonces, cuando tienes una función con una o más raíces cuadradas, sabes que es muy probable que tengas una raíz negativa potencial y necesitas detectarla.

Sin embargo, este no siempre es el caso. Piense en la función \(f(x) = \sqrt{x^2}\). Esa función tiene una raíz cuadrada, pero el argumento interior es \(x^2\), que no puede ser negativo, por lo que tenemos el caso de una función con una raíz cuadrada que no tiene raíces cuadradas negativas.