Cómo encontrar el rango
Aprender a encontrar el rango de una función puede resultar muy importante en Álgebra y Cálculo, porque te da la capacidad de evaluar qué valores alcanza una función. O en otras palabras, te permite encontrar el conjunto de todas las imágenes a través de la función
La tarea de encontrar qué puntos se pueden alcanzar con una función es muy útil. Por ejemplo, puede tener una función de producción \(q(x)\), que le da la cantidad de salida obtenida para \(x\) unidades de entrada.
Nos gustaría saber cuántas unidades de entrada se necesitan para producir \(b\) unidades de salida. Entonces, en otras palabras, necesitamos encontrar \(x\) para que \(q(x) = b\), que es otra forma de preguntar si \(b\) está o no en el rango de la función \(q(x)\).
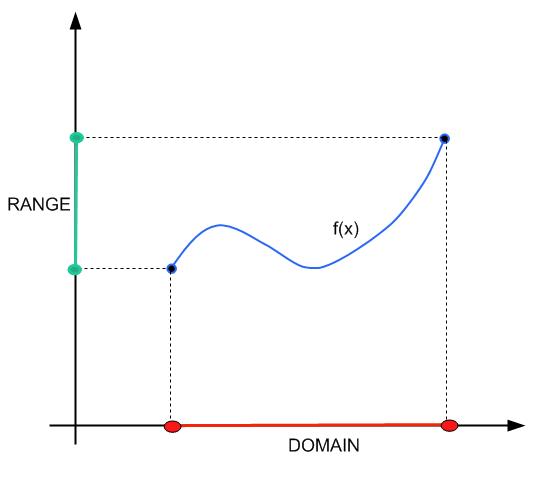
En este tutorial nos concentraremos más en la mecánica de encontrar el rango. Para un enfoque más conceptual del dominio y el rango, puede tutorial mira este .
La forma algebraica de encontrar el rango de una función
Igual que cuando aprendimos a calcular el dominio, no hay una receta para encontrar el rango, realmente depende de la estructura de la función \(f(x)\).
Sin embargo, hay una técnica algebraica que siempre se utilizará. Esta es la forma en que encuentra el rango. Presta atención:
Digamos que necesitamos obtener el rango de una función dada \(f(x)\). Luego, consideraremos un número real genérico \(y\) e intentaremos resolver para \(x\) la siguiente ecuación:
\[f(x) = y\]Necesitamos determinar para qué valores de \(y\) la ecuación anterior se puede resolver para \(x\). Eso es. Por supuesto, eso podría ser difícil de hacer, dependiendo de la estructura de la función \(f(x)\), pero es lo que debe hacer.
Así que esta es la forma algebraica, la forma de encontrar el rango de una función sin graficar.
EJEMPLO 1
Encuentre el rango de la función \(\displaystyle f(x) = \frac{x+1}{x-3}\):
RESPONDER:
Procedemos de la forma algebraica: Sea \(y\) un número y resolveremos \(x\) en la siguiente ecuación: \(f(x) = y\). El valor \(y\) está en el rango si \(f(x) = y\) se puede resolver para \(x\).
En este caso tenemos:
\[\large f(x) = y \Leftrightarrow \frac{x+1}{x-3} = y\] \[\Rightarrow \,\,\,x+1 = y\left( x-3 \right)\] \[\Rightarrow \,\,\,x+1 = yx-3y\] \[\Rightarrow \,\,\,x-yx=-1-3y\] \[\Rightarrow \,\,\,x\left( 1-y \right)=-1-3y\] \[\Rightarrow \,\,\,x=\frac{3y+1}{y-1}\]Por lo tanto, ¿cuándo estará bien definido \(x\)? Casi para todos \(y\), excepto cuando \(y = 1\), porque en ese caso tenemos una división por \(0\). Por lo tanto, el rango de \(f\) en este caso es la línea real completa, excepto 1.
Si usamos notación de intervalo, podemos escribir \(Range(f) = (-\infty, 1) \cup (1, +\infty)\).
EJEMPLO 2
Encuentre el rango de la función \(f(x) = x^2 - 4x + 3\):
RESPONDER:
Nuevamente, procedemos usando la forma algebraica, para que conozca el ejercicio: Sea \(y\) un número y resolveremos \(x\) en la siguiente ecuación: \(f(x) = y\). El valor \(y\) está en el rango si \(f(x) = y\) se puede resolver para \(x\).
En este caso tenemos:
\[\large f(x) = y \Leftrightarrow x^2 - 4x + 3 = y\] \[\Rightarrow \,\,\, x^2 - 4x + 3 - y = 0 \text{ (This is a quadratic equation in x)}\] \[\Rightarrow \displaystyle \,\,\, x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\] \[\Rightarrow \displaystyle \,\,\, x = \frac{-(-4) \pm \sqrt{(-4)^2 - 4(1)(3-y)}}{2(1)}\] \[\Rightarrow \displaystyle \,\,\, x = \frac{4 \pm \sqrt{16 - 4(3-y)}}{2}\] \[\Rightarrow \displaystyle \,\,\, x = \frac{4 \pm \sqrt{16 - 12 + 4y}}{2}\] \[\Rightarrow \displaystyle \,\,\, x = \frac{4 \pm \sqrt{4 + 4y}}{2}\] \[\Rightarrow \displaystyle \,\,\, x = 2 \pm \sqrt{1+y}\]Ahora, viendo esta expresión final, ¿cuándo estará bien definido \(x\)? Necesitamos tener que el argumento de la raíz cuadrada debe ser no negativo, por lo que necesitamos:
\[1+y \ge 0\]lo que significa que \(y \ge -1\). Si usamos la notación de intervalo, podemos escribir \(Range(f) = [-1, +\infty)\).
En este ejemplo, podríamos haberlo resuelto usando el hecho de que \(f(x) = x^2 - 4x + 3\) es una función cuadrática, y su gráfica es una parábola que se abre hacia arriba.
El punto mínimo de esta parábola se alcanza en el vértice. La coordenada x del vértice es:
\[\displaystyle x_V = \frac{-b}{2a} =\frac{-(-4)}{2(1)} =\frac{4}{2} = 2\]Ahora, la coordenada y del vértice se encuentra simplemente reemplazando el valor \(x_V = 2\) en la función cuadrática:
\[y_V = f(x_V) = 2^2 - 4(2) + 3 = -1\]Dado que el valor mínimo alcanzado por la parábola es \(-1\), concluimos que el rango es \([-1, +\infty)\), que es la misma conclusión que la hallada algebraicamente.
El gráfico de la función \(f(x) = x^2 - 4x + 3\) lo deja aún más claro:
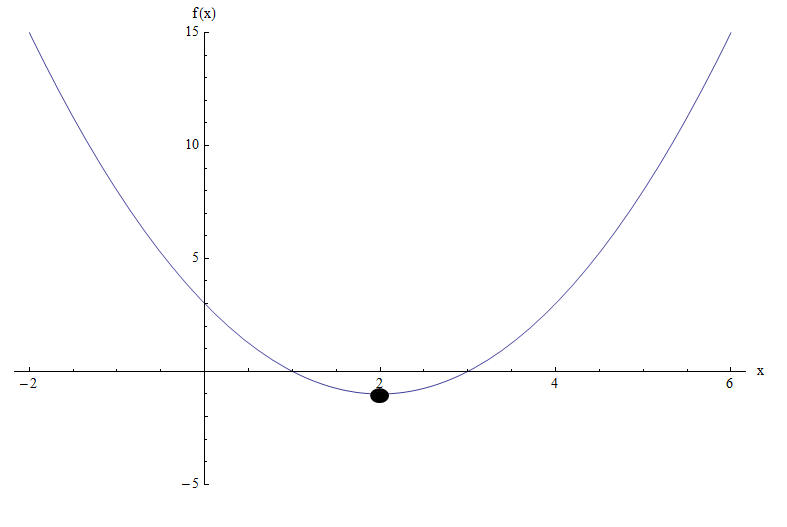
Podemos ver que, según la gráfica, el mínimo se alcanza en \(x = 2\), que es exactamente lo que se encontró en la coordenada x del vértice.
El riesgo de usar el gráfico para encontrar el rango es que podría leer mal los puntos críticos en el gráfico y dar una evaluación inexacta del lugar donde la función alcanza su máximo o mínimo.
Otras estrategias para encontrar el rango de una función
Como vimos en el ejemplo anterior, a veces podemos encontrar el rango de una función con solo mirar su gráfica.
Por ejemplo, digamos que desea encontrar el rango de la función \(f(x) = x + 3\). El gráfico se muestra a continuación:
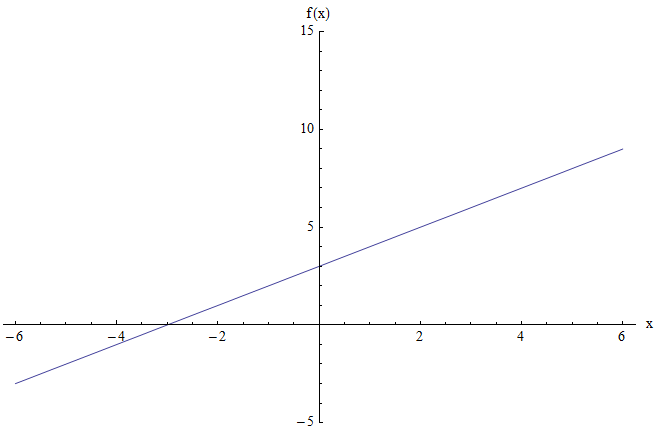
El gráfico anterior no muestra puntos mínimos o máximos. Además, cuando \(x\) es grande y positivo, el valor de la función también es grande y positivo. Y análogamente, cuando \(x\) es muy negativo, el valor de la función también es muy negativo.
La intuición es que la función puede tomar valores tan negativos y positivos como queramos, seleccionando valores \(x\) suficientemente grandes (positivos o negativos). Y luego, la conclusión es que el rango es la línea real completa, que es \((-\infty, +\infty)\) usando notación de intervalo.
Tal análisis es correcto en términos del resultado, pero es endeble en términos de razonamiento. El "método gráfico" para encontrar el rango tiene ese problema: es atractivo desde un punto de vista intuitivo, pero es bastante delgado en términos de contenido.
Normalmente, si es posible, deberíamos preferir la forma analítica / algebraica. En el ejemplo, necesitamos resolver para \(x\):
\[x + 3 = y\] \[\Rightarrow \,\, x = y - 3\]Entonces, ¿hay alguna restricción en \(y\) para que \(x\) esté bien definido? En absoluto, entonces, no hay restricciones en \(y\) y la conclusión es que el rango es toda la línea real.
Puedes consultar este artículo que quieras saber cómo encontrar el dominio de una función en lugar.
Hay muchas buenas razones algebraicas para encontrar el rango, una de ellas es porque es parte de los procesos para encontrar la inversa de una función .
