¿Cuál es la raíz cuadrada de 64?
A veces, una pregunta simple como cuál es la raíz cuadrada de 64 tiene una respuesta que puede confundir a algunos. En este caso, disiparemos un par de mitos.
El objetivo principal de este tutorial es aprender algunas cosas sobre raíces cuadradas y radicales, para que pueda responder preguntas al respecto sin dudarlo.
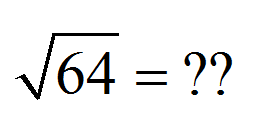
Lo primero es lo primero. Expliquemos la definición de la raíz cuadrada:
La raíz cuadrada de un número dado es la positivo número (o cero) de modo que cuando se eleva al cuadrado da como resultado ese número dado .
Eso es. Entonces, dado un número \(x\), su raíz cuadrada es un número \(b\) de modo que \(b \ge 0\) y
\[b^2 = x\]Al observar la expresión anterior, podemos ver que si \(b\) va a ser la raíz cuadrada de \(x\), entonces \(x = b^2\), y dado que un número cuadrado no puede ser negativo, \(x\) solo puede ser no negativo (si queremos poder encuentra su raíz cuadrada).
Conclusión : Solo podemos calcular raíces cuadradas de valores no negativos \(x\). O dicho de otra manera, el dominio de la función \(\sqrt x\) es \([0,+\infty)\).
Entonces, respondiendo a nuestra pregunta inicial:
¿Cuál es la raíz cuadrada de 64?
Según lo que definimos, necesitamos encontrar un valor no negativo \(b\) para que \(b^2 = 64\). ¿Te viene a la mente algún número que satisfaga esas propiedades?
Bueno, sí, ¿y si probamos con \(b = 8\)? Ok, entonces \(b = 8\) no es negativo y \(b^2 = 8^2 = 64\).
Entonces, hemos encontrado la raíz cuadrada de 64, que es 8, porque 8 no es negativo y \(8^2 = 64\). Escribimos esto como:
\[ \sqrt{64} = 8 \]El mito sobre la función raíz cuadrada
Ahora vamos al tema que motivó este tutorial ... La definición anterior dada de la raíz cuadrada nos permite descartar la afirmación común de que "la raíz cuadrada de 64 es más o menos 8", lo cual es incorrecto. En efecto
\[\sqrt{64} =\not \pm 8\]Ahora, podemos entender por qué ese mito continúa. De hecho, tanto 8 como -8 tienen la propiedad de que \(8^2 = 64\) y \((-8)^2 = 64\). Entonces, ¿por qué -8 NO es la raíz cuadrada de 64?
Porque, por definición, dijimos que la raíz cuadrada debe ser ese número no negativo que tiene la propiedad de que cuando se eleva al cuadrado es igual al número dado. Y -8 falla en la condición de no ser negativo.
La gráfica de la función raíz cuadrada
Mira la gráfica de la función raíz cuadrada a continuación:
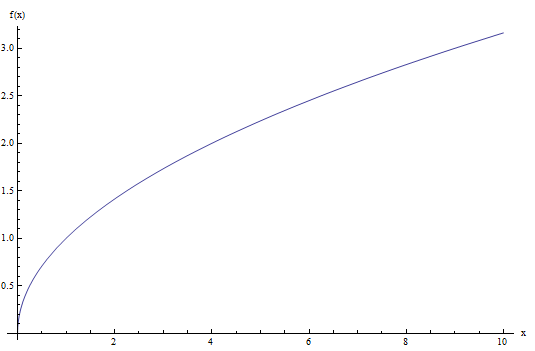
Como puede ver, esa función solo toma valores no negativos y, en realidad, pasa la prueba de la línea vertical, por lo que es una función.
Entonces, al final, la definición de la raíz cuadrada como el \(b\) no negativo para que \(b^2 = x\) haga que la raíz cuadrada sea una función.
Si de hecho tuviéramos que \(\sqrt{64} = \pm 8\), entonces \(\sqrt x\) no sería una función, sería una relación en su lugar, porque la línea vertical en \(x = 64\) cruzaría la gráfica dos veces (en 8 y -8).
¿Qué pasa con otras funciones radicales?
Hay otros tipos de funciones radicales. Por ejemplo, la raíz cúbica \(\sqrt[3] x\). En este caso, no es necesario establecer una regla sobre qué radical elegir, porque la raíz cúbica de un número dado \(x\) es el número \(b\) de modo que \(b^3 = x\).
Raíz cúbica
Para el caso de la raíz cúbica, no es necesario hacer distinciones porque para un \(x\) dado, habrá solo UN número \(b\) tal que \(b^3 = x\).
Por ejemplo
\[\sqrt[3]{64} = 4\]simplemente porque \(4^3 = 64\). O
\[\sqrt[3]{-64} = -4\]simplemente porque \((-4)^3 = -64\). Es decir, no hay ambigüedad como en el caso de la raíz cuadrada.
Raíz cuartica
Para el caso de la raíz cuártica, es similar a la raíz cuadrada. Tendremos ese \(\sqrt[4] x = b\) si \(b \ge 0\) y \(b^4 = x\).
Por ejemplo
\[\sqrt[4]{16} = 2\]porque \(2^4 = 16\) y \(2 \ge 0\). Pero
\[\sqrt[4]{16} =\not -2\]porque aunque \((-2)^4 = -16\), tenemos ese \(-2 < 0\), entonces no se cumple la condición de no negatividad.
¿Qué tal para la raíz n-ésima \(\sqrt[n] x\) en general ???.
Estoy seguro de que lo adivinaste.
Incluso para \(n\), la situación es como la raíz cuadrada: \(\sqrt[n] x = b\) si \(b \ge 0\) y \(b^n = x\).
Para \(n\) impar, la situación es como la raíz cuadrada: \(\sqrt[n] x = b\) si \(b^n = x\).
Más sobre el cálculo de la raíz cuadrada
Una cosa en la que hicimos hincapié fue en que la función de raíz cuadrada \(\sqrt x\) necesita tomar un argumento no negativo \(x\) si queremos poder calcular la raíz cuadrada.
Hicimos un poco de trampa, porque no escribimos la oración completa: La función de raíz cuadrada \(\sqrt x\) necesita tomar un argumento no negativo \(x\) si queremos poder calcular la raíz cuadrada en la LÍNEA REAL.
PERO, si \(x < 0\), esto es, si \(x\) es negativo, entonces \(\sqrt x\) todavía está definido, pero no como un número real sino como un número complejo.
La unidad básica de la raíz cuadrada compleja es la raíz cuadrada de -1. ¿Qué es \(\sqrt{-1}\) ???
Ingrese los números complejos: Hay un número complejo, llamado \(i\) para que
\[\sqrt{-1} = i \]A partir de ese momento, las propiedades de la raíz cuadrada funcionan igual. Por ejemplo:
\[\sqrt{-4} = \sqrt{4} \sqrt{-1} = 2\sqrt{-1} = 2i \]