Más información sobre este creador de gráficos xbar

Esta calculadora de gráficos de barras en X le mostrará todos los pasos necesarios para construir un gráfico de barras en X, que es uno de los gráficos más comunes utilizados para evaluar si un proceso está en control o no.

Esto se consigue identificando gráficamente los puntos que presentan un nivel de variación que parece ir estadísticamente más allá de lo que se consideraría una "causa común".

¿qué fórmulas se utilizan para un gráfico de barras x?

En este caso asumimos que tenemos muestras \(N\) y que cada muestra tiene un tamaño de \(k\) (donde normalmente \(N\) es mucho más grande que \(k\).

Entonces, para cada muestra \(i\) calculamos su media muestral \(\bar X_i\) y su rango muestral \(R_i\). Luego, tomas el promedio de ellos para obtener \(\overline{\overline X}\) y \(\bar R\)

A continuación, utilice la siguiente fórmula para obtener el límite de control inferior y superior para el gráfico de barras X

\[ LCL_{\bar X} = \overline{\overline X} - A_2 \bar R \] \[ UCL_{\bar X} = \overline{\overline X} + A_2 \bar R \]

donde \(A_2\) es una constante que depende del tamaño de muestra \(k\) de las muestras.

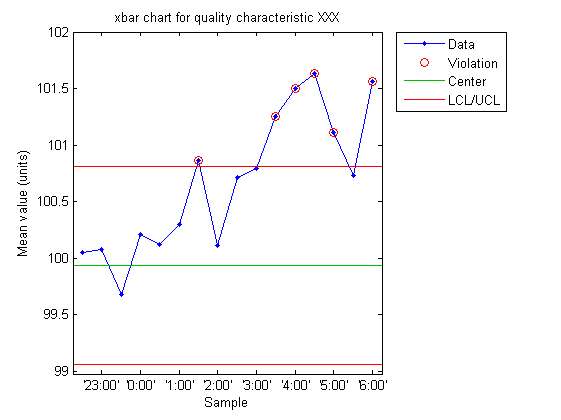
¿cómo se hace un gráfico de barras x?

1. El primer paso es recoger los datos, donde se recogen muestras, y cada muestra tiene el mismo tamaño de muestra.

2. A continuación, se calcula la media y el rango muestral de cada una de las muestras.

3. Se calcula la media general para las medias y el rango de la muestra.

4. Luego, calcula los límites de control \(LCL_{\bar X} = \overline{\overline X} - A_2 \bar R \) y \(UCL_{\bar X} = \overline{\overline X}\) + A_2 \bar R \).

5. Ahora, se traza cada una de las medias muestrales en un gráfico de líneas, y se trazan los límites inferior y superior.

6. Por último, se evalúa si alguna de las medias de la muestra supera los límites de control.

Los puntos que superan los límites de control inferior y superior se consideran fuera de control estadístico. Si ningún punto está fuera de control estadístico, el proceso está controlado.

Otro gráfico de control

El gráfico Xbar se utiliza para evaluar si el centro del proceso está o no en control. Si necesita evaluar si la variabilidad del proceso está en control estadístico, puede utilizar este Creador de gráficos R .

¿se puede hacer un gráfico de barras x en excel?

Sí, hay que construir un gráfico con tres líneas constantes (para los límites inferior, central y superior), y otro gráfico de líneas para el gráfico de las medias muestrales.

Con esta calculadora puedes pegar directamente los datos que tienes en Excel es la hoja de cálculo de arriba, para obtener cálculos automáticos, paso a paso.