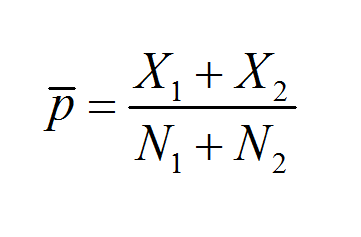Calculadora de proporciones

Esta calculadora te ayudará a calcular una relación de proporcionalidad A/B = C/D, para la que deberás proporcionar tres de las cuatro expresiones numéricas para encontrar la que falta. También puedes proporcionar las cuatro y la calculadora evaluará si la proporcionalidad se cumple o no para los números proporcionados.

Una vez que proporcione las expresiones numéricas solicitadas (que pueden ser números o cualquier expresión numérica válida), puede hacer clic en el botón "Calcular" para ver el resultado de los cálculos.

¿cómo utilizar esta calculadora de proporciones?

Con esta calculadora de proporciones, te resultará más fácil resolver proporciones matemáticas. Estos son los pasos que debes seguir:

• Identificar la proporcionalidad: Establece la proporción que necesitas calcular
• Introduzca los valores conocidos: Ingrese los valores conocidos en los cuadros provistos, necesita tres números de los cuatro números involucrados en la proporción.
• Calcular: Haga clic en el botón Calcular para obtener el resultado. La calculadora le mostrará el valor que falta.

Pasos para resolver proporciones

Aquí se explica cómo puedes resolver proporciones manualmente:

• Establezca la proporción: Escribe las proporciones en forma de fracción, como \(\frac{A}{B} = \frac{C}{D}\).
• Multiplicación Cruzada: Multiplica el numerador de la primera fracción por el denominador de la segunda, y viceversa: \(A \times D = B \times C\).
• Resolver lo desconocido: Si estás resolviendo \(x\), reorganiza la ecuación para aislar \(x\).
• Revisa Tu Trabajo: Asegúrese de que las proporciones sean iguales sustituyendo el valor encontrado en la proporción original.

Fórmula de proporción explicada

La fórmula básica para una proporción es:

\[ \frac{A}{B} = \frac{C}{D} \]

Donde \(A\) y \(B\) son la primera razón, y \(C\) y \(D\) son la segunda razón. Esta fórmula también se puede expresar como si el producto \(B \times C\)) fuera igual al producto \(A \times D\)). Esta relación juega un papel fundamental en la comprensión de cómo funcionan las proporciones.

Tipos de proporciones

Existen varios tipos de proporciones:

• Proporción Directa: Cuando una cantidad aumenta, la otra aumenta al mismo ritmo. Por ejemplo, si se duplica el número de trabajadores, el trabajo realizado también se duplica.
• Proporción Inversa: A medida que una cantidad aumenta, la otra disminuye. Por ejemplo, si aumentas la velocidad de viaje, el tiempo para llegar a un destino disminuye, debido a la fórmula física tiempo = distancia / velocidad.
• Proporción Partitiva: Se utiliza cuando se divide un todo en partes según proporciones dadas.

Proporción directa vs. proporción inversa

Un tema que es muy importante entender es el de la diferencia cuantitativa entre proporciones directas e inversas:

• Proporción Directa: Cuando \(x\) es directamente proporcional a \(y\), tenemos \(x = ky\) donde \(k\) es una constante.
• Proporción Inversa: Cuando \(x\) es inversamente proporcional a \(y\), tenemos \(xy = k\), donde \(k\) es una constante.

Aplicaciones de las proporciones en la vida real

Las proporciones no son sólo una construcción teórica y pueden tener numerosas aplicaciones prácticas, entre ellas:

• Cocinando: Aumentar o reducir la escala de las recetas según la cantidad de porciones.
• Finanzas: Cálculo de tasas de interés o rendimientos de inversiones.
• Construcción: Determinar la cantidad de materiales necesarios para un proyecto.
• Medicamento: Cálculos de dosis según el peso o la edad del paciente.

¿cómo calculo una proporción?

Para calcular una proporción:

• Identifica los valores conocidos en la proporción.
• Establezca la ecuación de proporción.
• Utilice la multiplicación cruzada para resolver la incógnita.
• Verifique su solución sustituyendo nuevamente en la ecuación original.

¿las razones 14:7 y 8:4 forman una proporción?

Necesitamos comprobarlo:

\[ \frac{14}{7} = \frac{8}{4} \]

Simplificando, simplemente obtenemos:

\[ 2 = 2 \]

Lo que implica que ambos lados son iguales. Por lo tanto, sí, las razones 14:7 y 8:4 forman una proporción porque son iguales cuando se simplifican.

¿15, 2 y 4/30 forman una proporción?

Para verificar:

\[ \frac{15}{2} = \frac{4}{30} \]

Simplificando:

\[ \frac{15}{2} = 7.5 \] \[ \frac{4}{30} = \frac{2}{15} = 0.1333 \]

Por lo tanto la respuesta es NO, estos no forman una proporción ya que las razones no son iguales.

Calculadora de proporciones con pasos

Así es como funciona nuestra calculadora de proporciones con pasos:

• Ingrese los valores conocidos, que normalmente son 3 de los 4 valores.
• La calculadora mostrará el proceso paso a paso para resolver la proporción en función de los datos proporcionados, lo que incluye cualquier multiplicación cruzada requerida y la resolución de la variable desconocida.
• Proporcionará la respuesta final para el valor desconocido junto con los pasos tomados para llegar a la respuesta.

Calculadora de proporciones con 2 variables

Cuando se trata de dos variables en una proporción, la situación es ligeramente diferente porque no se puede resolver inmediatamente una variable, sino que se expresa una de las incógnitas en términos de la otra:

• Paso 1: Debes configurar la ecuación con los valores conocidos y las variables.
• Paso 2: Luego, utilizarás la manipulación algebraica para resolver una variable en términos de la otra.
• Paso 3: Finalmente debes ingresar el valor conocido para encontrar la variable desconocida.

Calculadora de proporciones de fracciones

Muchas veces puedes considerar proporciones como fracciones Una calculadora de proporciones fraccionarias ayuda a:

• Convertir fracciones a decimales o porcentajes para una comparación más sencilla.
• Comprobar si las fracciones son equivalentes simplificándolas.
• Resolver fracciones desconocidas en una proporción.

Proporciones en matemáticas

Descubrirás que las proporciones juegan un papel importante en varios campos matemáticos, incluidos los siguientes:

• Geometría: Los triángulos similares y la escala aplicarán directamente las proporciones entre los lados
• Álgebra: Resolver ecuaciones que involucran proporciones. Esto también podría ocurrir en Cálculo, cuando se trabaja con proporciones relacionadas
• Estadística: Se utiliza para comprender distintas relaciones proporcionales en conjuntos de datos. Generalmente se analiza en forma de proporciones de muestra.

Al comprender y aplicar proporciones, puede resolver problemas complejos de matemáticas y situaciones del mundo real con facilidad. Ya sea que esté ajustando una receta, calculando retornos financieros o escalando un plano, las proporciones son su aliado matemático.

Más calculadoras de proporciones

Si trabaja con proporciones, puede que le resulte útil también consultar áreas relacionadas, como las proporciones de muestra Calculadora De Proporción De Muestra Puede ayudarle a comprender cómo funcionan las proporciones y cómo se calculan dentro de una muestra, lo que resulta especialmente útil en el análisis estadístico o cuando se trabaja con encuestas y sondeos.

Además, si su trabajo implica análisis financiero, métricas comerciales o simplemente desea comenzar con los estados financieros y su interpretación, nuestro Calculadora De Índice De Liquidez Rápida Podría ser de interés. Ayuda a evaluar la capacidad de una empresa para cumplir con sus obligaciones a corto plazo con sus activos más líquidos, lo que indirectamente se relaciona con la comprensión de las proporciones en términos financieros.

Por último, para aquellos que a menudo convierten entre diferentes formas de números, nuestro Calculadora de fracción a porcentaje y Calculadora de porcentaje a fracción Puede simplificar estas conversiones, garantizando que tenga las herramientas adecuadas para trabajar con proporciones en varios formatos.