Qué saber sobre esta calculadora de expansión binomial

Esta calculadora de expansión binomial con pasos le dará una muestra clara de cómo calcular la expresión \[(a+b)^n\]

Para los números dados \(a\), \(b\) y \(n\), donde \(n\) es un número entero.La expresión anterior se puede calcular en una secuencia que se llama La expansión binomial, y tiene muchas aplicaciones en diferentes campos de las matemáticas.

La expansión binomial de la orden n

Utilizando enfoques diversos, se ha encontrado la fórmula para una expansión binomial, y es como se muestra a continuación

\[(a+b)^n = a^n + \dbinom{n}{1} a^{n-1} b + \dbinom{n}{1} a^{n-2} b^2 + ... \dbinom{n}{n-1} a b^{n-1} + b^n\]

donde el término \(\dbinom{n}{k}\) computado es:

\[\dbinom{n}{k} = \frac{n!}{k! \times (n-k)!}\]

Este término \(\dbinom{n}{k}\) es comúnmente conocido como el k ^h Coeficiente binomial de una expansión binomial del orden \(n\).Como podemos ver, un La expansión binomial de la orden \(n\) tiene los términos \(n+1\), cuando \(n\) es un entero positivo.

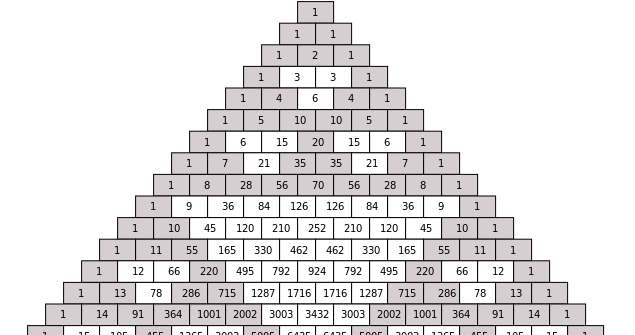
Triángulo de Pascal para una calculadora de expansión binomial PODER NEGATIVO

Una forma muy inteligente y fácil de calcular los coeficientes de una expansión binomial es usar un triángulo que comience con "1" en la parte superior, luego "1" y "1" en la segunda fila.Luego, desde la tercera fila y tome "1" y "1" al principio y al final de La fila, y el resto de los coeficientes se pueden encontrar agregando los dos elementos por encima de él, en la fila inmediatamente arriba, como se muestra en el momento. gráfico a continuación.

Una calculadora de expansión binomial Poderes negativos

Hasta ahora hemos considerado el orden \(n\) para ser un entero positivo, pero también hay una expansión cuando \(n\) es negativo, solo eso no es necesariamente finito, y implicará un número infinito de términos en el caso general.

Coeficientes binomiales

En lugar de computar toda la expansión, use esto. Calculadora de coeficiencia binomial para obtener un término específico de la expansión.