Asíntotas horizontales
En este tutorial cubriremos el concepto de asíntota horizontal y sus aplicaciones más importantes. Intentaremos evitar explicaciones demasiado técnicas, pero se utilizarán algunos toques de Cálculo.
Principalmente, la parte importante que se debe aprender de este tutorial es una fuerte intuición geométrica sobre las asíntotas horizontales. ¡Vamos a empezar!
¿qué es una asíntota horizontal?
Una asíntota horizontal es un límite superior, que puedes imaginar como una línea horizontal que establece un límite para el comportamiento de la gráfica de una función determinada.
Esto significa que la gráfica de la función \(f(x)\) se acerca a esta línea horizontal, a medida que aumenta el valor de \(x\).
¿cómo se encuentra la asíntota horizontal?
Comprender este comportamiento horizontal limitante de funciones que exhiben esta característica puede resultar muy útil para encontrar asíntotas horizontales.
De hecho, en determinadas circunstancias, este comportamiento limitante se parece bastante al de una línea horizontal para valores grandes de \(x\). Vea la función a continuación, por ejemplo.
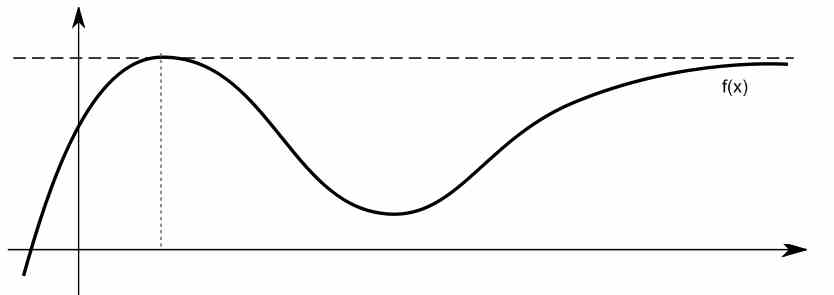
¿cómo se encuentra la asíntota horizontal de una función usando límites?
Para aclarar la definición, una línea horizontal \(y = h\) es una asíntota horizontal de la función \(f(x)\) si
\[\large \lim_{x\to\infty} f(x) = h\]si el límite anterior existe y es finito. Para aquellos que aún no han asistido a una clase de cálculo, la línea horizontal \(y = h\) es una asíntota horizontal de la función \(f(x)\) cuando \(h\) es la límite de \(f(x)\) a medida que \(x\) se acerca al infinito. ¿Qué significa ser un "límite"? Significa que para valores suficientemente grandes de \(x\), el valor de \(f(x)\) será tan cercano a \(h\) como predeterminamos. Fantasía, ¿verdad?
¿cuál es la fórmula de la asíntota horizontal?
Para encontrar la fórmula de la asíntota horizontal, primero debemos encontrar el límite correspondiente. Supongamos que tienes
\[\large \lim_{x\to\infty} f(x) = h\]En ese caso, diremos que la asíntota horizontal es \(h\), y la fórmula para la asíntota horizontal es \(y = h\). En otras palabras, la asíntota horizontal es simple, es una recta horizontal, esta es una recta con pendiente cero.
Esto da el significado a lo que significa una asíntota horizontal en términos de límites: el límite encontrado corresponde a definir la recta horizontal que se llama asíntota horizontal.
Ejemplo 1
Encuentra una asíntota horizontal para la función.
\[ \large f(x) = \frac{x^2}{x^2+1} \]Respuesta:
Para encontrar la asíntota horizontal, necesitamos encontrar el límite de la función \(f(x)\) cuando \(x\) se acerca al infinito. Si no está familiarizado con el cálculo, primero debe intentar evaluar la función con un valor muy grande de \(x\).
Por ejemplo, digamos que \(x = 1,000,000\). Insertemos este número en la función:
\[ \large f(1,000,000) = \frac{1,000,000^2}{1,000,000^2+1} = \frac{1,000,000,000,000}{1,000,000,000,000+1}\] \[ = \frac{1,000,000,000,000}{1,000,000,000,001} = 0.999999999999 \]que está muy cerca de 1. Entonces uno debería sospechar que el límite es 1. De hecho, resulta que cuando \(x\) es grande, el valor de \(x^2\) es tan grande con respecto a 1, que \(x^2\) es muy similar a \(x^2 + 1\) al menos en términos relativos. Entonces tenemos, dividiendo el numerador y el denominador por \(x^2\):
\[ \large f(x) = \frac{x^2}{x^2+1} = \frac{1}{1+\frac{1}{x^2}} \rightarrow \frac{1}{1+0} = 1 \]porque \(\frac{1}{x^2}\) se acerca a 0 cuando \(x\) se acerca al infinito. Por lo tanto, no es difícil demostrar o convencerse de que
\[\large \lim_{x\to\infty} f(x) =\large \lim_{x\to\infty} \frac{x^2}{x^2+1} = 1\]lo que significa que la asíntota horizontal es \(y = 1\). Ahora bien, ten cuidado con tu respuesta si estás respondiendo un examen o una tarea. Algunas personas dirán "la asíntota horizontal es 1", lo cual es incorrecto.
Técnicamente, la asíntota horizontal es la función \(y = 1\), y NO el número 1. La asíntota horizontal es una función constante, que no es lo mismo que un número. Solo lo digo, porque hay algunos estudiantes quisquillosos por ahí.
Ejemplo 2
Encuentre una asíntota horizontal, si existe para la función.
\[ \large f(x) = \frac{x^3}{x^2+1} \]Respuesta:
Dividiendo numerador y denominador por \(x^2\):
\[ \large f(x) = \frac{x}{1+\frac{1}{x^2}} \]¡Pero espera! ¿El truco no funcionó aquí? Sí lo hizo. Observe que el denominador se acercará mucho a 1 a medida que \(x\) se haga muy grande, y el numerador se volverá muy grande.
No es difícil creer que \(f(x)\) converge al infinito, por lo que no existe una asíntota horizontal. Cada vez que veamos una función ilimitada, como es el caso de \(f(x)\) en este ejemplo, no tendremos una asíntota horizontal.
¿asíntota horizontal o asíntotas horizontales?
Técnicamente podría haber dos asíntotas horizontales, una a la izquierda y otra a la derecha. La asíntota horizontal izquierda es \(y = h_L\) si
\[\large \lim_{x \to -\infty} f(x) = h_L\]De manera similar, la asíntota horizontal derecha es \(y = h_R\) si
\[\large \lim_{x \to +\infty} f(x) = h_R\]en caso de que alguno de los límites anteriores exista y sea finito. Puede suceder que una función tenga dos asíntotas horizontales, tenga una sola asíntota horizontal o no tenga ninguna.
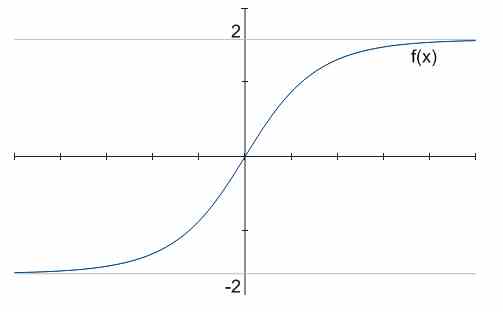
Por ejemplo, en el gráfico anterior, hay dos asíntotas horizontales, \(y = -2\) y \(y = 2\).
¿cuál es la regla para encontrar la asíntota horizontal?
No existen reglas generales que funcionen para todos los casos. En el caso general, necesitamos calcular el límite cuando \(x\) se acerca a \(-\infty\), y el límite cuando \(x\) se acerca a \(+\infty\).
Si alguno de esos límites existe y es finito, tendremos las asíntotas horizontales.
Se puede idear una regla específica para el caso de que la función dada \(f(x)\) sea el cociente de dos polinomios. Si ese es el caso, supongamos que \(m\) es el orden del polinomio en el numerador y \(n\) es el orden del polinomio en el denominador. Entonces tenemos los siguientes casos:
Caso 1: Si \(m < n\), entonces la asíntota horizontal es \(y = 0\).
Caso 2: Si \(m = n\) y \(a\) es el coeficiente principal del polinomio en el numerador y \(b\) es el coeficiente principal del polinomio en el denominador, entonces la asíntota horizontal es \(\displaystyle y = \frac{a}{b}\).
Caso 3: Si \(m > n\), entonces no hay asíntota horizontal.
Ejemplo 2
Encuentre, si existe, la asíntota horizontal de la función.
\[\large f(x) = \frac{3x^2+2x-1}{2x^2 -x+2}\]Respuesta:
La función consta del cociente de dos polinomios. El polinomio en el numerador es \(3x^2+2x-1\), que es un polinomio de orden 2, entonces \(m = 2\) y coeficientes principales 3.
El polinomio en el denominador es \(2x^2 -x+2\), que es un polinomio de orden 2, entonces \(n = 2\), y la constante principal 2. Puedes usar nuestro Calculadora de polinomios para realizar esta división mostrando todos los pasos.
Por lo tanto, dado que en este caso \(m = n\), hay una asíntota horizontal y es el cociente de los coeficientes principales, entonces, en este caso, la asíntota horizontal es
\[\large y = \frac{3}{2}\]Más sobre asíntotas horizontales
Entonces tu pregunta es cómo encontrar asíntotas de una ecuación, ¿verdad? En primer lugar, encuentras asíntotas de un función , no de una ecuación. Luego, es necesario comenzar con la definición general, utilizando límites.
Si no sabes cálculo y no sabes cómo calcular límites, entonces al menos deberías intentar conectar valores muy grandes de \(x\), y también valores muy negativos de \(x\) en la función, y ver cómo se comporta la función.
Incluso trazar la función con algún software puede darle una pista clara si hay asíntotas horizontales.
En última instancia, en el caso muy restringido en el que la función es una cociente de polinomios , luego podrás aplicar la regla basada en los pedidos \(m\) y \(n\).
¿cómo encontrar asíntotas horizontales con diferentes grados?
Esos son diferentes tipos de asíntotas y se llaman asíntota inclinada. Hablaremos de asíntotas inclinadas en otro tutorial.
