Was ist die Quadratwurzel von 64?
Manchmal hat eine einfache Frage wie die Quadratwurzel von 64 eine Antwort, die einige verwirren kann. In diesem Fall werden wir einige Mythen zerstreuen.
Das Hauptziel dieses Tutorials ist es, ein paar Dinge über Quadratwurzeln und Radikale zu lernen, damit Sie ohne zu zögern Fragen dazu beantworten können.
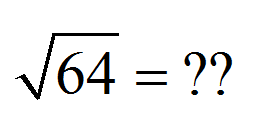
Das Erste ist das Erste. Lassen Sie uns die Definition der Quadratwurzel formulieren:
Die Quadratwurzel einer bestimmten Zahl ist die positiv Zahl (oder Null), so dass im Quadrat die angegebene Zahl entsteht .
Das ist es. Wenn also eine Zahl \(x\) gegeben ist, ist ihre Quadratwurzel eine Zahl \(b\), so dass \(b \ge 0\) und
\[b^2 = x\]Wenn wir uns den obigen Ausdruck ansehen, können wir sehen, dass, wenn \(b\) die Quadratwurzel von \(x\) sein wird, \(x = b^2\), und da eine Quadratzahl nicht negativ sein kann, kann \(x\) nur nicht negativ sein (wenn wir in der Lage sein wollen finde seine Quadratwurzel).
Fazit : Wir können nur Quadratwurzeln nicht negativer Werte \(x\) berechnen. Oder anders gesagt, die Domäne der Funktion \(\sqrt x\) ist \([0,+\infty)\).
Beantworten Sie also unsere erste Frage:
Was ist die Quadratwurzel von 64?
Basierend auf dem, was wir definiert haben, müssen wir einen nicht negativen Wert \(b\) finden, damit \(b^2 = 64\). Gibt es eine Zahl, die diese Eigenschaften erfüllt?
Ja, was wäre, wenn wir es mit \(b = 8\) versuchen würden? Ok, also \(b = 8\) ist nicht negativ und \(b^2 = 8^2 = 64\).
Wir haben also die Quadratwurzel von 64 gefunden, die 8 ist, weil 8 nicht negativ ist, und \(8^2 = 64\). Wir schreiben dies als:
\[ \sqrt{64} = 8 \]Der Mythos über die Quadratwurzelfunktion
Nun gehen wir zu dem Thema, das dieses Tutorial motiviert hat ... Die obige Definition der Quadratwurzel ermöglicht es uns, die allgemeine Aussage zu verwerfen, dass "die Quadratwurzel von 64 plus oder minus 8 ist", was falsch ist. Tatsächlich
\[\sqrt{64} =\not \pm 8\]Jetzt können wir verstehen, warum solch ein Mythos weitergeht. In der Tat haben sowohl 8 als auch -8 die Eigenschaft \(8^2 = 64\) und \((-8)^2 = 64\). Warum ist -8 dann NICHT die Quadratwurzel von 64?
Denn per Definition haben wir gesagt, dass die Quadratwurzel die nicht negative Zahl sein muss, die die Eigenschaft hat, dass sie im Quadrat der angegebenen Zahl entspricht. Und -8 verfehlt die Bedingung, nicht negativ zu sein.
Der Graph der Quadratwurzelfunktion
Schauen Sie sich das Diagramm der Quadratwurzelfunktion unten an:
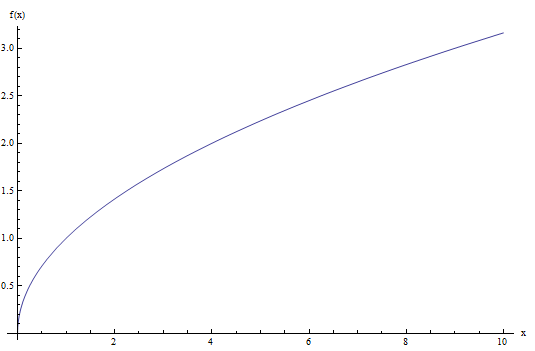
Wie Sie sehen können, nimmt diese Funktion nur nicht negative Werte an und besteht tatsächlich den vertikalen Linientest, sodass es sich um eine Funktion handelt.
Am Ende macht die Definition der Quadratwurzel als nicht negatives \(b\), so dass \(b^2 = x\) die Quadratwurzel zu einer Funktion macht.
Wenn wir tatsächlich \(\sqrt{64} = \pm 8\) hätten, wäre \(\sqrt x\) keine Funktion, sondern eine Beziehung, da die vertikale Linie bei \(x = 64\) den Graphen zweimal kreuzen würde (bei 8 und -8).
Was ist mit anderen radikalen Funktionen?
Es gibt andere Arten radikaler Funktionen. Zum Beispiel die Kubikwurzel \(\sqrt[3] x\). In diesem Fall muss keine Regel für die Auswahl des Radikals festgelegt werden, da die Kubikwurzel einer bestimmten Zahl \(x\) die Zahl \(b\) ist, sodass \(b^3 = x\).
Kubikwurzel
Für den Kubikwurzelfall müssen keine Unterscheidungen getroffen werden, da für ein bestimmtes \(x\) nur EINE Nummer \(b\) vorhanden ist, sodass \(b^3 = x\).
Beispielsweise
\[\sqrt[3]{64} = 4\]einfach weil \(4^3 = 64\). Oder
\[\sqrt[3]{-64} = -4\]einfach weil \((-4)^3 = -64\). Dies bedeutet, dass es keine Mehrdeutigkeit wie im Fall der Quadratwurzel gibt.
Quarzwurzel
Für den Fall der Quartic Root ist es der Quadratwurzel ähnlich. Wir werden das \(\sqrt[4] x = b\) haben, wenn \(b \ge 0\) und \(b^4 = x\).
Beispielsweise
\[\sqrt[4]{16} = 2\]weil \(2^4 = 16\) und \(2 \ge 0\). Aber
\[\sqrt[4]{16} =\not -2\]denn obwohl \((-2)^4 = -16\), haben wir das \(-2 < 0\), so dass dann die Nicht-Negativitätsbedingung nicht erfüllt ist.
Wie wäre es mit der n-ten Wurzel \(\sqrt[n] x\) im Allgemeinen ???.
Ich bin sicher, Sie haben es erraten.
Für \(n\) ist die Situation wie bei der Quadratwurzel: \(\sqrt[n] x = b\) wenn \(b \ge 0\) und \(b^n = x\).
Für \(n\) ungerade ist die Situation wie die Quadratwurzel: \(\sqrt[n] x = b\) wenn \(b^n = x\).
Mehr zur Berechnung der Quadratwurzel
Eine Sache, auf die wir Wert gelegt haben, war, dass die Quadratwurzelfunktion \(\sqrt x\) ein nicht negatives Argument \(x\) annehmen muss, wenn wir die Quadratwurzel berechnen wollen.
Wir haben dort ein wenig geschummelt, weil wir nicht den ganzen Satz geschrieben haben: Die Quadratwurzelfunktion \(\sqrt x\) muss ein nicht negatives Argument \(x\) annehmen, wenn wir die Quadratwurzel in der REAL LINE berechnen wollen.
ABER wenn \(x < 0\), dh wenn \(x\) negativ ist, dann ist \(\sqrt x\) immer noch definiert, jedoch nicht als reelle Zahl, sondern als komplexe Zahl.
Die Grundeinheit der komplexen Quadratwurzel ist die Quadratwurzel von -1. Was ist \(\sqrt{-1}\)???
Geben Sie die komplexen Zahlen ein: Es gibt eine komplexe Zahl namens \(i\), damit
\[\sqrt{-1} = i \]Ab diesem Zeitpunkt funktionieren die Eigenschaften der Quadratwurzel gleich. Beispielsweise:
\[\sqrt{-4} = \sqrt{4} \sqrt{-1} = 2\sqrt{-1} = 2i \]