Ein Gleichungssystem ist einfach ein Satz von zwei oder mehr gleichzeitigen Gleichungen, die gelöst werden müssen. Normalerweise haben Sie die gleiche Anzahl von Gleichungen und Unbekannten (Variablen), dies muss jedoch nicht der Fall sein.

Das einzige, was klar ist, ist, dass Sie ZWEI oder MEHR Gleichungen gleichzeitig haben müssen, um ein Gleichungssystem zu haben. Zum Beispiel das folgende System

ist ein Gleichungssystem mit zwei Gleichungen und zwei Unbekannten (\(x\) und \(y\)). Oder zum Beispiel das folgende System:

ist ein Gleichungssystem mit zwei Gleichungen und drei Unbekannten (\(x\), \(y\) und \(z\)).

Das erste Beispiel ist ein Beispiel für ein lineares Gleichungssystem.

Das zweite Beispiel ist ein Beispiel für ein System nichtlinearer Gleichungen. Warum? Sie haben es erraten: Der Ausdruck \(z^2\) in der ersten Gleichung macht es nichtlinear.

Im Allgemeinen hängt die Strategie zur Lösung eines Gleichungssystems davon ab, ob es linear ist oder nicht. Für lineare Gleichungssysteme gibt es systematische Methoden, um sie zu lösen, wie z Cramers Regel . Für nichtlineare Gleichungssysteme gibt es keine feste Strategie, und wir müssen von Fall zu Fall gehen.

Anzahl der Lösungen eines Gleichungssystems

Wie viele Lösungen hat ein Gleichungssystem, wenn überhaupt? Eine allgemeine Antwort auf diese Frage kann nur bei linearen Gleichungssystemen gegeben werden, die auf der Beziehung zwischen der Anzahl der Gleichungen und der Anzahl der Unbekannten beruhen.

Typischerweise kann es in einem System linearer Gleichungen, in dem die Anzahl der Gleichungen gleich oder größer als die Anzahl der Unbekannten ist, eine eindeutige Lösung geben, keine Lösung oder unendliche Lösungen.

Wenn die Anzahl der Gleichungen geringer ist als die Anzahl der Unbekannten, kann es unendlich viele oder gar keine Lösungen geben, aber es kann keine eindeutige Lösung geben.

Wie findet man ein Gleichungssystem?

Diese Frage bezieht sich darauf, wie man zu einem Gleichungssystem kommt. Es gibt verschiedene Kontexte. Beispielsweise haben Sie es möglicherweise mit einem Wortproblem zu tun, bei dem Sie drei verschiedene Arten von Lebensmitteln herstellen, und Sie haben verschiedene Arten von Einschränkungen für diese Lebensmittel in Bezug auf Kosten, Kalorien usw. Jede dieser Einschränkungen kann wahrscheinlich sein als Gleichung dargestellt.

Es gibt unzählige Anwendungen, bei denen unterschiedliche Einschränkungen zu linearen Gleichungen führen, die gleichzeitig gelöst werden müssen, um das Problem in ein Gleichungssystem umzuwandeln.

BEISPIEL 1

Beispiel für ein Gleichungssystem: Ist das folgende Gleichungssystem linear oder nichtlinear?

ANTWORTEN:

Zuallererst ist das Obige ein Gleichungssystem mit drei Gleichungen und drei Unbekannten (\(x\), \(y\) und \(z\)). Die ersten beiden Gleichungen sind aufgrund des Ausdrucks \(\sin(z)\) linear, unabhängig davon, ob die letzte Gleichung nicht linear ist. Um eine lineare Gleichung zu haben, müssen die Unbekannten nur mit einer Konstanten multipliziert werden.

Das obige Gleichungssystem ist also nicht linear, selbst wenn die ersten beiden Gleichungen linear sind, ist die dritte nicht linear. Für ein System reicht es aus, eine Gleichung zu haben, um nicht linear zu sein, damit das gesamte System nicht linear ist.

BEISPIEL 2

Angenommen, Sie stellen drei Arten von Hemden in den folgenden Mengen her: \(x\), \(y\) und \(z\). Typ 1 kostet 1 USD, Typ 2 1,2 USD und Typ 3 1,5 USD. Die Herstellung von Typ 1 dauert 1 Stunde, die Herstellung von Typ 2 0,5 Stunden und die Herstellung von Typ 3 0,8 Stunden.

Ich weiß, dass ich 800 Dollar ausgeben muss und 500 Stunden zur Verfügung stehen. Basierend auf meinen Bedarfsschätzungen möchte ich außerdem insgesamt Hemden vom Typ 1 produzieren, die der kombinierten Summe von Hemden vom Typ 2 und Typ 3 entsprechen.

Schreiben Sie ein Gleichungssystem, das auf diesen Einschränkungen basiert. Ist dieses System linear?

ANTWORTEN:

Beachten Sie, dass es drei Unbekannte gibt (\(x\), \(y\) und \(z\)), die der Anzahl der Hemden jedes Typs entsprechen, die hergestellt werden müssen. Außerdem haben wir drei Gleichungen: eine für die Kosten, eine für die Anzahl der verfügbaren Stunden und eine für die Beschränkung der Anzahl der Typ-1-Hemden und der anderen Typen.

Die folgenden Gleichungen repräsentieren die Situation:

Unter Verwendung der Konvention, alle Begriffe, die von den Unbekannten abhängen, auf der linken Seite zu belassen, schreiben wir die letzte Gleichung neu, um Folgendes zu erhalten:

Beachten Sie, dass jede Gleichung linear ist. Das System ist also ein System linearer Gleichungen.

Wie lösen Sie Gleichstellungssysteme im Allgemeinen?

Wie oben erwähnt, gibt es keine einzige Strategie, die für alle Fälle geeignet wäre. Nur bei linearen Gleichungssystemen gibt es eine klare, klar definierte Strategie.

Dennoch gibt es einige bewährte Methoden oder Schritte, die Sie befolgen müssen, um alle Arten von Gleichungssystemen zu lösen:

Schritt 1: Identifizieren Sie jede Gleichung im System

Schritt 2: Verschieben Sie auf einer Seite der Gleichung alle Terme, die von den Unbekannten abhängen (normalerweise auf der linken Seite), und die Konstanten auf der anderen Seite

Schritt 3: Vereinfachen Sie sowohl die linke Seite (mit den Unbekannten) als auch die rechte Seite (mit den Konstanten).

Schritt 4: Identifizieren Sie die Struktur der Gleichungen. Sind die Gleichungen linear oder nicht linear?

Schritt 5: Wenn alle Gleichungen linear sind, verwenden Sie eine der systematischen Methoden zum Lösen linearer Systeme (Cramer-Regel, Substitution, Eliminierung, Gauß-Reduktion usw.).

Schritt 6: Wenn mindestens eine Gleichung nicht linear ist, können Sie versuchen, den Substitutionsansatz zu verwenden, beginnend mit der einfachsten Gleichung.

Weitere Informationen zu Gleichungssystemen

Gleichungssysteme erscheinen überall in der Mathematik, in allen Fächern. Die Fähigkeit, Gleichungssysteme systematisch zu lösen, wird sich als eine entscheidende Fähigkeit erweisen, die man beherrschen muss.

Das typischste System, das Sie finden, ist ein System linearer Gleichungen. Und häufig finden Sie lineare Gleichungssysteme mit zwei Gleichungen und zwei Unbekannten. Diese Systeme werden normalerweise als 2x2-System linearer Gleichungen bezeichnet.

Diagramm der Gleichungssysteme

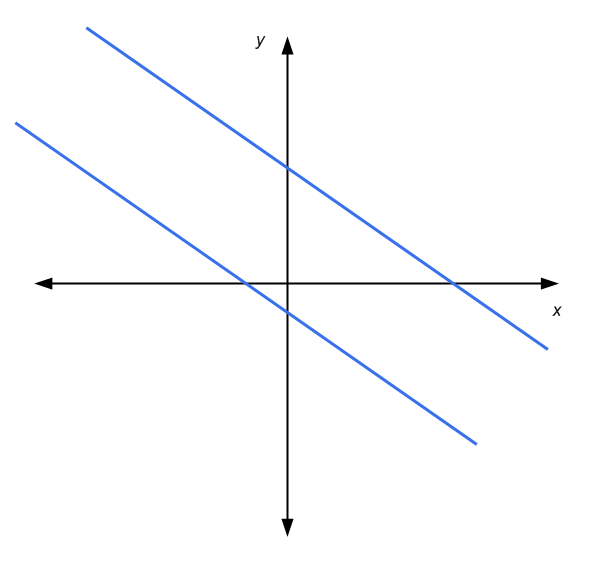
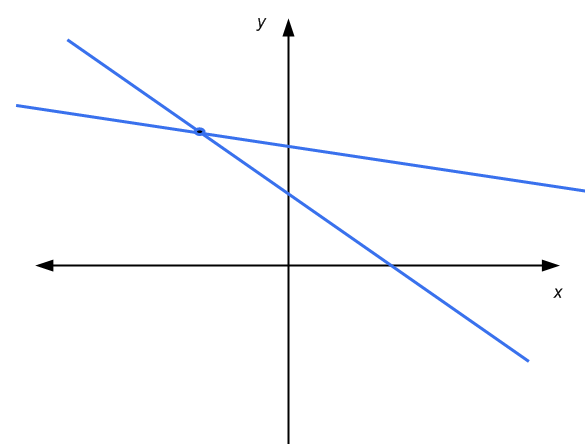
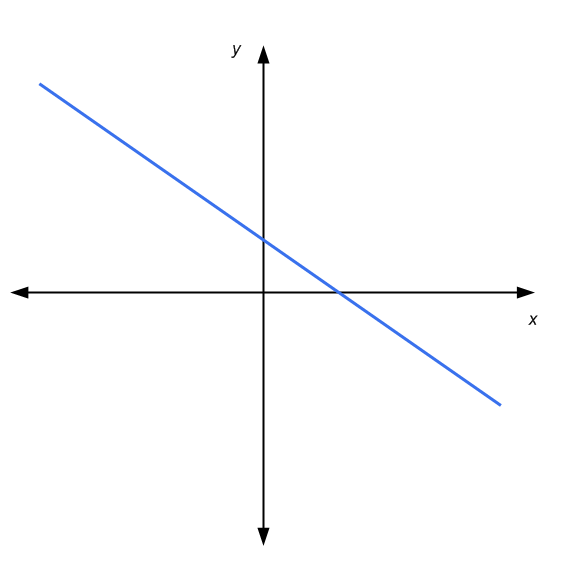
Für ein 2x2-System linearer Gleichungen haben wir den Vorteil, dass wir eine grafische Darstellung in den koordinierten Achsen verwenden können. Eine lineare Gleichung wird durch eine Linie in der x-y-Ebene dargestellt. Grafisch ist die Lösung eines 2x2-Systems der Punkt, an dem sich die beiden Linien schneiden, falls vorhanden.

In diesem Fall haben wir entweder Folgendes: Die Linien sind parallel und berühren sich nicht (keine Lösungen), die Linien schneiden sich in einem Punkt (eindeutige Lösung) oder die Linien sind parallel und berühren sich (unendlich viele Lösungen) )

Gleichungssystem Rechner

Verwenden Sie diesen Solver, wenn Sie möchten Löse ein 2x2-System linearer Gleichungen . Dieser Rechner verwendet die Cramer-Regel, um 2x2-Systeme zu lösen. Für größere Gleichungssysteme ist die beste Alternative die Verwendung von Gaußsche Eliminierungsmethode , die sich systematisch mit linearen Systemen jeder Größe befasst.