Cramers Regel
Die Cramer-Regel ist eine Technik zur systematischen Lösung linearer Gleichungssysteme auf der Grundlage von Determinantenberechnungen.
In der Regel lösen lineare Gleichungssysteme kann für Systeme, die größer als 2x2 sind, unübersichtlich sein, da es viele Möglichkeiten gibt, sie zu reduzieren, wenn drei oder mehr Variablen vorhanden sind.
Die Cramer-Regel bietet eine eindeutige und systematische Möglichkeit, Lösungen für lineare Gleichungssysteme zu finden, unabhängig von der Größe des Systems.
Die Anzahl der erforderlichen Berechnungen nimmt für große Systeme zwar zu, die Vorgehensweise ist jedoch unabhängig von der Größe des Systems genau gleich.
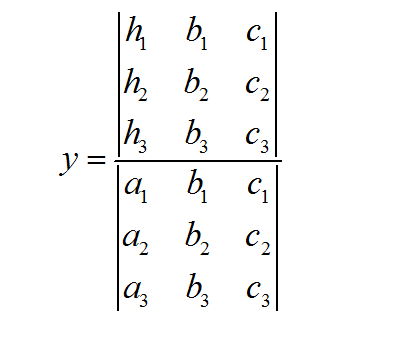
Verwendung der Cramer-Regel
Um die Sache zu vereinfachen, werden wir den Fall für \(n = 2\) ausarbeiten und dann eine allgemeinere Version erstellen, die hoffentlich sinnvoller ist, nachdem wir den Fall \(n=2\) behandelt haben.
Schritt 1
: Alle linearen 2x2-Systeme können in folgender Form geschrieben werden:
Der erste Schritt besteht also darin, diese Werte \(a_1, b_1, c_1\) und \(a_2, b_2, c_2\) für das System zu finden, das Sie lösen möchten.
Schritt 2
: Sobald Sie die Koeffizienten \(a_1, b_1, c_1\) und \(a_2, b_2, c_2\) haben, verwenden Sie die folgenden Formeln, um nach \(x\) und \(y\) zu lösen:
In der obigen Formel, in der "det" steht, bedeutet dies die Determinante der entsprechenden Matrix. Manchmal wird für Determinanten eine kompaktere Notation verwendet, wie unten gezeigt:
\[\large \displaystyle \det \left[\begin{matrix} a_1 & b_1 \\ a_2 & b_2 \end{matrix}\right] = \left|\begin{matrix} a_1 & b_1 \\ a_2 & b_2 \end{matrix}\right| \]Wenn wir also die obige Notation verwenden, erhalten wir diese kompakteren Formeln für die Cramer-Regel:
\[\large \displaystyle x = \frac{ \left|\begin{matrix} c_1 & b_1 \\ c_2 & b_2 \end{matrix}\right| }{\left|\begin{matrix} a_1 & b_1 \\ a_2 & b_2 \end{matrix}\right|} \] \[\large \displaystyle y = \frac{ \left|\begin{matrix} a_1 & c_1 \\ a_2 & c_2 \end{matrix}\right| }{\left|\begin{matrix} a_1 & b_1 \\ a_2 & b_2 \end{matrix}\right|} \]Lassen Sie uns visuell verstehen, was passiert. Beachten Sie, dass sowohl \(x\) als auch \(y\) im Nenner dieselbe Determinante haben.
Die Koeffizienten dieser gemeinsamen Matrix, die im Nenner verwendet werden, werden direkt von den Koeffizienten abgeleitet, die \(x\) und \(y\) im System multiplizieren. Siehe das Bild unten:
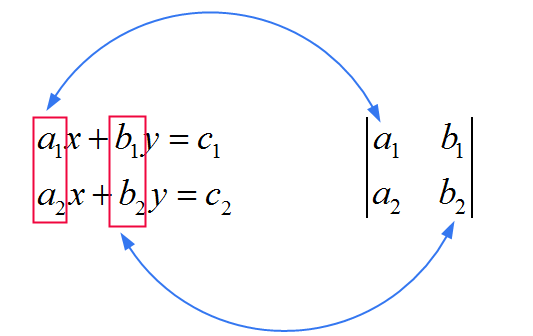
Jetzt sehen wir, dass \(x\) und \(y\) sich darin unterscheiden, was sie im Zähler haben. Denken Sie daran, um sich an die Regel zu erinnern:
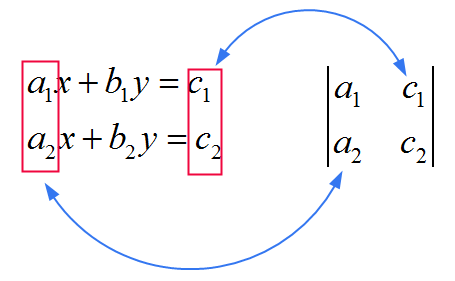
Für \(x\) verwenden Sie die gleiche Matrix als die im Nenner, nur dass Sie die ERSTE Spalte durch die Koeffizienten \(c_1\) und \(c_2\) ersetzen. Siehe das Bild unten
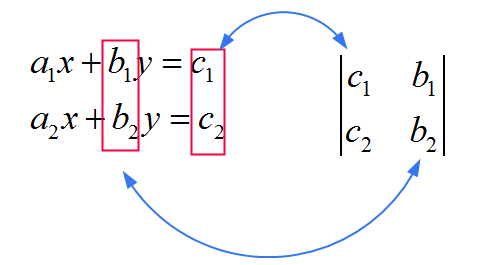
Für \(y\) verwenden Sie die gleiche Matrix als die im Nenner, nur dass Sie die zweite Spalte durch die Koeffizienten \(c_1\) und \(c_2\) ersetzen. Siehe das Bild unten
BEISPIEL 1
Lösen Sie das folgende 2x2-Linearsystem:
\[\large 2x + 8y = 10\] \[\large 2x - 4y = 4\]ANTWORTEN:
Befolgen wir die beiden oben beschriebenen Schritte, um die Cramer-Regel zur Lösung des obigen Systems zu verwenden:
Schritt 1
: Wir müssen die Koeffizienten für die entsprechenden Determinanten identifizieren.
Für die Matrix im Nenner verwenden wir
\[ \left|\begin{matrix} a_1 & b_1 \\ a_2 & b_2 \end{matrix}\right| = \left|\begin{matrix} 2 & 8 \\ 2 & -4 \end{matrix}\right| \]In diesem Fall \(c_1 = 10, c_2 = 4\) ersetzen wir für die Determinante, die zur Berechnung von \(x\) verwendet wird, die vorherige Matrix durch Ändern der Spalte FIRST:
\[ \left|\begin{matrix} c_1 & b_1 \\ c_2 & b_2 \end{matrix}\right| = \left|\begin{matrix} 10 & 8 \\ 4 & -4 \end{matrix}\right| \]Für die Determinante, die zur Berechnung von \(y\) verwendet wird, ersetzen wir die vorherige Matrix durch Ändern der zweiten Spalte:
\[ \left|\begin{matrix} a_1 & c_1 \\ a_2 & c_2 \end{matrix}\right| = \left|\begin{matrix} 2 & 10 \\ 2 & 4 \end{matrix}\right| \]Jetzt haben wir die Lösung:
\[\large \displaystyle x = \frac{ \left|\begin{matrix} c_1 & b_1 \\ c_2 & b_2 \end{matrix}\right| }{\left|\begin{matrix} a_1 & b_1 \\ a_2 & b_2 \end{matrix}\right|} \] \[ = \frac{\left|\begin{matrix} 10 & 8 \\ 4 & -4 \end{matrix}\right|}{\left|\begin{matrix} 2 & 8 \\ 2 & -4 \end{matrix}\right|} = \frac{10 \times (-4) - 4\times 8}{2 \times (-4) - 2 \times 8} = \frac{-72}{-24} = 3 \]und für \(y\):
\[\large \displaystyle y = \frac{ \left|\begin{matrix} a_1 & c_1 \\ a_2 & c_2 \end{matrix}\right| }{\left|\begin{matrix} a_1 & b_1 \\ a_2 & b_2 \end{matrix}\right|} \] \[ = \frac{\left|\begin{matrix} 2 & 10 \\ 2 & 4 \end{matrix}\right|}{\left|\begin{matrix} 2 & 8 \\ 2 & -4 \end{matrix}\right|} = \frac{2 \times 4 - 2\times 10}{2 \times (-4) - 2 \times 8} = \frac{-12}{-24} = \frac{1}{2} \]Daher lautet die Lösung \(x = 3\), \(y = 1/2\).
Cramers Regel für den allgemeinen Fall
Das Schöne an Cramers Regel ist, dass sie genau das gleiche Verfahren anwendet, egal ob es sich um ein 2x2-System oder um ein 10x10-System handelt. Das Konzept ist das gleiche.
Nehmen wir also an, dass \(x_1, x_2, ..., x_n\) die Variablen (die Unbekannten) sind, und wir wollen das folgende n x n-System linearer Gleichungen lösen:
\[\large a_{11} x_1 + a_{12} x_2 + .... + a_{1n} x_n = c_1 \] \[\large a_{21} x_1 + a_{22} x_2 + .... + a_{2n} x_n = c_2 \] \[\large \vdots \] \[\large a_{n1} x_1 + a_{n2} x_2 + .... + a_{nn} x_n = c_n \]Um nach \(x_1, x_2, ..., x_n\) zu lösen, verwenden wir die folgende Determinante für den Nenner:
\[\large\displaystyle \left|\begin{matrix} a_{11} & a_{12} & ... & a_{1n} \\ a_{21} & a_{22} & ... & a_{2n} \\ \vdots & \vdots & ... & \vdots\\ a_{n1} & a_{n2} & ... & a_{nn}\end{matrix}\right|\]• Die Lösung für \(x_1\) lautet
\[\large\displaystyle x_1 = \frac{ \left|\begin{matrix} c_1 & a_{12} & ... & a_{1n} \\ c_2 & a_{22} & ... & a_{2n} \\ \vdots & \vdots & ... & \vdots\\ c_n & a_{n2} & ... & a_{nn}\end{matrix}\right| }{\left|\begin{matrix} a_{11} & a_{12} & ... & a_{1n} \\ a_{21} & a_{22} & ... & a_{2n} \\ \vdots & \vdots & ... & \vdots\\ a_{n1} & a_{n2} & ... & a_{nn}\end{matrix}\right|} \]• Die Lösung für \(x_2\) lautet
\[\large\displaystyle x_1 = \frac{ \left|\begin{matrix} a_{11} & c_1 & ... & a_{1n} \\ a_{21} & c_2 & ... & a_{2n} \\ \vdots & \vdots & ... & \vdots\\ a_{n1} & a_{n2} & ... & c_n \end{matrix}\right| }{\left|\begin{matrix} a_{11} & a_{12} & ... & a_{1n} \\ a_{21} & a_{22} & ... & a_{2n} \\ \vdots & \vdots & ... & \vdots\\ a_{n1} & a_{n2} & ... & a_{nn}\end{matrix}\right|} \]Und so weiter. Wie Sie sehen können, ist die Determinante im Nenner dieselbe, und die im Zähler wird erhalten, indem die erste Spalte mit \((c_1, ..., c_n)\) für \(x_1\) geändert wird. Für \(x_2\) ändern wir die zweite Spalte durch \((c_1, ..., c_n)\), für \(x_3\) ändern wir die dritte Spalte und so weiter. Du hast die Idee.
BEISPIEL 2
Lösen Sie das folgende System von 3x3 linearen Gleichungen mit der Cramer-Regel.
\[\large x_1 + x_2 + x3 = 20\] \[\large x_1 - x_2 + x3 = 4\] \[\large 2x_1 + x_2 - x3 = 16\]ANTWORTEN:
Zunächst identifizieren wir die Determinante, die in den Nenner geht:
\[\large\displaystyle \left|\begin{matrix} 1 & 1 & 1 \\ 1 & -1 & 1 \\ 2 & 1 & -1 \end{matrix}\right|\]Außerdem müssen wir den Vektor der \(c_i\) -Koeffizienten identifizieren:
\[\large\displaystyle \left[\begin{matrix} 20 \\ 4 \\ 16 \end{matrix}\right]\]Dieser Vektor ersetzt die entsprechenden Spalten der gemeinsamen Determinante vom Nenner. Wir bekommen:
\[\large\displaystyle x_1 = \frac{ \left|\begin{matrix} 20 & 1 & 1 \\ 4 & -1 & 1 \\ 16 & 1 & -1 \end{matrix}\right| }{ \left|\begin{matrix} 1 & 1 & 1 \\ 1 & -1 & 1 \\ 2 & 1 & -1 \end{matrix}\right| } = \frac{40}{6} = \frac{20}{3}\] \[\large\displaystyle x_2 = \frac{ \left|\begin{matrix} 1 & 20 & 1 \\ 1 & 4 & 1 \\ 2 & 16 & -1 \end{matrix}\right| }{ \left|\begin{matrix} 1 & 1 & 1 \\ 1 & -1 & 1 \\ 2 & 1 & -1 \end{matrix}\right| } = \frac{40}{6} = \frac{20}{3}\] \[\large\displaystyle x_3 = \frac{ \left|\begin{matrix} 1 & 1 & 20 \\ 1 & -1 & 4 \\ 2 & 1 & 16 \end{matrix}\right| }{ \left|\begin{matrix} 1 & 1 & 1 \\ 1 & -1 & 1 \\ 2 & 1 & -1 \end{matrix}\right| } = \frac{40}{6} = \frac{20}{3}\]Mehr über Cramers Regel
Die Cramer-Regel spielt eine besondere Rolle bei der effizienten Lösung linearer Gleichungssysteme. Es beinhaltet die Verwendung von Determinanten, um eine Aufgabe sehr einfach zu machen, die sonst wirklich kompliziert wäre, insbesondere für größere Systeme.
Letztendlich, um lineare Systeme lösen Alles, was Sie tun müssen, ist, eine Zahlenmatrix-Determinante basierend auf dem zu lösenden System zu identifizieren und eine einfache algebraische Operation durchzuführen, um das System zu lösen.
Anwendungen
Die Cramer-Regel hat viele Anwendungen sowohl in der linearen Algebra als auch in den Differentialgleichungen.