Horizontale asymptoten
In diesem Tutorium werden wir das Konzept der horizontale Asymptote und ihre wichtigsten Anwendungen. Wir werden versuchen, allzu technische Erklärungen zu vermeiden, aber ein paar Anspielungen auf die Infinitesimalrechnung werden vorkommen.
Das Wichtigste, was man aus diesem Tutorial mitnehmen kann, ist eine starke geometrische Intuition für horizontale Asymptoten. Lasst uns beginnen!
Was ist eine horizontale asymptote?
Eine horizontale Asymptote ist eine obere Grenze, die man sich als horizontale Linie vorstellen kann, die eine Grenze für das Verhalten des Graphen einer bestimmten Funktion setzt.
Das bedeutet, dass sich der Graph der Funktion \(f(x)\) dieser horizontalen Linie annähert, wenn der Wert von \(x\) steigt.
Wie findet man die horizontale asymptote?
Das Verständnis dieses begrenzenden horizontalen Verhaltens von Funktionen, die diese Eigenschaft aufweisen, kann sich als sehr nützlich erweisen, um horizontale Asymptoten zu finden.
Unter bestimmten Umständen sieht dieses begrenzende Verhalten für große Werte von \(x\) tatsächlich wie eine horizontale Linie aus. Siehe zum Beispiel die folgende Funktion.
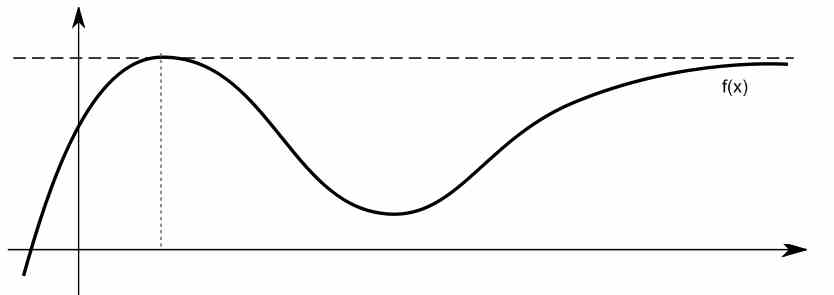
Wie findet man die horizontale asymptote einer funktion mithilfe von grenzwerten?
Um die Definition zu verdeutlichen, ist eine horizontale Linie \(y = h\) eine horizontale Asymptote der Funktion \(f(x)\), wenn
\[\large \lim_{x\to\infty} f(x) = h\]wenn der obige Grenzwert existiert und endlich ist. Für diejenigen, die noch keinen Kalkülkurs besucht haben: Die horizontale Linie \(y = h\) ist eine horizontale Asymptote der Funktion \(f(x)\), wenn \(h\) die grenze von \(f(x)\), wenn \(x\) sich der Unendlichkeit nähert. Was bedeutet es, ein "Grenzwert" zu sein? Es bedeutet, dass für hinreichend große Werte von \(x\) der Wert von \(f(x)\) so nahe an \(h\) liegt, wie wir es vorausbestimmen. Schick, nicht wahr?
Wie lautet die formel für die horizontale asymptote?
Um die Formel für die horizontale Asymptote zu finden, müssen wir zunächst den entsprechenden Grenzwert finden. Angenommen, Sie haben
\[\large \lim_{x\to\infty} f(x) = h\]In diesem Fall sagen wir, dass die horizontale Asymptote \(h\) ist, und die Formel für die horizontale Asymptote lautet \(y = h\). Mit anderen Worten, die horizontale Asymptote ist einfach eine horizontale Linie, also eine Linie mit der Steigung Null.
Damit ist klar, was eine horizontale Asymptote in Bezug auf Grenzwerte bedeutet: Der gefundene Grenzwert entspricht der Definition der horizontalen Linie, die als horizontale Asymptote bezeichnet wird.
Beispiel 1
Finden Sie eine horizontale Asymptote für die Funktion
\[ \large f(x) = \frac{x^2}{x^2+1} \]Antworten:
Um die horizontale Asymptote zu finden, müssen wir den Grenzwert der Funktion \(f(x)\) finden, wenn \(x\) sich dem Unendlichen nähert. Wenn Sie mit der Infinitesimalrechnung nicht vertraut sind, sollten Sie zunächst versuchen, die Funktion bei einem sehr großen Wert von \(x\) auszuwerten.
Nehmen wir zum Beispiel an, dass \(x = 1,000,000\). Wir setzen diese Zahl in die Funktion ein:
\[ \large f(1,000,000) = \frac{1,000,000^2}{1,000,000^2+1} = \frac{1,000,000,000,000}{1,000,000,000,000+1}\] \[ = \frac{1,000,000,000,000}{1,000,000,000,001} = 0.999999999999 \]tatsächlich stellt sich heraus, dass, wenn \(x\) groß ist, der Wert von \(x^2\) im Verhältnis zu 1 so groß ist, dass \(x^2\) zumindest relativ gesehen \(x^2 + 1\) sehr ähnlich ist. Wir haben also, wenn wir Zähler und Nenner durch \(x^2\) dividieren:
\[ \large f(x) = \frac{x^2}{x^2+1} = \frac{1}{1+\frac{1}{x^2}} \rightarrow \frac{1}{1+0} = 1 \]weil \(\frac{1}{x^2}\) sich 0 nähert, wenn \(x\) sich der Unendlichkeit nähert. Daher ist es nicht schwer zu beweisen oder sich davon zu überzeugen, dass
\[\large \lim_{x\to\infty} f(x) =\large \lim_{x\to\infty} \frac{x^2}{x^2+1} = 1\]was bedeutet, dass die horizontale Asymptote \(y = 1\) ist. Seien Sie nun vorsichtig mit Ihrer Antwort, wenn Sie einen Test oder eine Hausaufgabe beantworten. Manche Leute werden sagen "die horizontale Asymptote ist 1", was falsch ist.
Technisch gesehen ist die horizontale Asymptote die Funktion \(y = 1\) und NICHT die Zahl 1. Die horizontale Asymptote ist eine Funktion, die konstant ist, was nicht dasselbe ist wie eine Zahl. Ich sage das nur, weil es da draußen einige pingelige Schüler gibt.
Beispiel 2
Finden Sie eine horizontale Asymptote, falls es sie für die Funktion gibt
\[ \large f(x) = \frac{x^3}{x^2+1} \]Antworten:
Durch Division von Zähler und Nenner durch \(x^2\):
\[ \large f(x) = \frac{x}{1+\frac{1}{x^2}} \]Aber halt! Der Trick hat hier nicht funktioniert? Doch, hat er. Beachten Sie, dass der Nenner sehr nahe an 1 herankommt, wenn \(x\) sehr groß wird, und dass der Zähler sehr groß wird.
Es ist nicht schwer zu glauben, dass \(f(x)\) gegen unendlich konvergiert, so dass es keine horizontale Asymptote gibt. Jedes Mal, wenn wir eine Funktion sehen, die unbegrenzt ist, wie es bei \(f(x)\) in diesem Beispiel der Fall ist, werden wir keine horizontale Asymptote haben.
Horizontale asymptote oder horizontale asymptoten?
Technisch gesehen könnte es zwei horizontale Asymptoten geben, eine nach links und eine nach rechts. Die linke horizontale Asymptote ist \(y = h_L\), wenn
\[\large \lim_{x \to -\infty} f(x) = h_L\]In ähnlicher Weise ist die rechte horizontale Asymptote \(y = h_R\), wenn
\[\large \lim_{x \to +\infty} f(x) = h_R\]für den Fall, dass einer der oben genannten Grenzwerte existiert und endlich ist. Es kann vorkommen, dass eine Funktion zwei horizontale Asymptoten hat, dass sie nur eine horizontale Asymptote hat oder dass sie keine hat.
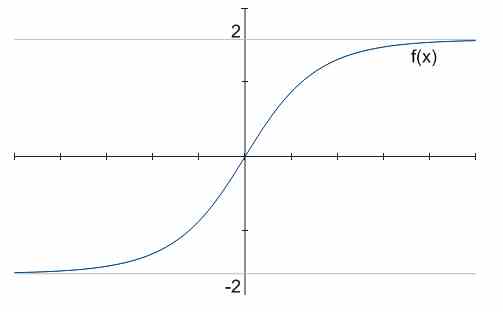
Im obigen Diagramm gibt es zum Beispiel zwei horizontale Asymptoten, \(y = -2\) und \(y = 2\).
Wie lautet die regel zur bestimmung der horizontalen asymptote?
Es gibt keine allgemeinen Regeln, die für alle Fälle gelten. Im allgemeinen Fall müssen wir den Grenzwert berechnen, wenn sich \(x\) an \(-\infty\) annähert, und den Grenzwert, wenn sich \(x\) an \(+\infty\) annähert.
Wenn eine dieser Grenzen existiert und endlich ist, haben wir die horizontalen Asymptoten.
Eine spezielle Regel lässt sich für den Fall aufstellen, dass die gegebene Funktion \(f(x)\) der Quotient zweier Polynome ist. Wenn das der Fall ist, nehmen wir an, dass \(m\) die Ordnung des Polynoms im Zähler und \(n\) die Ordnung des Polynoms im Nenner ist. Dann haben wir die folgenden Fälle:
Fall 1: Wenn \(m < n\), dann ist die horizontale Asymptote \(y = 0\).
Fall 2: Wenn \(m = n\) und \(a\) der Leitkoeffizient für das Polynom im Zähler und \(b\) der Leitkoeffizient für das Polynom im Nenner ist, dann ist die horizontale Asymptote \(\displaystyle y = \frac{a}{b}\).
Fall 3: Wenn \(m > n\), dann gibt es keine horizontale Asymptote.
Beispiel 2
Finden Sie, falls vorhanden, die horizontale Asymptote der Funktion
\[\large f(x) = \frac{3x^2+2x-1}{2x^2 -x+2}\]Antworten:
Die Funktion besteht aus dem Quotienten von zwei Polynomen. Das Polynom im Zähler ist \(3x^2+2x-1\), das ein Polynom der Ordnung 2 ist, also dann \(m = 2\), und Leitkoeffizienten 3.
Das Polynom im Nenner ist \(2x^2 -x+2\), ein Polynom der Ordnung 2, also \(n = 2\), mit der führenden Konstante 2. Sie können unsere Polynomrechner um diese Aufteilung mit allen Schritten durchzuführen.
Da es in diesem Fall \(m = n\) eine horizontale Asymptote gibt, die der Quotient der führenden Koeffizienten ist, ist die horizontale Asymptote in diesem Fall also
\[\large y = \frac{3}{2}\]Mehr über horizontale asymptoten
Ihre Frage ist also, wie man die Asymptoten einer Gleichung findet, richtig? Zunächst einmal findet man Asymptoten einer Funkwerk und nicht die einer Gleichung. Dann müssen Sie mit der allgemeinen Definition beginnen und Grenzwerte verwenden.
Wenn Sie keine Ahnung von Analysis haben und nicht wissen, wie man Grenzwerte berechnet, dann sollten Sie zumindest versuchen, sehr große Werte von \(x\) und auch sehr negative Werte von \(x\) in die Funktion einzusetzen und zu sehen, wie sich die Funktion verhält.
Sogar das Plotten der Funktion mit einer Software kann Ihnen einen klaren Hinweis darauf geben, ob es horizontale Asymptoten gibt.
In dem sehr eingeschränkten Fall, in dem die Funktion eine quotient von Polynomen dann können Sie die Regel auf der Grundlage der Aufträge \(m\) und \(n\) anwenden.
Wie findet man horizontale asymptoten mit verschiedenen graden?
Dies sind verschiedene Arten von Asymptoten, die als schräge Asymptoten bezeichnet werden. Wir werden über schräge Asymptoten in einem anderen Tutorium sprechen.
