Bogenelastizitätsformel für einen tisch

Mit der Bogenelastizitätsformel der Nachfrage können Sie die Elastizität an den in einer Nachfrageplantabelle angegebenen Punkten schätzen, ohne über eine explizite Formel für die Nachfragefunktion zu verfügen.

Sie müssen eine Tabelle mit einer Spalte für den Preis und einer Spalte für die nachgefragte Menge erstellen. Sobald Sie diese in die bereitgestellte Tabelle eingegeben oder eingefügt haben, klicken Sie auf „Berechnen“, um die entsprechenden Bogenelastizitäten berechnen zu lassen.

Beachten Sie, dass dies nur eine Annäherung ist: Die ideale Situation ist Berechnen Sie Elastizitäten mithilfe der Nachfragefunktion , durch die Verwendung von Derivaten.

Schritte zur verwendung von arc-elasticity für eine tabelle

Das Bogenelastizitätsformel Ist:

\[ \varepsilon_{ARC} = \displaystyle \left(\frac{Q_2 - Q_1}{P_2 - P_1}\right) \left(\frac{P_1 + P_2}{Q_1 + Q_2}\right)\]

Dies kann auf aufeinanderfolgende Punkte in einer Bedarfsplantabelle angewendet werden. Gehen Sie dazu folgendermaßen vor:

• Schritt 1: Bringen Sie Ihre Werte für Preis (P) und nachgefragte Menge (Q) korrekt in Tabellenform
• Schritt 2: Sie können Spalten für Q2 - Q1, P2 - P1, Q1 + Q2 und P1 + P2 erstellen, wenn Sie die Berechnungen übersichtlicher gestalten möchten, oder Sie können die Formel direkt berechnen
• Schritt 3: Es wird ein Punkt in der Tabelle übersprungen, da die Bogenelastizität einen Punkt in der Tabelle einnimmt und der Punkt, der in der Tabelle unmittelbar folgt

Mithilfe dieser Bogenelastizitätsnäherung erhalten Sie ein hervorragendes Bild der Empfindlichkeit gegenüber Preisentänderungen für das jeweilige analysierte Gut, auch wenn es sich nur um eine Näherung handelt.

Je mehr Nachfragepunkte wir haben, desto besser ist die Annäherung, insbesondere wenn die Preispunkte nahe beieinander liegen.

Was misst die lichtbogenelastizität?

Die Bogenelastizität soll eine Annäherung an die wahre Elastizität an einem bestimmten Punkt liefern. Die tatsächliche Elastizität der Nachfragekurve wird wie folgt berechnet:

\[ \varepsilon = \displaystyle \frac{dQ}{dP} \cdot \frac{P}{Q}\]

Man könnte argumentieren, dass die Bogenelastizität nur eine Annäherung ist, also welchen Wert hat sie dann? Die Antwort darauf ist, dass wir uns bei der Elastizitätsanalyse und bei der Sensitivitätsanalyse in der Wirtschaft im Allgemeinen mehr für Bereiche als für sehr spezifische Punkte interessieren.

Tatsächlich ist es für mikroökonomische Zwecke nützlich zu wissen, ob wir uns in einem unelastischen Bereich befinden oder nicht, und nicht den sehr spezifischen Wert der Elastizität

Es ist nicht so, dass der spezifische Wert nicht wichtig wäre, da es in der Tat gut ist, ihn zu haben, aber Bogenelastizitäten stellen häufig eine gute Annäherung dar und geben uns eine sehr genaue Darstellung des Elastizitätsbereichs, mit dem wir es zu tun haben.

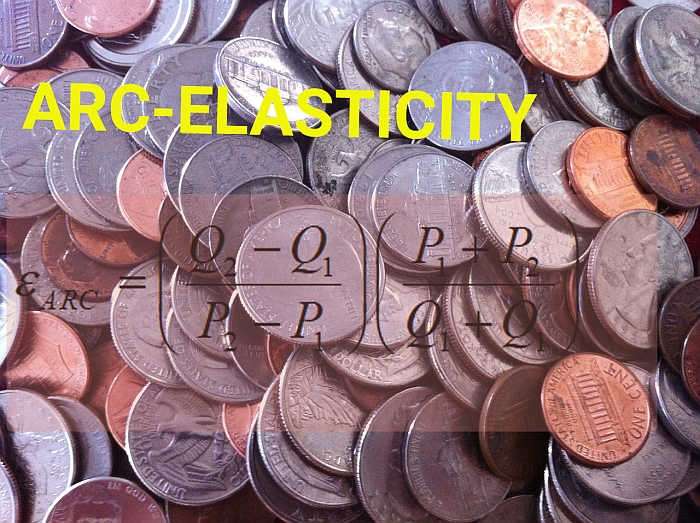
Beispiel

Betrachten Sie die folgende Nachfragetabelle mit Informationen über Preis und nachgefragte Menge

Geben Sie die Bogenelastizitätsnäherung für die Datenpunkte in dieser Tabelle an.

P	Q
1	200
1.5	190
2	170
2.5	155
3	130
3.5	110
4	90
4.5	60

Lösung: Um die Preiselastizität der Nachfrage anhand dieser Daten zu approximieren, müssen wir die folgende Bogenelastizitätsformel verwenden

\[ \varepsilon_{ARC} = \displaystyle \left(\frac{Q_2 - Q1}{P2_P1}\right)\left(\frac{P_1 + P_2}{Q_1 + Q_2}\right)\]

Indem wir die obige Formel auf alle Paare aufeinanderfolgender Datenpunkte anwenden, finden wir die folgenden Bogenelastizitäten:

P	Q	Lichtbogenelastizität
1	200	-
1.5	190	\(\left(\frac{ 190 - 200}{ 1.5 - 1}\right) \left(\frac{ 1 + 1.5}{ 200 + 190}\right) = -0.13\)
2	170	\(\left(\frac{ 170 - 190}{ 2 - 1.5}\right) \left(\frac{ 1.5 + 2}{ 190 + 170}\right) = -0.39\)
2.5	155	\(\left(\frac{ 155 - 170}{ 2.5 - 2}\right) \left(\frac{ 2 + 2.5}{ 170 + 155}\right) = -0.42\)
3	130	\(\left(\frac{ 130 - 155}{ 3 - 2.5}\right) \left(\frac{ 2.5 + 3}{ 155 + 130}\right) = -0.96\)
3.5	110	\(\left(\frac{ 110 - 130}{ 3.5 - 3}\right) \left(\frac{ 3 + 3.5}{ 130 + 110}\right) = -1.08\)
4	90	\(\left(\frac{ 90 - 110}{ 4 - 3.5}\right) \left(\frac{ 3.5 + 4}{ 110 + 90}\right) = -1.5\)
4.5	60	\(\left(\frac{ 60 - 90}{ 4.5 - 4}\right) \left(\frac{ 4 + 4.5}{ 90 + 60}\right) = -3.4\)

Interpretation

Die gefundene Tabelle zeigt die ungefähre Preiselastizität der Nachfrage für jeden der angegebenen Preispunkte. Diese Werte können ungefähr verwendet werden, um elastische und unelastische Bereiche für den angegebenen Nachfrageplan zu bestimmen.

Andere wirtschaftsrechner

Wenn Sie in der Ökonometrie arbeiten, Regressionsrechner wird wahrscheinlich nützlich sein, vor allem, weil es alle Schritte des Prozesses zeigt, Berechnung von Regressionskoeffizienten .

Sie können auch ein Log-Log-Gleichung schätzen Nachfragekurve mit konstanter Elastizität .