Como utilizar esta calculadora com passos

Esta calculadora permitir-lhe-á calcular o conceito x de uma linha, e obterá todos os passos mostrados.

O conceito x é o ponto onde a linha atravessa o eixo x, se isso alguma vez acontecer.

Em geral, há sempre um conceito x quando o declive é diferente de zero.

Quando a inclinação é zero, só haverá um "x" se a linha também cruzar a origem. As linhas verticais também têm um intercepção "x".

Como encontrar x interceptar com passos com esta calculadora

Tudo o que precisa de fazer para utilizar esta calculadora é decidir sobre uma das quatro opções fornecidas para definir a sua linha. Muitas vezes, irá fornecer a inclinação e o y-intercepção, mas também pode anotar o equação da linha directamente .

Se a equação que forneceu for válida, o solucionador passará em revista os passos necessários para identificar o conceito x, ou para indicar que não foi possível encontrar um conceito x

Conseguirá obter o conceito x a partir de uma linha em formato padrão?

Sim! de facto, utilizando o formulário padrão da linha é uma das formas mais fáceis de calcular o conceito x.

Assim, uma estratégia comum é primeiro converter a equação da linha em forma padrão e depois resolver para $x$ quando $y=0$>>.

Porque é que precisamos do conceito x?

O conceito x e Y-Intercepção de uma linha têm uma grande utilidade para dar uma intuição geométrica do comportamento numa linha nos eixos coordenados $X - Y$>>.

Exemplo do cálculo do conceito x dado uma linha

Conhece a forma padrão da linha <$\frac{3}{4} x + \frac{4}{5} y = 2$>. Encontre o conceito x da linha.

Resposta:

Foi-nos fornecida a seguinte equação:

$$\displaystyle 2x+y=y+5$$

Então, quem encontra x interceptar : Passando todas as variáveis e os seus coeficientes para a esquerda da equação, e agrupando as constantes à direita, obtemos:

$$\displaystyle 2x+\left(1-1\right)y = 5$$

e simplificando todos os termos que necessitam de simplificação, obtemos que a equação em forma normalizada é

$$\displaystyle 2x=5$$

O termo $y$ não aparece no lado esquerdo da equação, por isso podemos resolver para $x$, o que leva a

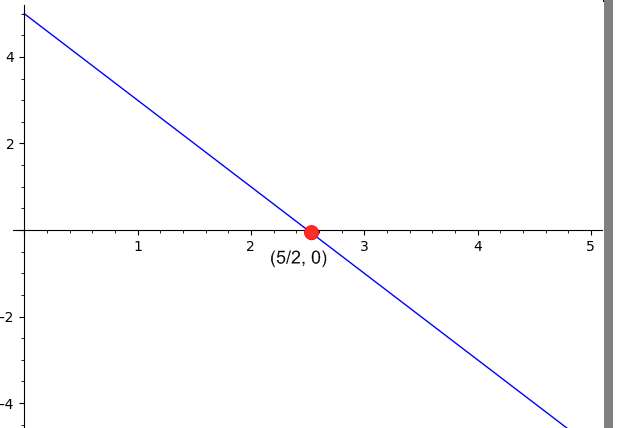
$$2 x = 5 \Rightarrow x=\frac{5}{2}$$

Observe que com base no acima exposto, isto corresponde a uma linha vertical, que vai além do valor $\displaystyle x=\frac{5}{2}$>>.

Conclusão : Com base nos dados fornecidos, concluímos que a linha atravessa o eixo x a $\displaystyle x = \frac{5}{2}$, portanto, o ponto de intercepção x correspondente é $\displaystyle \left(\frac{5}{2}, 0\right)$>>.