Solucionador de equações quadráticas

Esta calculadora permitirá que você calcular uma equação quadrática que você fornece, mostrando todas as etapas. Tudo o que você precisa fazer é fornecer uma equação quadrática válida.

Pode ser algo que já está simplificado e pronto para resolver como x^2 + 3x + 5 = 0, você pode fornecer algo que não é facilmente simplificado como 3x^2 - 4x + 5/3 = x^2 +1/3x - 1, por exemplo.

Depois de fornecer uma equação quadrática válida, tudo o que você precisa fazer é clicar em "Calcular" e você receberá todas as etapas do processo para calcular o raízes da equação quadrática que é fornecido.

Normalmente, você usará a fórmula quadrática para calcular equações quadráticas, mas essa não é a única maneira, como veremos nas seções a seguir.

Como calcular uma equação quadrática?

Existem várias estratégias para resolver equações de segundo grau. O mais comumente usado é o uso do Fórmula quadrática . Além disso, você pode resolver por completando quadrados , ou você pode resolver por fatoração quadrática .

Quais são as etapas para calcular equações quadráticas usando a fórmula quadrática?

• Passo 1: Identifique a equação quadrática que você deseja calcular
• Passo 2: Certifique-se de que a equação está totalmente simplificada, caso contrário prossiga com a simplificação, até obter uma equação da forma ax² + bx + c = 0
• Passo 3: Depois que a equação for reduzida à sua forma simplificada, você pode usar a fórmula quadrática: \(x = \displaystyle \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\)

Possivelmente, usar a fórmula da equação quadrática é a maneira mais prática de encontrar as raízes de uma equação quadrática, mas há outras razões pelas quais você usaria outros métodos.

Como resolver uma equação do segundo grau completando quadrados?

A segunda maneira mais comum de resolver uma equação quadrática é usando a técnica de completando quadrados . Não existe realmente uma fórmula para completar quadrados (embora tecnicamente exista uma, baseada nas soluções da equação quadrática), e sim um processo.

Quais são os passos para completar quadrados

• Passo 1: Identifique a equação quadrática que você deseja resolver
• Etapa 2: você precisa garantir que a equação esteja totalmente simplificada e que você tenha uma equação da forma ax² + bx + c = 0
• Passo 3: Adicione e subtraia um termo adequado (neste caso, (b/(2a))² para forçar os termos do quadrado de um binômio

A ideia do forçar o aparecimento de um termo da forma (x + "alguma coisa)², que é o objetivo final de completar quadrados.

Por que você usaria equações de segundo grau?

As equações quadráticas aparecem constantemente nas aplicações de álgebra são problemas de palavras. Resolver equações quadráticas é uma habilidade básica que você precisa adquirir.

Então, em áreas como Cálculo, ao computar problemas de maximização e minimização, você precisará ter boa familiaridade com todos os tipos de equações quadráticas.

Exemplo: resolvendo uma equação quadrática

Resolva a seguinte equação quadrática usando a fórmula \(4x^2 + \frac{4}{3}x + 2 = 0\)

Solução: Precisamos resolver a seguinte equação quadrática dada \(\displaystyle 4x^2+\frac{4}{3}x+2=0\).

Para uma equação quadrática da forma \(a x^2 + bx + c = 0\), as raízes são calculadas usando a seguinte fórmula:

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a}\]

Neste caso, temos que a equação que precisamos resolver é \(\displaystyle 4x^2+\frac{4}{3}x+2 = 0\), o que implica que os coeficientes correspondentes são:

\[a = 4\] \[b = \frac{4}{3}\] \[c = 2\]

Primeiro, calcularemos o discriminante para avaliar a natureza das raízes. A discriminação é calculada como:

\[\Delta = b^2 - 4ac = \displaystyle \left( \frac{4}{3}\right)^2 - 4 \cdot \left(4\right)\cdot \left(2\right) = -\frac{272}{9}\]

Como neste caso obtemos o discriminante \(\Delta = \displaystyle -\frac{272}{9} < 0\), que é negativo, sabemos que a equação dada tem duas raízes complexas conjugadas diferentes.

Agora, inserindo esses valores na fórmula das raízes, obtemos:

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a} = \displaystyle \frac{-\frac{4}{3} \pm \sqrt{\left(\frac{4}{3}\right)^2-4\left(4\right)\left(2\right)}}{2\cdot 4} = \displaystyle \frac{-\frac{4}{3} \pm \sqrt{-\frac{272}{9}}}{8}\]

então, descobrimos que:

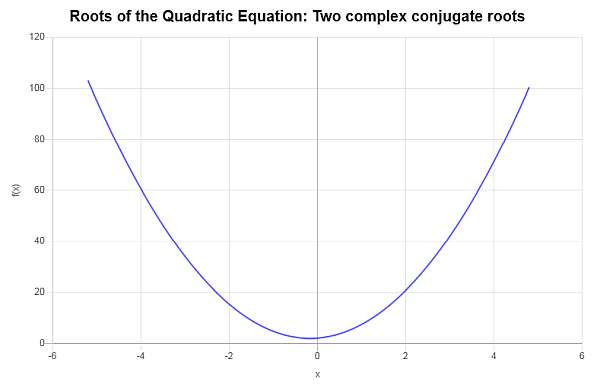
\[\displaystyle x_1 = \frac{-\frac{4}{3} - i \sqrt{\frac{272}{9}}}{8} = -\frac{1}{6} - \frac{1}{6}\sqrt{17} i\] \[\displaystyle x_2 = \frac{-\frac{4}{3} + i \sqrt{\frac{272}{9}}}{8} = -\frac{1}{6} + \frac{1}{6}\sqrt{17} i\]

Portanto, a equação dada \(\displaystyle 4x^2+\frac{4}{3}x+2=0\) tem duas raízes complexas conjugadas diferentes, que são \(x_1 = \displaystyle -\frac{1}{6} - \frac{1}{6}\sqrt{17} i\) e \(x_2 = \displaystyle -\frac{1}{6} + \frac{1}{6}\sqrt{17} i\).

Graficamente:

Exemplo: raiz de uma equação quadrática

Encontre as raízes da seguinte equação quadrática completando quadrados \(2x^2 + \frac{1}{3}x + \frac{1}{72} = 0\)

Solução: Neste caso, temos que a equação que precisamos resolver é \(\displaystyle 2x^2+\frac{1}{3}x+\frac{1}{72} = 0\), o que implica que os coeficientes correspondentes são:

\[a = 2\] \[b = \frac{1}{3}\] \[c = \frac{1}{72}\]

A discriminação é calculada como:

\[\Delta = b^2 - 4ac = \displaystyle \left( \frac{1}{3}\right)^2 - 4 \cdot \left(2\right)\cdot \left(\frac{1}{72}\right) = 0\]

Como neste caso obtemos o discriminante \(\Delta = \displaystyle 0 = 0\), que é zero, sabemos que a equação possui apenas uma raiz real.

Agora, inserindo esses valores na fórmula das raízes, obtemos:

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a} = \displaystyle \frac{-\frac{1}{3} \pm \sqrt{\left(\frac{1}{3}\right)^2-4\left(2\right)\left(\frac{1}{72}\right)}}{2\cdot 2} = \displaystyle \frac{-\frac{1}{3} \pm \sqrt{0}}{4}\]

então, descobrimos que:

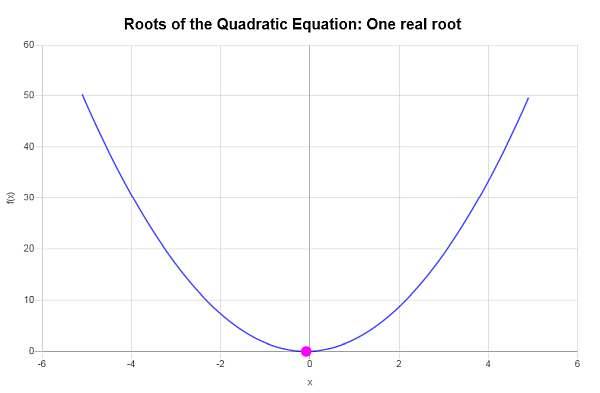
\[x = \displaystyle \frac{-\frac{1}{3}}{4} = \displaystyle -\frac{1}{12}\]

Portanto, a equação dada \(\displaystyle 2x^2+\frac{1}{3}x+\frac{1}{72}=0\) tem apenas uma raiz real, que é \(x = \displaystyle -\frac{1}{12}\).

Graficamente:

Exemplo: raízes do cálculo da equação

Resolva o seguinte: \(3x^2 + \frac{2}{3}x - \frac{4}{3} = 0\)

Solução: Para este exemplo, a equação que precisamos resolver é \(\displaystyle 3x^2+\frac{2}{3}x-\frac{4}{3} = 0\), então os coeficientes correspondentes são:

\[a = 3\] \[b = \frac{2}{3}\] \[c = -\frac{4}{3}\]

Neste caso, o discriminante é calculado como:

\[\Delta = b^2 - 4ac = \displaystyle \left( \frac{2}{3}\right)^2 - 4 \cdot \left(3\right)\cdot \left(-\frac{4}{3}\right) = \frac{148}{9}\]

Como o discriminante é \(\Delta = \displaystyle \frac{148}{9} > 0\), que é positivo, sabemos que a equação terá duas raízes reais diferentes.

Agora, inserindo esses valores na fórmula das raízes, obtemos:

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a} = \displaystyle \frac{-\frac{2}{3} \pm \sqrt{\left(\frac{2}{3}\right)^2-4\left(3\right)\left(-\frac{4}{3}\right)}}{2\cdot 3} = \displaystyle \frac{-\frac{2}{3} \pm \sqrt{\frac{148}{9}}}{6}\]

então, descobrimos que:

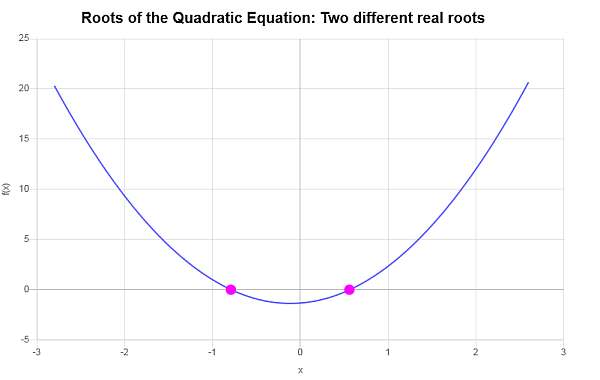
\[ x_1 = -\frac{\frac{2}{3}}{6}-\frac{1}{6}\sqrt{\frac{148}{9}}=-\frac{1}{9}\sqrt{37}-\frac{1}{9} \] \[x_2 = -\frac{\frac{2}{3}}{6}+\frac{1}{6}\sqrt{\frac{148}{9}}=\frac{1}{9}\sqrt{37}-\frac{1}{9}\]

Portanto, a equação dada \(\displaystyle 3x^2+\frac{2}{3}x-\frac{4}{3}=0\) tem duas raízes reais diferentes, que são \(x_1 = \displaystyle -\frac{1}{9}\sqrt{37}-\frac{1}{9}\) e \(x_2 = \displaystyle \frac{1}{9}\sqrt{37}-\frac{1}{9}\).

Graficamente:

Outras calculadoras quadráticas úteis

Como vimos neste tutorial, completando quadrados desempenha um papel fundamental no cálculo de equações quadráticas. Além disso, você pode usar este calculadora discriminante avaliar a natureza das raízes (duas raízes reais, uma raiz real ou duas raízes complexas) sem resolver a equação.

Você também pode usar isso calculadora de vértice para encontrar as coordenadas do vértice de uma equação quadrática, e encontre o eixo de simetria de uma parabola . Além disso, você pode explorar isso fatoração quadrática ferramenta para explorar ainda outra maneira de calcular equações quadráticas.