Estatísticas não paramétricas ou o que fazer quando as premissas para um teste paramétrico falham

A média, a mediana e a moda são as medidas mais comuns de tendência central, usadas para descrever o centro de uma distribuição. Dos três, a média é a mais comumente usada, mas a mediana e a moda também são amplamente usadas.

Precisamos distinguir entre o amostra média, mediana e modo, e seus população homólogos.

Normalmente, nós somos fornecido com uma amostra e precisamos calcular a média da amostra, a mediana da amostra e o modo da amostra. Essas estatísticas são estimadores dos parâmetros populacionais correspondentes.

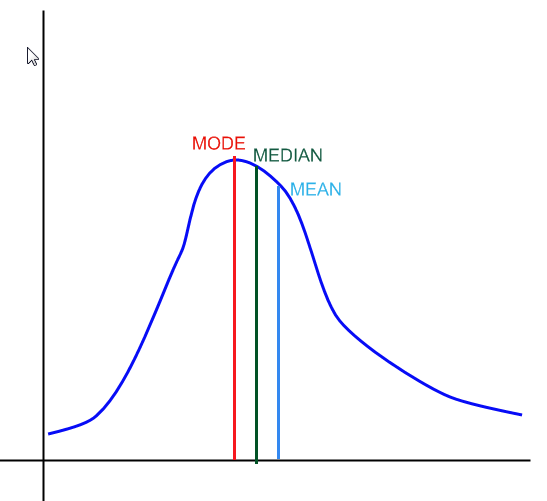
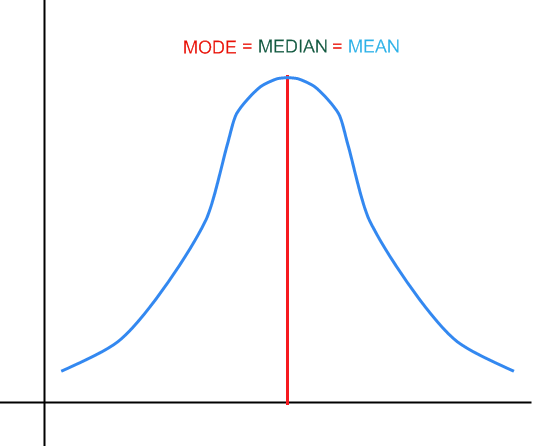
No gráfico acima, você tem um exemplo de como a mediana, o modo e a média seriam em uma distribuição.

O modo corresponde ao valor mais repetido em uma amostra. Em uma distribuição, corresponde ao ponto mais alto na função de densidade, conforme mostrado no gráfico acima.

A mediana, aproximadamente, define o ponto em que 50% da distribuição fica à esquerda e à direita dela.

A média corresponde à média ponderada dos valores que a variável assume e suas probabilidades associadas ($\sum x \cdot p(x)$). Para uma distribuição, essa soma ponderada é uma soma ou uma integral. Para uma amostra, calculamos simplesmente a média dos valores na amostra.

Como calcular a média, mediana e modo para uma determinada amostra

Agora, suponha que recebemos uma amostra $X_1, X_2, ..., X_n$ e queremos calcular o modo, a mediana e a média. Como vamos fazer isso?

• Para o modo: Simples. Apenas encontramos o número que mais se repete. Ex: se tivermos uma amostra 1, 2, 2, 2, 3, 1, 4, o modo é 2, pois 2 é o valor mais repetido (é repetido 3 vezes)

• Para a mediana: Este cálculo é um pouco mais complicado. Pegue sua amostra $X_1, X_2, ..., X_n$ e o primeiro passo é reorganizá-la em ordem crescente. Portanto, assuma que $\hat X_1, \hat X_2, ..., \hat X_n$ é a amostra após reordená-la dos valores mais baixos para os mais altos.

Agora, vamos calcular a posição da mediana na amostra em ordem crescente. Para o tamanho da amostra $n$, calculamos $P = 0.5 (n+1)$.

Se este valor for um inteiro, então descobrimos que a mediana é o valor em P ^º posição na amostra em ordem crescente.

Se este valor NÃO for inteiro, então encontramos $P_L$ e $P_U$ que são os inteiros mais próximos à esquerda e à direita de $P$. (Ex: se $P = 10.2$, então $P_L = 10$ e $P_U = 11$).

Então, a mediana é a média dos valores que estão nas posições $P_L$ ^º e $P_U$ ^º na amostra em ordem crescente. Não se preocupe, vamos praticar isso com um exemplo.

• Para a média: Simples também. A média da amostra é calculada usando uma fórmula

\[\displaystyle \frac{1}{n}\sum_{i=1}^n X_i\]

EXEMPLO 1

Encontre a média, mediana e moda para a seguinte amostra:

28, 36, 43, 30, 15, 19, 46, 36, 34, 38, 42, 29, 37, 35, 39, 39, 30, 39, 36, 38, 30, 41, 42, 46, 40, 33, 30, 40, 43, 12 42, 39, 30, 35, 38, 41, 30, 37, 40, 30, 30, 35, 39, 37, 42, 42, 37, 38, 32, 51

RESPONDA:

A tabela a seguir mostra os cálculos calculados para calcular a média

	Dados
	28
	36
	43
	30
	15
	19
	46
	36
	34
	38
	42
	29
	37
	35
	39
	39
	30
	39
	36
	38
	30
	41
	42
	46
	40
	33
	30
	40
	43
	12
	42
	39
	30
	35
	38
	41
	30
	37
	40
	30
	30
	35
	39
	37
	42
	42
	37
	38
	32
	51

Soma =	1791
Média =	35,82

A média da amostra é, portanto,

\[\bar{X}=\frac{1}{n}\sum{{{X}_{i}}}=\frac{1791}{50}=35.82\]

Agora, para a mediana, a tabela a seguir mostra os dados em ordem crescente:

Dados (em ordem crescente)
12
15
19
28
29
30
30
30
30
30
30
30
30
32
33
34
35
35
35
36
36
36
37
37
37
37
38
38
38
38
39
39
39
39
39
40
40
40
41
41
42
42
42
42
42
43
43
46
46
51

Nesse caso, a posição da mediana é P = 0,5 * (50 + 1) = 25,5, então ${{P}_{L}}=25$ e ${{P}_{U}}=26$. O valor na posição 25 ^º nos dados em ordem crescente é 37, e o valor na posição 26 é 37 também. A mediana é então

\[Median=\frac{{37}+{37}}{2}=37\]

O modo, que é o valor mais repetido, é 30.

O que é maior, a média, a mediana ou a moda?

Essa é uma pergunta que surge com frequência. Em termos gerais, não existe uma resposta para todas as distribuições. Ou seja, a resposta depende da distribuição.

Para uma distribuição simétrica, temos :

\[\Large \text{Mode} = \text{Median} = \text{Mean} \]

Graficamente:

Média, mediana e modo para uma distribuição simétrica

Para uma distribuição inclinada à direita, temos :

\[\Large \text{Mode} \le \text{Median} \le \text{Mean} \]

Graficamente:

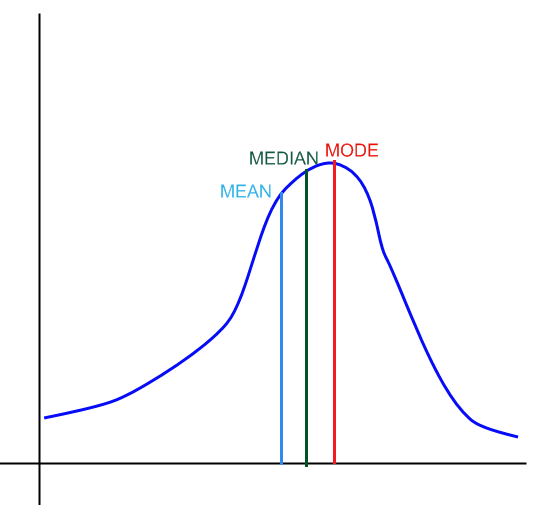
Para uma distribuição inclinada para a esquerda, temos :

\[\Large \text{Mean} \le \text{Median} \le \text{Mode} \]

Graficamente:

Mediana, média e modo para uma distribuição enviesada para a esquerda

Mais sobre a média, mediana e modo

A mediana, a média and the mode are popular popular used in all a part in Statística. Representam medidas de centro, que procuram um valor representativo da amostra.

Correcção do nível de corte, usaríamos uma medida diferente de centro.

• Para dados nominais, entrega o modo.

• Para dados ordinais, não quantitativos, transferência o modo, bem como a medida do centro.

• Para dados quantitativos ordinais, efetua a mediana ou a média como medida do centro.

• Para dados de intervalo e razão, distribuição a média (ou a mediana se a distribuição para muito inclinada) como a medida do centro.

Formulários

A média, a mediana e a moda são as medidas de centro mais comumente usadas. A média e a mediana são usados para dados quantitativos e o modo é usado para dados categóricos.

Para dados quantitativos, normalmente se usaria a média. Com uma ressalva: a média é muito sensível a valores discrepantes. Isso significa que um valor discrepante (valor legítimo ou erro de digitação) pode fazer uma diferença drástica no valor da média.

Nesses casos, quando há outliers ou a distribuição é bastante distorcida, é preferível usar a mediana como a medida mais precisa do centro, porque a média fica distorcida por skewness ou outliers.

Um exemplo disso é quando são coletadas para avaliar a renda dos entrevistados. Se tomarmos uma amostra de 100 pessoas e descobrirmos que 99 delas ganham $ 10.000 por ano e 1 pessoa ganha $ 100 milhões por ano, a renda média dessa amostra seria (10.000 * 99 + 1 * 100.000.000) / 100 = $ 1.009. 900,00. Então, em média, todo mundo ganha $ 1.009.900,00, então você poderia imaginar que esta amostra deve vir de uma área muito rica, mas não é o caso: é apenas um valor discrepante que distorce fortemente a média. De fato, neste caso, a mediana é $ 10.000, que é um valor de centro muito mais representativo para esta amostra.

Calculadoras Relacionadas

Se você precisar ver soluções passo a passo para o cálculo da média e outras medidas de tendência central, dê uma olhada calculadora de estatísticas descritivas . Você também pode achar útil nosso Calculadora de resumo de 5 números .