Método de substituição de integração
O Método de Substituição de Integração ou Integração por Método de Substituição é uma técnica inteligente e intuitiva usada para resolver integrais, e desempenha um papel crucial no dever de resolver integrais, junto com o Integração por partes e decomposição de frações parciais método.
A integração pode ser uma operação difícil às vezes e temos apenas algumas ferramentas disponíveis para prosseguir com ela.
Naturalmente, o cálculo da integral indefinida para algumas funções elementares básicas (como polinômios, potências, funções trigonométricas elementares, etc.) é muito simples.
Mas a questão é como proceder com o cálculo da integral indefinida (ou primitiva) para funções mais complexas ou para a combinação algébrica de funções.
Voce esta pronto para o rock?? Eu sou, então me siga.
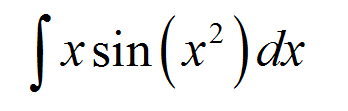
Como funciona o método de substituição?
O método de integração por substituição funciona identificando um "bloco" que contém a variável de integração, de forma que a derivada desse bloco também possa ser encontrada dentro da integral. Esse método também é comumente chamado de método de substituição em u.
Se a estrutura da integral permitir, este "bloco" torna-se na verdade uma nova variável de integração, se tudo correr bem, e a integral torna-se seriamente simplificada.
Isso sempre funciona? Não. Ou dito de outra forma, você sempre pode fazer uma substituição, mas nem sempre vai convertê-la em uma integral mais fácil.
Por que tentar esse método? Bem, porque funciona com frequência. E é normalmente o primeiro truque que você deve tentar se precisar resolver uma integral que não seja trivial.
Deixe-nos colocar algumas etapas a serem seguidas se você precisar aplicar este método:
PASSO 1:
Examine a função que você está integrando e procure um "bloco", ou seja, uma função de \(x\) que aparece uma ou mais vezes na função que você está integrando.
PASSO 2:
O "bloco" que você está procurando precisa ter uma propriedade muito específica: a derivada do bloco precisa aparecer uma vez e apenas uma vez na função que está sendo integrada.
ETAPA 3:
Se as etapas anteriores foram bem-sucedidas, você pode usar o "bloco" como a nova variável e pode substituir a variável e o diferencial pela nova variável, e a integral que você está resolvendo agora se torna muito mais simples.
Nota técnica : Normalmente tento manter todas as explicações simples e tento evitar detalhes técnicos. Nesse caso, terei que dar a explicação técnica para o método de substituição, para não deixar as coisas muito informais com a ideia do "bloco".
Se você não gosta de detalhes técnicos, pode pular para a próxima seção, onde verá os exemplos.
Portanto, a idéia é integrar uma determinada função \(f(x)\). Portanto, precisamos encontrar:
\[\int f(x) \, dx\]Digamos que a função \(f(x)\) não seja qualquer função, e tenha uma certa estrutura específica, especificamente
\[f(x) = g(h(x))h'(x)\]e suponha que haja uma função \(G(x)\) de modo que \(G'(x) = g(x)\) (então \(G\) é a antiderivada de \(g\)). Então, nós entendemos
\[\int f(x) \, dx = \int g(h(x))h'(x) \, dx = G(h(x)) + C\]Por que é que??? Bem, simples: por definição, uma antiderivada é uma função para que, ao diferenciá-la, você obtenha a função que está integrando.
Neste caso, se você diferenciar \( G(h(x)) \), obterá
\[\displaystyle \frac{dG(h(x)}{dx} = G\,'(h(x))h'(x) = g(h(x))h'(x)\]pela Regra da Corrente ..... e shazam! você o tem. Eu disse que não era tão difícil.
Exemplos dos métodos de substituição
A melhor maneira de aprender a integrar é praticando. Algumas pessoas vão se alegrar em olhar as provas, mas a maioria das pessoas vai querer ver as coisas na prática.
Portanto, vamos entrar em questões práticas.
EXEMPLO 1
Encontre a seguinte integral indefinida:
\[\int x \sin(x^2)\,dx\]RESPONDA:
De acordo com a Etapa 1, estamos procurando um bloco, um bloco muito específico. Se você olhar para o integral, a variável de integração é \(x\).
Há muitas tentativas e erros, potencialmente, ao usar essa técnica. Digamos que consideremos o seguinte bloco:
\[u = x^2\]Sabemos que este bloco é bom porque a derivada dele é \(u' = 2x\), que aparece na integral.
Mas então você diz "Eu vejo o \(x\), mas não vejo o 2". Bem, não há necessidade de ficar tenso. Podemos fazer um truque. Observe aquilo
\[\displaystyle \int x \sin(x^2)\,dx = \frac{1}{2}\int 2x \sin(x^2)\,dx\]Quem é você, Mandrake, o Mágico ??? Piadas à parte, esse pequeno truque funciona. Então, a substituição do bloco é
\[u = x^2\] \[du = 2x \, dx\](a notação de \(du = 2x \, dx\) é permissiva e tecnicamente incorreta, mas tem uma base sólida, então tenha paciência). Portanto, fazer essa substituição transformar a integral em
\[\displaystyle \int x \sin(x^2)\,dx = \frac{1}{2}\int 2x \sin(x^2)\,dx \] \[\displaystyle = \frac{1}{2}\int \sin(u)\,du \] \[\displaystyle = -\frac{1}{2} \cos(u) + C \] \[\displaystyle = -\frac{1}{2} \cos(x^2) + C \]Assim, uma vez que você mudou para a nova variável \(u\), a integral tornou-se uma integral mais fácil de resolver de \(\sin(u)\). Depois de resolvê-lo, você DEVE se lembrar de voltar à variável original.
EXEMPLO 2
Agora, vamos passar para um exemplo um pouco mais complicado. Calcule a integral indefinida
\[\int e^{x+e^x} \,dx\]usando o método de substituição em u.
RESPONDA:
O que é isso que você diz ??? Bem, não é tão difícil. Observe que a integral indefinida pode ser reescrita como:
\[\int e^{x+e^x} \,dx = \int e^x e^{e^x} \,dx \]Então, agora que você vê a nova forma da função que está integrando, pode criar um "bloco" ou "substituição em u" ??
Lembre-se, não tenha vergonha de fazer tentativa e erro. Se algo não funcionar, tente outra coisa. E se você tentasse \(u = e^x\)?
A derivada do bloco é \(u' = e^x\), que é encontrada uma vez na função original. Além disso:
\[u = e^x\] \[du = e^x \, dx\]Então, temos:
\[\large \int e^{x+e^x} \,dx = \int e^x e^{e^x} \,dx \] \[\large = \int e^{e^x} e^x \,dx \] \[\large = \int e^{u} \,du \] \[\large = e^{u} + C\] \[\large = e^{e^x} + C\]Mais sobre integração por substituição
Vamos enfrentá-lo: a integração pode ser difícil. Muito difícil. Algumas funções não muito complicadas (pelo menos pelo que parece) deram aos matemáticos um tempo terrivelmente difícil de lidar.
Algumas outras funções não muito complicadas (pelo menos pelo que parece) simplesmente não podem ser resolvidas por métodos elementares.
Portanto, é melhor você acreditar que a integração pode ser uma provação difícil. Então você tem que ir preparado.
Uma das ferramentas mais fáceis e uma técnica muito comumente usada é a técnica de integração por substituição. Sim, é usado porque aparece com frequência em testes ou trabalhos de casa.
Mas trapaceamos um pouco. Na realidade, integrais que possuem a estrutura certa para serem resolvidas pela técnica de substituição são muito específicas. A razão de você ver muitos exemplos disso é porque são funções muito específicas que devem funcionar para serem integradas a essa técnica.
Mas deixe-me ser franco: se você tem um programa de software projetado para gerar funções aleatórias, e ele gera uma para você, as chances de você conseguir usar a técnica de substituição são mínimas.
Ainda assim, é uma pequena técnica de integração poderosa que funciona para uma classe muito específica de integrais.
Qual é a técnica de substituição em u?
A substituição 𝘶 com integrais indefinidos é apenas outro nome para o método de substituição. É chamado de "substituição 𝘶" porque o bloco usado é denominado \(u\), então a nova variável será u.
Definitivamente, esse não é um bom nome, porque o nome que você escolhe para o seu bloco é completamente irrelevante para o processo de cálculo da integral. Você pode chamar o bloco (e sua nova variável) de \(z\) e não faria diferença.