A Eliminação Gaussiana é um processo realizado em matrizes que visa colocar uma matriz em forma escalonada . Ter uma matriz nessa forma ajuda enormemente a resolver equações matriciais com muita facilidade.

Tecnicamente, o processo de realizar a eliminação gaussiana consiste em encontrar uma coluna com um pivô (que é a gíria extravagante para um elemento diferente de zero) que nos permite eliminar todos os elementos abaixo do pivô.

Este processo de encontrar pivôs e eliminar nos permite colocar uma matriz na forma escalonada, e a forma como o processo ocorre é tal que ao girar você adiciona uma nova coluna à forma escalonada, e você não 'arruina' o escalão de você fizeram até a etapa anterior. Linda se você me perguntar.

O termo "forma escalonada" que é obtido usando a eliminação gaussiana torna-se claro ao olhar para a matriz acima, onde os elementos diferentes de zero da matriz têm essa estrutura escalonada, conforme mostrado pela linha vermelha.

A matemática por trás da rotação e eliminação gaussiana

Não vamos entrar muito técnico nisso, só vamos tentar que vocês entendam a motivação e a mecânica desse tipo de eliminação.

A ideia é obter uma matriz \(A\), de dimensão \(m \times n\) (isto é, ela tem \(m\) linhas e \(n\) colunas) em uma forma diferente que seja mais fácil de resolver equações.

Mais especificamente, para uma matriz \(m\times n\) \(A\), e um vetor \(m\times 1\) \(b\), precisamos encontrar um vetor \(n\times 1\) \(x\) de modo que

Você pode pensar, "isso é tão fácil, nós apenas multiplicamos cada lado por \(A^{-1}\) da esquerda" para obtermos:

....Não tão rápido! Isso só funciona quando a matriz \(A\) é invertível. Para começar, a matriz \(A\) tem que ser uma matriz quadrada, e então, seu determinante precisa ser diferente de zero. Mas você não pode multiplicar pelo inverso para matrizes não quadradas. Então, como você faz isso?

Você precisa TRANSFORMAR a equação em uma que seja mais fácil de resolver.

Especificamente, matrizes em forma escalonada são matrizes que levam a equações fáceis de resolver (mais sobre isso mais tarde).

Usando Matrizes Elementares

Em primeiro lugar, faremos uma observação crucial. Se tivermos uma solução da equação da matriz \(Ax = b\), e \(E\) for uma matriz invertível, então \(x\) também será uma solução de \((EA)x = Eb\) e vice-versa.

Em outras palavras, as equações matriciais

e

são equivalentes, para uma matriz invertível \(E\). O que queremos dizer com que as equações são equivalentes? Queremos dizer que as equações têm as mesmas soluções.

Então, o que vamos fazer é começar com \(Ax = b\) e, através da multiplicação por matrizes invertíveis \(E\), chegaremos a uma equação de matriz equivalente que é muito mais fácil de resolver .

Digamos que possamos encontrar uma lista de matrizes invertíveis \(E_1, E_2, ..., E_n\) e multiplicarmos (da esquerda) a equação da matriz original para transformá-la em uma equação equivalente, como:

onde \(E_n \cdots E_2 \cdot E_1 \cdot A = \tilde A\) e \(E_n \cdots E_2 \cdot E_1 \cdot A = \tilde b\).

Nosso objetivo é cuidadosamente escolher as matrizes invertíveis \(E_1, E_2, ..., E_n\) de modo que \(\tilde A\) esteja em forma escalonada.

Por que é que? Porque se \(\tilde A\) está na forma escalonada, resolver a equação da matriz \(\tilde A x = \tilde b\) é muito mais fácil, e já sabemos que \(\tilde A x = \tilde b\) tem as mesmas soluções que \(A x = b\)

EXEMPLO 1

Vamos ver por que resolver uma equação de matriz é muito mais fácil quando você a tem em forma de escalão. Primeiro imagine que você tem a seguinte matriz e vetor:

e você deseja resolver \(Ax = b\). Como seria o sistema de equações? O sistema \(Ax = b\) seria semelhante

Como se parece? Bem, não tão legal. Você precisaria começar a fazer malabarismos com as equações. Existem abordagens mais ou menos sistemáticas para resolver isso usando coisas como eliminação e tal, mas é pelo menos complicado.

Agora, por outro lado, imagine que você tem a seguinte matriz e vetor:

e você deseja resolver \(\tilde A x = \tilde b\). Nesse caso, a matriz \(\tilde A\) está em forma escalonada. Como seria o sistema de equações? O sistema \(\tilde A x = \tilde b\) seria semelhante

Como está este aqui? Bem, não muito pobre.

Na verdade, se começarmos diretamente da terceira equação, teremos que \(x_3 = -1\) diretamente. Então, a partir da segunda equação, \(x_2 = -1 + x_3 = -1 + (-1) = -2\). E da primeira equação, \(x_1 = x_2 + x_3 -1 = -2 + (-1) - 1 = -4\). Então, sem qualquer fuzz, descobrimos que:

Portanto, neste caso, o sistema é resolvido de forma trivial.

Para sistemas associados a matrizes em forma de escalão, é fácil voltar da última equação para a primeira equação, para obter as soluções.

Como escolher as matrizes invertíveis corretas

Agora que sabemos que trabalhar com matrizes em forma escalonada torna realmente muito mais fácil resolver equações matriciais, devemos estar nos perguntando quais são as matrizes invertíveis \(E_1, E_2, ..., E_n\) que farão \(\tilde A\) em forma escalonada.

Como funciona a eliminação de Gauss?

Curiosamente, não é difícil encontrar essas matrizes \(E_1, E_2, ..., E_n\), que serão chamadas de matrizes elementares.

Passo 1 : Observe a primeira coluna, se tiver um valor diferente de zero, esse será o seu pivô. Se a primeira linha da primeira coluna for diferente de zero, use-a como pivô. Caso contrário, encontre uma linha que tenha um valor diferente de zero e permute essa linha e a primeira linha.

Então, você encontra um pivô e, potencialmente, precisa fazer uma permutação de linha (que na verdade é representada pela multiplicação por uma certa matriz invertível)

Passo 2 : Assim que tiver um pivô, elimine todos os elementos da coluna atual, abaixo do pivô.

Isso é feito multiplicando a linha do pivô por uma certa constante e adicionando isso a uma linha abaixo do pivô, de modo que o elemento na mesma coluna do pivô seja zerado.

etapa 3 : Uma vez que todos os elementos abaixo do pivô foram zerados por meio de operações de linha apropriadas (que por acaso são representadas pela operação de uma matriz invertível), vá para a próxima coluna, próxima linha, e procure um pivô na linha abaixo da linha do pivô anterior e faça o mesmo procedimento.

Passo 4 : Repita até esgotar as colunas ou até que a matriz esteja em forma escalonada.

EXEMPLO 2

Usando pivot e eliminação de Gauss, resolva o seguinte sistema:

RESPONDA:

Em primeiro lugar, a matriz associada \(A\) e o vetor \(b\) são:

A matriz aumentada \([A|b]\) é

Para resolver o sistema, precisamos fazer a eliminação gaussiana. Escolhemos o primeiro pivô, começando com a primeira coluna. O elemento na primeira linha da primeira coluna é 1, que é diferente de zero e, em seguida, é usado como um pivô. Usamos esse pivô (1) para eliminar todos os elementos abaixo dele:

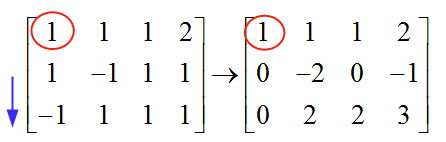
A mecânica de eliminação dos elementos abaixo do pivô é simples. Nesse caso, para eliminar o "1" que está abaixo do pivô, subtraio os elementos da linha 1 aos elementos da linha 2. Assim, formo um zero sob o pivô.

Da mesma forma, para eliminar o "-1" que está na linha 3, adiciono os elementos da linha 1 aos elementos da linha 3. Dessa forma, formo um zero sob o pivô da linha 3.

Veremos que essas operações de linha são obtidas multiplicando-se pela matriz invertível, portanto, temos sistemas equivalentes ao fazer isso.

Agora, indo para a próxima linha, próxima coluna, encontramos um "-2", que é diferente de zero e, portanto, é usado como nosso pivô. Para eliminar o valor abaixo deste pivô, adicionamos à linha 3 os valores da linha 2:

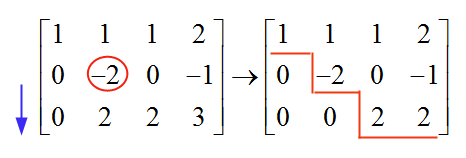
e agora paramos, porque a matriz resultante já está em forma de escalão. Agora voltamos para resolver o sistema: