Desigualdades de valor absoluto
Desigualdades de valor absoluto são desigualdades em que há um ou mais valor absoluto . Vamos lembrar que uma desigualdade é quase como uma equação, mas em vez do sinal "=", temos "≤" ou "≥".
Essa diferença faz com que o conjunto de soluções seja tipicamente uma região, como para a maioria das desigualdades. E o fato de haver valores absolutos envolvidos indica certo tratamento especial para sua resolução.
Neste tutorial, vamos nos concentrar nas habilidades específicas necessárias para a resolução deste tipo de desigualdade que contém um ou mais valores absolutos. Além disso, assumiremos que uma ou duas variáveis, \(x\) e / ou \(y\) estão envolvidas na desigualdade.
O que é uma desigualdade de valor absoluto?
Para o propósito desta análise, consideraremos uma desigualdade de valor absoluto como uma desigualdade envolvendo uma ou duas variáveis, com pelo menos um valor absoluto.
Por exemplo, abaixo temos uma desigualdade de valor absoluto com duas variáveis \(x\) e \(y\):
\[|3x+2y-1| \ge 1\]Ou também, poderíamos ter a seguinte desigualdade de valor absoluto com apenas uma variável:
\[|3x-1| \le 2\]Para os nossos propósitos, e para o propósito das técnicas utilizadas para a sua resolução, trataremos de ambos os tipos de desigualdades (uma e duas variáveis)
Como resolver desigualdades de valor absoluto?
Ao resolver equações ou desigualdades, não existe realmente uma solução mágica que resolve tudo. Cada problema é diferente e pode ter suas peculiaridades.
O melhor que podemos fazer é fornecer uma série de etapas que o ajudarão no processo de solução de uma desigualdade.
Passo 1:
Para cada absoluto, determine as regiões nas quais o argumento do valor absoluto é negativo e onde não é negativo.
Passo 2:
Se houver apenas um valor absoluto na desigualdade, resolva-o em ambas as áreas (onde o argumento do valor absoluto é negativo e onde não é negativo).
Etapa 3:
Se houver mais de um valor absoluto na desigualdade, você precisará cruzar todas as regiões para obter um conjunto de partições menores. Em cada partição, você precisa saber EXATAMENTE o sinal de cada argumento. Então, resolva a desigualdade em todas as áreas.
Passo 4:
Depois de obter a solução da peça que está em cada uma das áreas, a solução final é a simples união dessas soluções de peça.
Em palavras simples: você precisa descobrir as regiões onde você sabe exatamente o sinal do argumento dos valores absolutos (para que você possa se livrar deles).
Alguns exemplos devem esclarecer essas etapas.
EXEMPLO 1
Resolva a seguinte desigualdade
\[| 2x + 4y - 1 | \ge 2\]RESPONDA:
Para resolver a desigualdade, precisamos usar as etapas que foram especificadas acima.
Passo 1: Há apenas um valor absoluto, portanto, precisamos determinar se o argumento é negativo ou não negativo. Portanto, precisamos resolver primeiro:
\[2x + 4y - 1 \ge 0\]Existem várias estratégias para resolver o acima, mas a mais fácil é primeiro resolver a equação
\[2x + 4y - 1 = 0\]o que significa que \(4y = -2x + 1\) ou o mesmo que \(y = -\frac{1}{2}x + \frac{1}{4}\), que corresponde a uma linha com inclinação \(m = -\frac{1}{2}\) e interceptação y \(n = \frac{1}{4}\).
Agora, para cuidar de \(2x + 4y - 1 \ge 0\) testamos se o ponto \((0,0)\) satisfaz ou não a desigualdade:
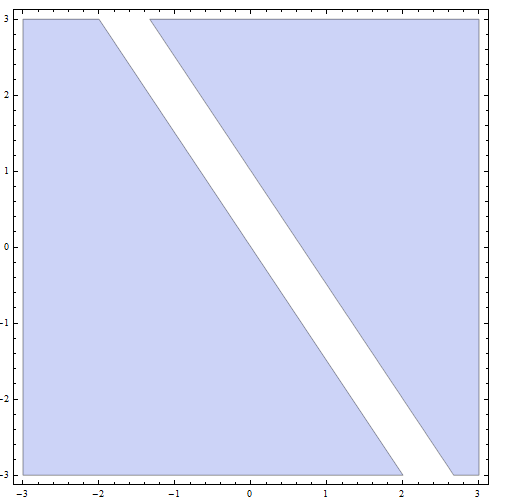
\[2(0) + 4(0) - 1 = -1 < 0\]Portanto, \((0,0)\) satisfaz ou não a desigualdade. A conclusão é que a linha com inclinação \(m = -\frac{1}{2}\) e interceptação y \(n = \frac{1}{4}\) divide o plano em duas regiões:
Para os pontos abaixo da linha (chamamos esta região 1, \(R_1\)), obtemos que \(2x + 4y - 1 < 0\)
Para os pontos acima da linha, incluindo a própria linha (chamamos esta região 2, \(R_2\)), obtemos que \(2x + 4y - 1 \ge 0\)
Por que isso é importante? Por que nos damos todo esse trabalho? Porque em \(R_1\), obtemos isso desde \( 2x + 4y - 1 < 0\), então \(| 2x + 4y - 1 | = -(2x + 4y - 1) \). Da mesma forma, em \(R_2\), obtemos isso desde \( 2x + 4y - 1 \ge 0\), então \(| 2x + 4y - 1 | = 2x + 4y - 1 \).
Passo 2: Agora precisamos resolver a desigualdade na região 1, \(R_1\) :
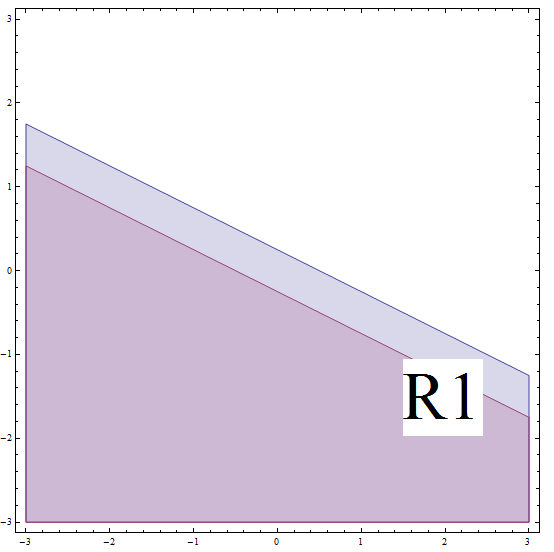
\[| 2x + 4y - 1 | \ge 2\] \[\Rightarrow -(2x + 4y - 1) \ge 2\] \[\Rightarrow 2x + 4y - 1 \le -2 \text{ (multiplying by (-1) changes the direction of the inequality)}\] \[\Rightarrow 2x + 4y \le -1\] \[\Rightarrow 4y \le -2x - 1\] \[\Rightarrow y \le -\frac{1}{2}x - \frac{1}{4} \]Isso corresponde a todos os pontos abaixo ou na linha com inclinação \(m = -\frac{1}{2}\) e interceptação y \(n = -\frac{1}{4}\). Mas não se esqueça de que você está em \(R_1\), e esta linha que encontramos ABAIXO do limite de \(R_1\) (veja o gráfico abaixo).
Para esclarecer, uma vez que presumimos que estamos em \(R_1\), precisamos ter a linha ABAIXO com inclinação \(m = -\frac{1}{2}\) e interceptação y \(n = \frac{1}{4}\). Sob essa suposição, resolvemos a desigualdade original e também precisamos estar abaixo da linha com inclinação \(m = -\frac{1}{2}\) e interceptação y \(n = -\frac{1}{4}\). Essas duas condições devem acontecer simultaneamente, então temos a interseção das duas regiões.
Então, a solução da peça neste caso corresponde a todos os pontos abaixo ou na linha com inclinação \(m = -\frac{1}{2}\) e interceptação y \(n = -\frac{1}{4}\).
Agora precisamos resolver a desigualdade na região 2, \(R_2\) :
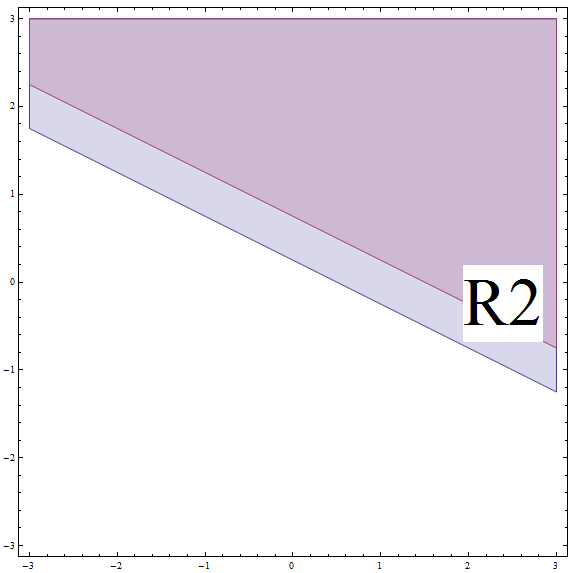
\[| 2x + 4y - 1 | \ge 2\] \[\Rightarrow 2x + 4y - 1 \ge 2\] \[\Rightarrow 2x + 4y \ge 3\] \[\Rightarrow 4y \ge -2x + 3\] \[\Rightarrow y \ge -\frac{1}{2}x + \frac{3}{4} \]Isso corresponde a todos os pontos acima ou na linha com inclinação \(m = -\frac{1}{2}\) e interceptação y \(n = \frac{3}{4}\). Mas não se esqueça de que você está em \(R_2\), e esta linha está ACIMA do limite de\(R_2\) (veja o gráfico abaixo).
Ao encontrar a interseção entre \(R_2\) e a região acima, obtemos que a solução da parte neste caso são todos os pontos acima ou na linha com inclinação \(m = -\frac{1}{2}\) e interceptação y \(n = \frac{3}{4}\).
Passo 4: Agora, a solução final é a união de todas as soluções das partes anteriores: A solução final é todos os pontos ABAIXO ou na linha com inclinação \(m = -\frac{1}{2}\) e interceptação y \(n = -\frac{1}{4}\), MAIS todos os pontos ACIMA ou na linha com inclinação \(m = -\frac{1}{2}\) e interceptar y \(n = \frac{3}{4}\).
Graficamente, temos
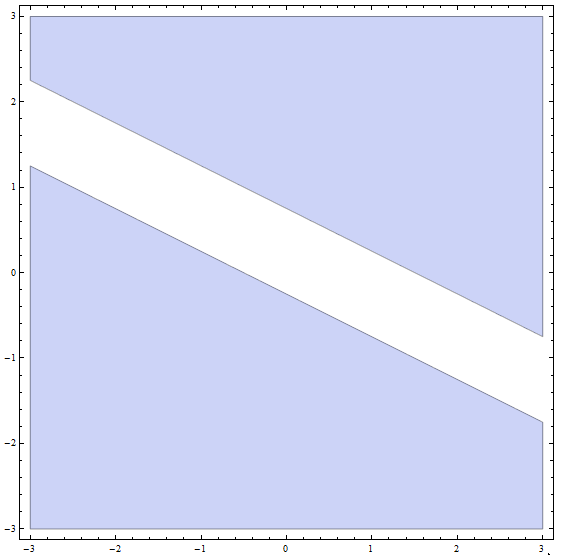
que conclui a resolução da desigualdade.
EXEMPLO 2
Resolva a seguinte desigualdade de valor absoluto duplo
\[| 2x - 1 | \ge |x + 3|\]RESPONDA:
Esta é uma desigualdade de valor absoluto duplo porque existem 2 valores absolutos. Isso significa que encontrar as regiões exigirá um pouco mais de trabalho (relativamente falando).
Passo 1: Para o primeiro valor absoluto, resolvemos:
\[2x- 1 \ge 0\] \[\Rightarrow \,\, 2x \ge 1\] \[\Rightarrow \,\, x \ge \frac{1}{2}\]Então, obtemos \(2x- 1 \ge 0\) em \([\frac{1}{2}, +\infty)\) e \(2x- 1 < 0\) em \((-\infty, \frac{1}{2})\).
Para o segundo valor absoluto, resolvemos:
\[x+3 \ge 0\] \[\Rightarrow \,\, x \ge -3\]Então, obtemos \(x+3 \ge 0\) em \([-3, +\infty)\) e \(x+3 < 0\) em \((-\infty, -3)\).
Então, definimos 4 regiões:
\(R_1 = [\frac{1}{2}, +\infty) \cap [-3, +\infty) = [\frac{1}{2}, +\infty)\). Nesta região temos: \(2x- 1 \ge 0\) AND \(x+3 \ge 0\).
\(R_2 = [\frac{1}{2}, +\infty) \cap (-\infty, -3) = \varnothing\). Nesta região temos: \(2x- 1 \ge 0\) AND \(x+3 < 0\), embora esta região esteja vazia.
\(R_3 = (-\infty, \frac{1}{2}) \cap [-3, +\infty) = [-3, \frac{1}{2})\). Nesta região obtemos: \(2x- 1 < 0\) AND \(x+3 \ge 0\)
\(R_4 = (-\infty, \frac{1}{2}) \cap (-\infty, -3) = (-\infty, -3)\). Nesta região temos: \(2x- 1 < 0\) AND \(x+3 < 0\).
Passo 2: Agora precisamos resolver a desigualdade de valor absoluto duplo em cada uma das quatro regiões:
• Em \(R_1\):
Aqui temos \(2x- 1 \ge 0\) AND \(x+3 \ge 0\) então
\[| 2x - 1 | \ge |x + 3|\] \[\Rightarrow \,\, 2x - 1 \ge x + 3\] \[\Rightarrow \,\, 2x - x \ge 3 - (-1)\] \[\Rightarrow \,\, x \ge 4\]Portanto, para obter a solução da peça, precisamos interceptar \(x \ge 4\), ou \([4, +\infty)\) com \(R_1\).
A solução da parte correspondente é, portanto: \([\frac{1}{2}, +\infty) \cap [4, +\infty) = [4, +\infty)\)
• Em \(R_2\):
Esta solução parcial está vazia (\(\varnothing\)).
• Em \(R_3\):
Aqui temos \(2x- 1 < 0\) AND \(x+3 \ge 0\) então
\[| 2x - 1 | \ge |x + 3|\] \[\Rightarrow \,\, -(2x - 1) \ge x + 3\] \[\Rightarrow \,\, 2x - 1 \le -x - 3\] \[\Rightarrow \,\, 2x - (-x) \le -3 - (-1)\] \[\Rightarrow \,\, 3x \le -2\] \[\Rightarrow \,\, x \le -\frac{2}{3}\]Portanto, para obter essa solução parcial, precisamos cruzar \( x \le -\frac{2}{3}\), ou \( (-\infty, -\frac{2}{3}]\) com \(R_3\).
A solução da parte correspondente é, portanto: \((-\infty, -\frac{2}{3}] \cap [-3, \frac{1}{2}) = [-3, -\frac{2}{3}] \)
• Em \(R_4\):
Aqui temos \(2x- 1 < 0\) AND \(x+3 < 0\) então
\[| 2x - 1 | \ge |x + 3|\] \[\Rightarrow \,\, -(2x - 1) \ge -(x + 3)\] \[\Rightarrow \,\, 2x - 1 \le x + 3\] \[\Rightarrow \,\, 2x - x \le 3 - (-1)\] \[\Rightarrow \,\, x \le 4\]Portanto, para obter essa solução parcial, precisamos cruzar \( x \le 4 \), ou \((-\infty, 4]\) com \(R_4\).
A solução da parte correspondente é, portanto: \((-\infty, -3) \cap (-\infty, 4] = (-\infty, -3) \)
Passo 4:
Finalmente, obtemos a união das soluções das partes, para obter que a solução da desigualdade inicial dada é
Ninguém disse que seria curto, certo? Bem. Não é muito difícil, você só precisa ser sistemático e seguir o plano.
Mais sobre desigualdades com valor absoluto
Por que nos preocupamos com esse tipo de desigualdade? Nós nos importamos porque eles têm aplicações na prática.
Por exemplo, em geometria, as distâncias na linha real precisam ser representadas como um valor absoluto, porque precisa ser não negativo.
Pode-se ter uma determinada situação geométrica em que você precisa encontrar todos os pontos da reta real que estão a uma distância de pelo menos 2 do ponto 3. Tal situação pode ser descrita com a seguinte desigualdade:
\[| x-3 |\ge 2\]Vamos entender a desigualdade acima. O ponto \(x\) é o ponto que queremos satisfazer a desigualdade. A distância de \(x\) ao ponto 3 é representada por \(|x - 3|\).
Então, estamos tentando encontrar os pontos que estão a uma distância de pelo menos 2 do ponto 3, então a distância \(|x - 3|\) precisa ser pelo menos 2, o que explica o \(|x - 3| \ge 2.\)
Este é apenas um tipo de problema de desigualdade de valor absoluto que você pode encontrar na prática.
Você pode encontrar desigualdades de valor absoluto sem solução
Pode apostar. Aqui você tem um \(|2x| < |x|\). É possível que uma desigualdade seja simplesmente inviável como é o caso desta que acabei de apresentar.
Que tal representar graficamente as desigualdades de valor absoluto?
O processo de representá-los graficamente está essencialmente de mãos dadas com o processo de resolvê-los: você precisa encontrar as regiões onde sabe exatamente se os argumentos dos valores absolutos são positivos ou negativos e, em seguida, como desigualdades de valor absoluto tornam- se desigualdades simples, que é gráfico trivialmente. Em seguida, todas as peças das regiões específicas são simplesmente unidas.