Resumo de cinco números

mais sobre isso Calculadora de resumo de 5 números para você entender melhor o passo a passo dos resultados fornecidos por esta calculadora.

Como você calcula o resumo de 5 números?

A primeira coisa que você precisa saber é quais são as partes de um resumo de 5 números, que é uma das técnicas mais comuns utilizadas em estatística descritiva.

O resumo de cinco números é um conjunto de 5 estatísticas descritivas diferentes que lhe darão uma visão rápida e precisa da distribuição dos dados da amostra que você está analisando.

Seu cálculo é um processo de várias etapas, que envolve a obtenção de 5 informações. Na verdade, para um conjunto de amostra de dados, o resumo de cinco números é um conjunto de 5 números que fornece uma percepção rápida sobre a forma de uma distribuição. O resumo de cinco números inclui o mínimo , o primeiro quartil $(Q_1)$, Médio , o terceiro quartil $(Q_3)$ e o máximo .

O Resumo de cinco números pode informar sobre o centro e a distribuição da distribuição da amostra, bem como o tipo de distorção (se houver) e possíveis discrepâncias.

Etapas necessárias para o cálculo do resumo de 5 números

Como encontrá-lo dependerá de como você deseja proceder e, você verá, há diferentes maneiras de calculá-lo.

1. Se você usar nossa calculadora, basta fornecer os dados da amostra e a calculadora fará o trabalho, mostrando todos os passos.
2. Se você usar o Excel, precisará calcular cada um dos componentes do resumo de 5 números separadamente, pois não existe uma função específica para obtê-los de uma vez. Uma pequena coisa sobre o Excel é que ele tende a usar um método simplificado demais para calcular quartis
3. Se você fizer isso manualmente, precisará classificar os dados em ordem crescente. Então, o primeiro número será o mínimo e o último será o máximo. A mediana e os quartis são calculados usando uma convenção de interpolação para a posição dos valores na lista.

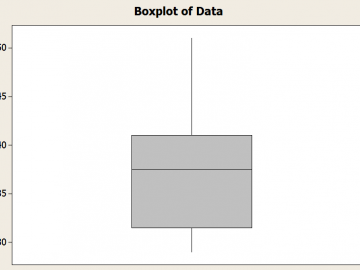
O gráfico de caixa de resumo de 5 números

Como estão o resumo de 5 números e o gráfico de caixa relacionado ?. Bem, é uma relação muito estreita, pois o boxplot é essencialmente construído COM BASE nos 5 números.

Na verdade, os limites inferior e superior da caixa são dados por trimestre do primeiro trimestre do terceiro trimestre , os bigodes são determinados pelo máximo e pelo mínimo (embora haja um limite baseado no valor do AIQ , usando o critério IQR de 1,5 vez)

Calculadoras estatísticas mais descritivas

Você pode, por outro lado, estar interessado em obter uma lista completa de estatísticas descritivas, que inclui as medidas mais comuns de tendência central e desvio. Para fazer isso, você pode seguir nosso passo a passo calculadora estatística descritiva

. Além disso, o resumo de 5 números desempenha um papel crucial na construção do gráfico de caixa , que lhe diz muito sobre a distribuição de determinados dados de amostra, bem como sobre o detecção de valores discrepantes .

Resumindo

O resumo de 5 números é uma coleção de números que ajuda a retratar medidas de tendência central e dispersão de alguns dados de amostra. Os componentes são:

• O mínimo
• O primeiro quartil
• A mediana
• O terceiro quartil
• o máximo

Exemplo de resumo de cinco números:

Pergunta : Considere os seguintes dados de amostra: 1, 1, 2, 3, 4, 4, 2, 3, 2, 1, 2, 3, 4, 5, 6, 6, 6, 2, 10, 11. Calcule os cinco -Resumo de números à mão, mostrando todos os cálculos.

Solução:

Estes são os dados de amostra que foram fornecidos com:

Observação	$X$
1	1
2	1
3	2
4	3
5	4
6	4
7	2
8	3
9	2
10	1
11	2
12	3
13	4
14	5
15	6
16	6
17	6
18	2
19	10
20	11

Estes são os dados de amostra que foram fornecidos com:

Posição	$X$ (Asc. Order)
1	1
2	1
3	1
4	2
5	2
6	2
7	2
8	2
9	3
10	3
11	3
12	4
13	4
14	4
15	5
16	6
17	6
18	6
19	10
20	11

Com base na tabela acima, o mínimo é $\min = 1$ e o máximo é $\max = 11$. Agora a posição do primeiro quartil $Q_1$ é:

$$L_{25} = \frac{25}{100} \times (n+1) = 0.25 \times 21 = 5.25$$

Como $L_{25} = 5.25$ não é um número inteiro, o primeiro quartil $Q_1$ é calculado interpolando entre os valores localizados nas posições $5^{th}$ e $6^{th}$, conforme fórmula abaixo:

$$Q_1 = 2 + (5.25 - 5)\times (2 - 2) = 2$$

Como o tamanho da amostra $n = 20$ é par, temos que $(n+1)/2 = (20+1)/2 = 10.5$ não é um valor inteiro, então a mediana é calculada diretamente encontrando a média dos valores localizados nas posições $10^{th}$ e $11^{th}$, que é:

$$median = \displaystyle \frac{3 + 3}{2} = 3.5$$

Agora a posição do terceiro quartil $Q_3$ é:

$$L_{75} = \frac{75}{100} \times (n+1) = 0.75 \times 21 = 15.75$$

Como $L_{75} = 15.75$ não é um número inteiro, o terceiro quartil $Q_3$ é calculado interpolando entre os valores localizados nas posições $15^{th}$ e $16^{th}$, conforme fórmula abaixo:

$$Q_3 = 5 + (15.75 - 15)\times (6 - 5) = 5.75$$

Portanto, com base nos resultados encontrados acima, obtemos o seguinte resumo de cinco números:

Minimum =	$1$
$Q_1$ =	$2$
Median =	$3.5$
$Q_3$ =	$5.75$
Maximum =	$11$