Gráfico de caixa e bigode
O Box and Whisker Plot, ou também conhecido como Box-plot, é um tipo de representação gráfica de uma amostra, que fornece fácil visualização das principais características da distribuição de uma amostra.
Um gráfico de caixa e bigode fornece a mediana, bem como o primeiro e o terceiro quartis em sua "caixa", e o mínimo e o máximo em "bigode".
Quando o mínimo ou máximo são muito extremos, "aparamos" o bigode e anotamos a existência de um outlier.
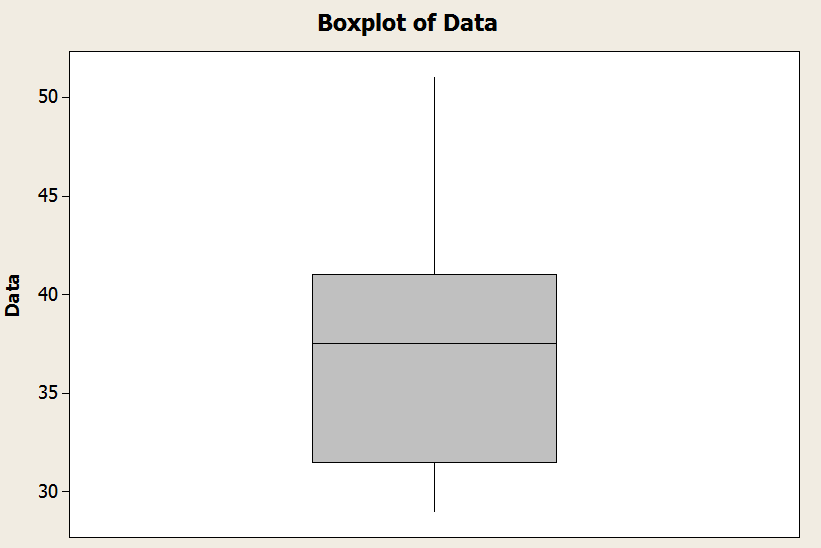
No gráfico acima, você tem um exemplo de como um boxplot se parece: Você tem a "caixa" e os bigodes.
A linha inferior da caixa é definida pelo primeiro quartil (\(Q_1\)).
A linha do meio da caixa é definida pela mediana (\(Q_2\)).
A linha superior da caixa é definida pelo terceiro quartil (\(Q_3\)).
Agora, para os bigodes, há uma regra a seguir: o bigode inferior é definido pelo mínimo da amostra, e o bigode superior é definido pelo máximo da amostra. Isso é feito desde que o tamanho do bigode seja menor que \(1.5 \times IQR\), onde \(IQR\) é o intervalo interquartil, e é definido por \(IQR = Q_3 - Q_1\).
Veja o gráfico de exemplo abaixo.
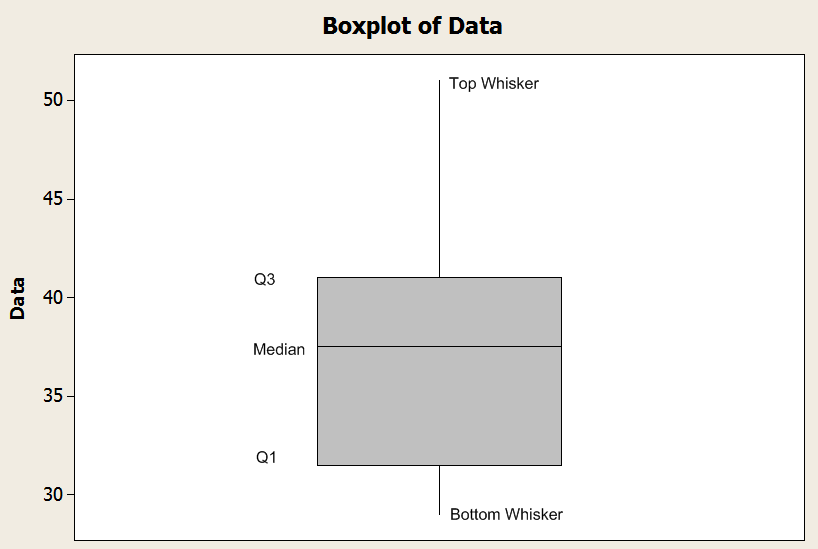
Então, se o mínimo da amostra for maior que \(Q_1 - 1.5 \times IQR\), o bigode inferior é definido pelo mínimo. Caso contrário, é definido por \(Q_1 - 1.5 \times IQR\).
Da mesma forma, se o máximo da amostra for menor que \(Q_3 + 1.5 \times IQR\), então o bigode superior é definido pelo máximo. Caso contrário, é definido por \(Q_3 + 1.5 \times IQR\).
EXEMPLO 1
Construa um gráfico de caixa para o seguinte exemplo:
28, 36, 43, 30, 46, 19, 46, 36, 34, 38, 42, 29, 37, 35, 39, 39, 30, 39, 36, 38, 30, 41, 42, 46, 40, 33, 30, 40, 43, 30, 42, 39, 30, 35, 38, 41, 30, 37, 40, 30, 30, 35, 39, 37, 42, 42, 37, 38, 32, 51
RESPONDA:
Conseguimos que o máximo e o mínimo são
\[\min = 19\] \[\max = 51\]A tabela a seguir mostra os dados em ordem crescente:
|
Dados (em ordem crescente) |
|
19 |
|
28 |
|
29 |
|
30 |
|
30 |
|
30 |
|
30 |
|
30 |
|
30 |
|
30 |
|
30 |
|
30 |
|
32 |
|
33 |
|
34 |
|
35 |
|
35 |
|
35 |
|
36 |
|
36 |
|
36 |
|
37 |
|
37 |
|
37 |
|
37 |
|
38 |
|
38 |
|
38 |
|
38 |
|
39 |
|
39 |
|
39 |
|
39 |
|
39 |
|
40 |
|
40 |
|
40 |
|
41 |
|
41 |
|
42 |
|
42 |
|
42 |
|
42 |
|
42 |
|
43 |
|
43 |
|
46 |
|
46 |
|
46 |
|
51 |
A mediana é então
\[Median=\frac{{37}+{38}}{2}=37.5\]A posição do 25º percentil é
\[{{L}_{25}}=\frac{P}{100}\times \left( n+1 \right)=\frac{25}{100}\times \left( 50+1 \right) = {12.75}\]Então, nós entendemos
\[{{Q}_{1}}={30} +{0.75}\times \left( {32}-{30} \right) = {31.5}\]A posição do 75º percentil é
\[{{L}_{75}}=\frac{P}{100}\times \left( n+1 \right)=\frac{75}{100}\times \left( 50+1 \right) = {38.25}\]Então, nós entendemos
\[{{Q}_{3}}={41}+{0.25}\times \left( {41}-{41} \right) = {41}\]Portanto, o resumo de 5 números é
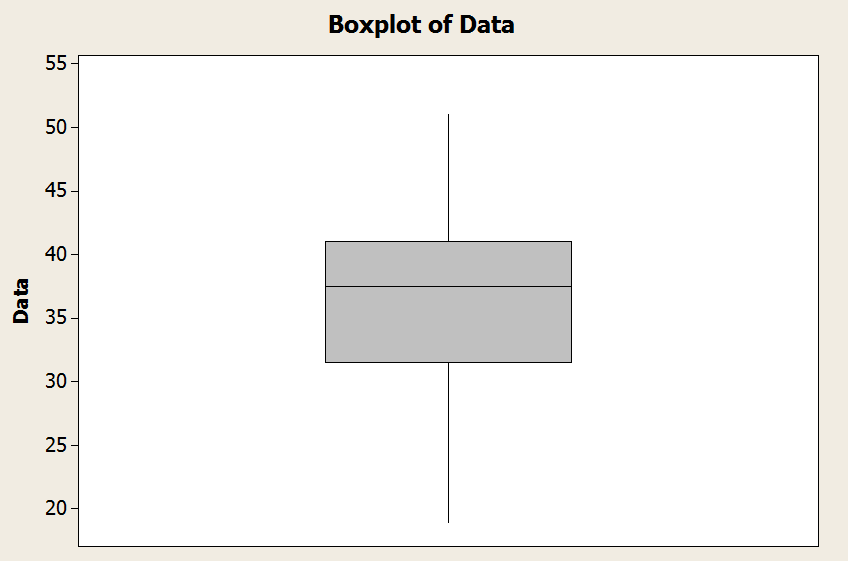
\[\min = 19, Q_1 = 31.5, Q_2 = 37.5, Q_3 = 41, \max = 51\]O intervalo interquartil, neste caso, é \(IQR = Q_3 - Q_1 = 41 - 31.5 = 9.5\). Conseqüentemente,
\(Q_1 - 1.5 \times IQR = 31.5 - 1.5 \times 9.5 = 17.25\)
\(Q_3 + 1.5 \times IQR = 41 + 1.5 \times 9.5 = 55.25\)
Observe que o mínimo é 19 e é maior que \(Q_1 - 1.5 \times IQR = 17.25\). E o máximo é 51, e é inferior a \(Q_3 + 1.5 \times IQR = 55.25\).
Concluímos que o bigode inferior é o mínimo, e o bigode superior é o máximo neste caso. Graficamente
EXEMPLO 2
Encontre o gráfico de caixa para a mesma amostra do exemplo anterior, mas quando você substituir "51" por "81".
RESPONDA:
Conseguimos que o máximo e o mínimo são
\[\min = 19\] \[\max = 81\]A tabela a seguir mostra os dados em ordem crescente:
|
Dados (em ordem crescente) |
|
19 |
|
28 |
|
29 |
|
30 |
|
30 |
|
30 |
|
30 |
|
30 |
|
30 |
|
30 |
|
30 |
|
30 |
|
32 |
|
33 |
|
34 |
|
35 |
|
35 |
|
35 |
|
36 |
|
36 |
|
36 |
|
37 |
|
37 |
|
37 |
|
37 |
|
38 |
|
38 |
|
38 |
|
38 |
|
39 |
|
39 |
|
39 |
|
39 |
|
39 |
|
40 |
|
40 |
|
40 |
|
41 |
|
41 |
|
42 |
|
42 |
|
42 |
|
42 |
|
42 |
|
43 |
|
43 |
|
46 |
|
46 |
|
46 |
|
81 |
A mediana é então
\[Median=\frac{{37}+{38}}{2}=37.5\]A posição do 25º percentil é
\[{{L}_{25}}=\frac{P}{100}\times \left( n+1 \right)=\frac{25}{100}\times \left( 50+1 \right) = {12.75}\]Então, nós entendemos
\[{{Q}_{1}}={30} +{0.75}\times \left( {32}-{30} \right) = {31.5}\]A posição do 75º percentil é
\[{{L}_{75}}=\frac{P}{100}\times \left( n+1 \right)=\frac{75}{100}\times \left( 50+1 \right) = {38.25}\]Então, nós entendemos
\[{{Q}_{3}}={41}+{0.25}\times \left( {41}-{41} \right) = {41}\]Portanto, o resumo de 5 números é
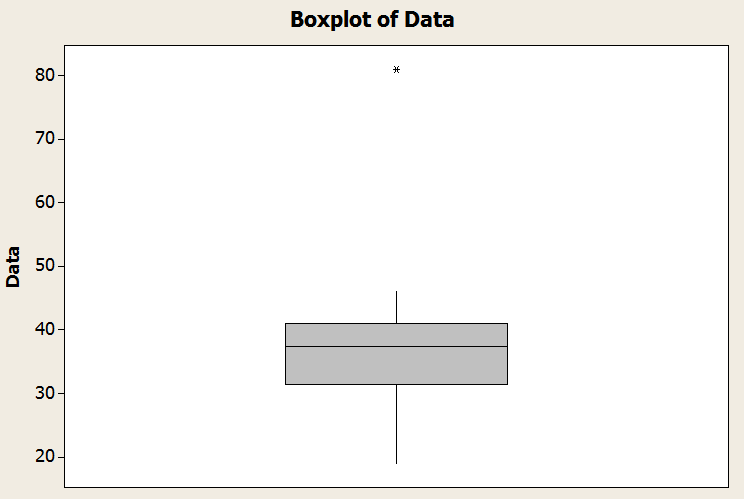
\[\min = 19, Q_1 = 31.5, Q_2 = 37.5, Q_3 = 41, \max = 81\]O intervalo interquartil, neste caso, é \(IQR = Q_3 - Q_1 = 41 - 31.5 = 9.5\). Conseqüentemente,
\(Q_1 - 1.5 \times IQR = 31.5 - 1.5 \times 9.5 = 17.25\)
\(Q_3 + 1.5 \times IQR = 41 + 1.5 \times 9.5 = 55.25\)
Observe que o mínimo é 19 e é maior que \(Q_1 - 1.5 \times IQR = 17.25\). Mas agora o máximo é 81, que excede \(Q_3 + 1.5 \times IQR = 55.25\). Portanto, o valor "81" é um outlier.
Concluímos que o bigode inferior é o mínimo, e o bigode superior é definido por \(Q_3 + 1.5 \times IQR = 55.25\). Graficamente
Mais sobre o Boxplot
A principal questão que as pessoas têm é o que os boxplots dizem a você. O que eles representam. E a resposta é simples: eles fornecem uma representação resumida da distribuição de uma amostra, fornecendo um gráfico esquemático que mostra a posição relativa do Resumo de 5 números .
Dessa forma, você pode procurar outliers , você pode avaliar o grau de assimetria da distribuição e pode escanear rapidamente as regiões com 25%, 50% e 75% da distribuição total.
Diferença entre Box-plot e Histograma
Uma das coisas sobre o gráfico de caixa é que ele fornece informações ligeiramente diferentes das informações fornecidas por um histograma.
Na verdade, o histograma mostra a forma bruta da distribuição, com base nas classes usadas para classificar os valores possíveis da variável aleatória. Por outro lado, o boxplot fornece informações resumidas sobre os quartis e o resumo de 5 números, que diz muito sobre a posição relativa do primeiro e do terceiro quartil em relação à mediana.
Em outras palavras, o boxplot, ao contrário do histograma, apresenta um gráfico que representa um resumo da distribuição , em vez de uma representação bruta. Os únicos valores brutos que entrariam em um boxplot seriam os outliers (se houver).
Formulários
A aplicação mais clássica do gráfico de caixa é para detectar outliers. Por definição, o gráfico de caixa limita o tamanho dos bigodes a 1,5 vezes o intervalo interquartil \((IQR)\) das extremidades da caixa (que são definidas por \(Q_1\) e \(Q_3\).
Portanto, qualquer ponto que ultrapasse o tamanho máximo dos bigodes será anotado no box-plot e será considerado um outlier.
Pratique os conceitos que você aprendeu neste tutorial usando este fabricante de box-plot . Outro criador de gráficos que permitirá ver em um vislumbre as propriedades distributivas da distribuição de uma amostra é este fabricante de histograma , ou isto Criador de plotagem de caule e folha .